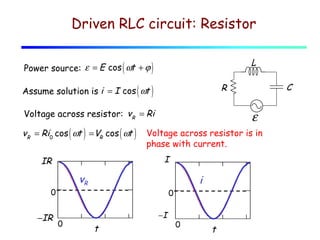
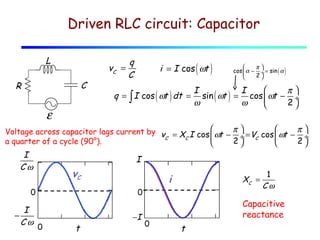
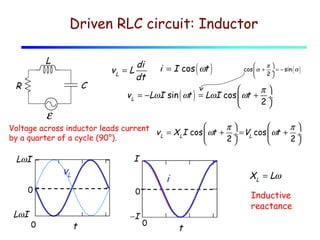
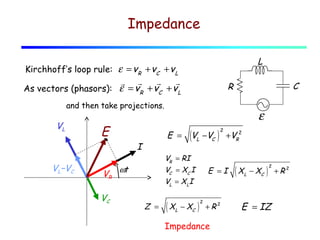
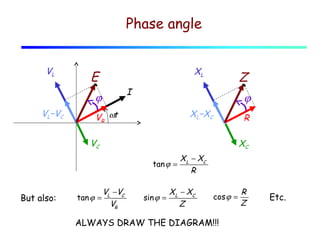
The document discusses AC circuits using phasors to represent voltages and currents. It introduces the concepts of resistive reactance (R), capacitive reactance (XC), and inductive reactance (XL). R causes voltage to be in phase with current, while XC causes voltage to lag current by 90° and XL causes voltage to lead current by 90°. Together, R, XC and XL determine the impedance (Z) and phase angle (φ) of the circuit. The document uses an example of an L-C circuit to show how to calculate the frequency where XC and XL are equal.

1. Lecture 29
AC circuits. Phasors.

2. Driven RLC circuit
Analogy between circuits and SHM:
Circuits
Oscillations.
No energy dissipation.
Oscillations with decreasing
amplitude.
Energy dissipation.
Driven oscillations.
Energy dissipation and supply
Mechanical
LC
Spring/mass (SHM)
RLC
Spring/mass with
damping
RLC with AC
generator
Spring/mass with
damping and driving
force

3. Preview
– Source: ~ produces an oscillating voltage (supplies whatever
current the rest of the circuit “requires”)
– Resistor:
causes a voltage drop when a current flows
through. As soon as the voltage changes, so does the current ⇒
always in phase.
– Capacitor:
resists change in charge Q ⇒ resists change in
voltage. Voltage across capacitor lags behind the current by 90°.
– Inductor:
resists change in magnetic flux ⇒ resists change
in current. Voltage across inductor is ahead of the current by 90˚.

4. AC generator
Generic problem: we are given an AC voltage source that “drives” a circuit
ε = E cos ( ωt )
∼
Supplies a given emf that
depends on time (usually as a
sine of cosine)
Goal: Determine current that flows: i = I cos ( ωt − ϕ )
It is reasonable to expect another sinusoidal function with frequency ω
(and possibly a phase ϕ)
Note: Current must be the same through all elements if they are in series.

5. Driven RLC circuit: Resistor
L
Power source: ε = E cos ( ωt + ϕ )
Voltage across resistor: vR = Ri
vR = Ri0 cos ( ωt ) = VR cos ( ωt )
Voltage across resistor is in
phase with current.
vR
0
−IR
ε
I
IR
i
0
0
−I
t
C
R
Assume solution is i = I cos ( ωt )
0
t

6. Driven RLC circuit: Capacitor
L
vC =
C
R
q
C
i = I cos ( ωt )
q = ∫ I cos ( ωt ) dt =
ε

π
cos  α − ÷ = sin ( α )
2


I
I
π
sin ( ωt ) = cos  ωt − ÷
ω
ω
2

Voltage across capacitor lags current by v = X I cos  ωt − π  = V cos  ωt − π 

÷

÷
C
C
2 C
2
a quarter of a cycle (90°).


r1
x
0,
.. r1
n
I
1
Cω
I
vC
i
0
XC =
0
f( x ) 0
I
−
Cω 10
0
2
t
x
4
6
−I
0
1
Cω
Capacitive
reactance
t

7. Driven RLC circuit: Inductor
L
di
vL = L
dt
C
R

π
cos  α + ÷ = − sin ( α )
2


π
v L = −LωI sin ( ωt ) = LωI cos  ωt + ÷
2

ε
x
i = I cos ( ωt )


π
π
Voltage across inductor leads current
v L = X LI cos  ωt + ÷ = VL cos  ωt + ÷
by a quarter of a cycle (90°).
2
2


r1
0,
n
.. r1
LωI1
I
vL
0
f( x ) 0
LωI
1
0
XL = Lω
i
0
0
2
t
x
4
6
−I
Inductive
reactance
0
t

8. Mnemotechnic trick
Introducing…
ELI the ICE man
For L:
For C :
ε leads I
I leads ε

9. Phasors
ε = E cos ( ωt + ϕ )
vR = VR cos ( ωt )

π
vC = VC cos  ωt − ÷
2


π
v L = VL cos  ωt + ÷
2

i = I cos ( ωt )
This looks intimidating…
VR = RI
1
Cω
VR = XC I
XC =
VL = X LI
X L = Lω
VL
VR
I
ωt
We can make it easier if we think
that these are components of
vectors called phasors.
Magnitude of the phasors:
VR = RI
VC = XC I
VL = X LI
The entire thing rotates CCW.
VC
Real voltages = horizontal
projections of the phasors.

10. Impedance
L
Kirchhoff’s loop rule: ε = vR + vC + v L
r
r
r r
As vectors (phasors): ε = vR + vC + v L
C
R
and then take projections.
VL
VL−VC
E
VR
VC
ε
E =
I
(VL −VC
VR = RI
VC = XC I
VL = X LI
ωt
Z =
( XL − XC
)
2
+VR2
E =I
)
2
+R2
Impedance
( XL − XC
)
2
E = IZ
+R2

11. Phase angle
VL
XL
E
I
ϕ
VL−VC
Z
ϕ
XL−XC
VR ωt
R
VC
XC
tan ϕ =
But also:
tan ϕ =
VL −VC
VR
sin ϕ =
X L − XC
R
X L − XC
Z
cos ϕ =
ALWAYS DRAW THE DIAGRAM!!!
R
Z
Etc.

12. What is reactance?
It’s something like frequency-dependent resistance…
XC =
1
Cω
For high ω, XC ~ 0
⇒ Capacitor looks like a wire (“short”)
For low ω, XC →∞
⇒ Capacitor looks like a break
XL = Lω
For low ω, XL ~ 0
⇒ Capacitor looks like a wire (“short”)
For high ω, XL →∞
⇒ Capacitor looks like a break
" XR " = R
No frequency dependence.

13. In-class example: Equal reactance
For what angular frequency will a 35 mH inductor and a 25 μF
capacitor have the same reactance, and what is the value of the
reactance at this frequency?
A. 9.3×10-4 s-1,
25 Ω
B. 9.3×10 s ,
37 Ω
-4
C. 1100 s-1,
D. 1100 s ,
-1
-1
25 Ω
ω=
37 Ω
E. None of the above
(
XC = X L
)(
1
LC
⇔
=
( 35 × 10
)
1
1
XC =
=
= 37 Ω
−6
3
−1
Cω
25 × 10 F 1.1 × 10 s
)(
−3
)(
H 25 × 10 −6 F
)
= 1.1 × 103 s −1
It’s the natural frequency of the circuit!
X L = Lω = 35 × 10 −3 H 1.1 × 103 s −1 = 37 Ω
(
1
= Lω
Cω
1
)
At this frequency,
ϕ=0