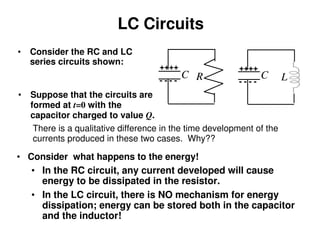
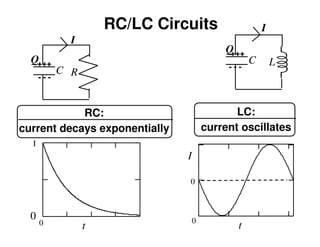
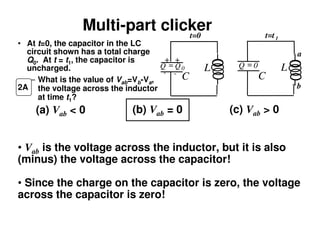
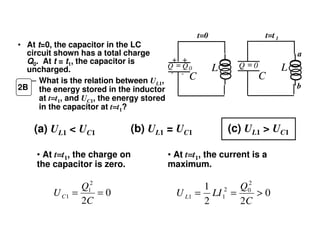
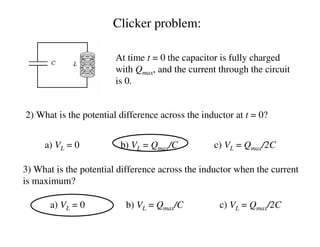
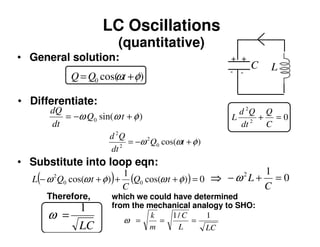
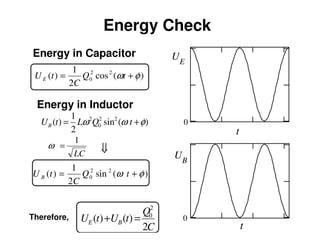
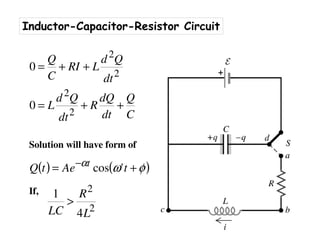
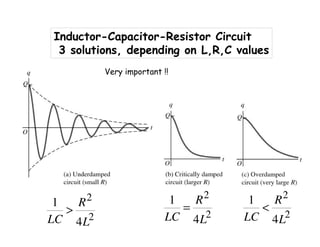
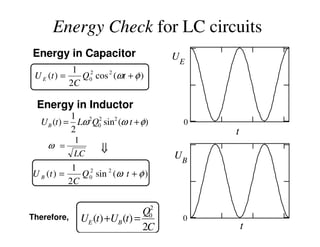
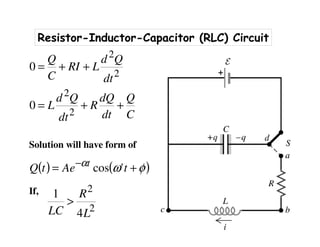
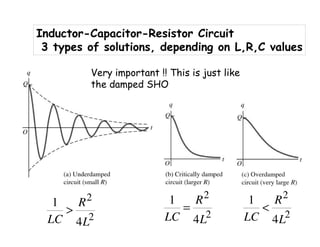
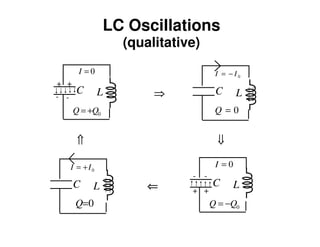
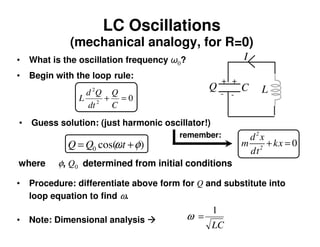
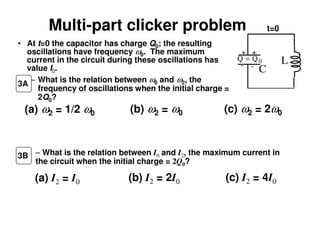
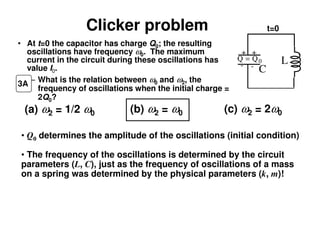
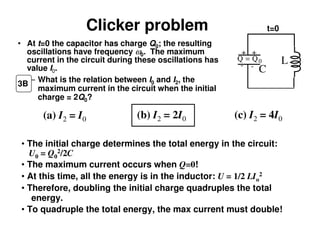
1) The document discusses LC circuits, noting a qualitative difference in how currents develop in RC versus LC circuits. In an LC circuit, energy can be stored in both the inductor and capacitor without dissipation, unlike an RC circuit where energy is dissipated in the resistor. 2) An LC circuit with an initially charged capacitor will undergo oscillations of the current, not exponential decay as in an RC circuit. The frequency of these oscillations is determined to be 1/sqrt(LC) from the equations for the energy stored in each component. 3) Increasing the inductance decreases the oscillation frequency in an LC circuit, while increasing the capacitance also decreases the frequency, according to the governing equation relating the

1. Physics -272 Lecture 19
LC Circuits
RLC Circuits
AC Circuit Theory

2. LC Circuits
• Consider the RC and LC
series circuits shown:
• Suppose that the circuits are
formed at t=0 with the
capacitor charged to value Q.
There is a qualitative difference in the time development of the
currents produced in these two cases. Why??
• Consider what happens to the energy!
• In the RC circuit, any current developed will cause
energy to be dissipated in the resistor.
• In the LC circuit, there is NO mechanism for energy
dissipation; energy can be stored both in the capacitor
and the inductor!
LCC R
++++
- - - -
++++
- - - -

3. Energy in the Electric
and Magnetic Fields
21
2
U LI=
2
magnetic
0
1
2
B
u
µ
=… energy density ...
Energy stored in an inductor ….
B
Energy stored in a capacitor ...
21
2
U C V=
2
electric 0
1
2
u Eε=… energy density ...
+++ +++
- - - - - -
E

4. RC/LC Circuits
RC:
current decays exponentially
C R
0
t
I
0
I
Q+++
- - -
LC
LC:
current oscillates
I
0
0
t
I
Q+++
- - -

5. LC Oscillations
(qualitative)
⇒⇒⇒⇒
⇐⇐⇐⇐
⇓⇓⇓⇓
LC
+ +
- -
0=I
0QQ +=
LC
+ +
- -
0=I
0QQ −=
LC
0II −=
0=Q
⇑⇑⇑⇑
LC
0II +=
0=Q

6. Multi-part Clicker
• At t=0, the capacitor in the LC
circuit shown has a total charge
Q0. At t = t1, the capacitor is
uncharged.
– What is the value of Vab=Vb-Va,
the voltage across the inductor
at time t1?
(a) Vab < 0 (b) Vab = 0 (c) Vab > 0
(a) UL1 < UC1 (b) UL1 = UC1 (c) UL1 > UC1
– What is the relation between UL1, the energy stored in the
inductor at t=t1, and UC1, the energy stored in the capacitor at
t=t1?
2B
2A
L
C
L
C
+ +
- -
Q = 0Q Q= 0
t=0 t=t1
a
b

7. Multi-part clicker
• At t=0, the capacitor in the LC
circuit shown has a total charge
Q0. At t = t1, the capacitor is
uncharged.
– What is the value of Vab=Vb-Va,
the voltage across the inductor
at time t1?
(a) Vab < 0 (b) Vab = 0 (c) Vab > 0
2A
• Vab is the voltage across the inductor, but it is also
(minus) the voltage across the capacitor!
• Since the charge on the capacitor is zero, the voltage
across the capacitor is zero!
L
C
L
C
+ +
- -
Q = 0Q Q= 0
t=0 t=t1
a
b

8. • At t=0, the capacitor in the LC
circuit shown has a total charge
Q0. At t = t1, the capacitor is
uncharged.
(a) UL1 < UC1 (b) UL1 = UC1 (c) UL1 > UC1
2B
• At t=t1, the charge on
the capacitor is zero.
0
2
2
1
1 ==
C
Q
UC 0
22
1 2
02
11 >==
C
Q
LIU L
• At t=t1, the current is a
maximum.
L
C
L
C
+ +
- -
Q = 0Q Q= 0
t=0 t=t1
a
b
– What is the relation between UL1,
the energy stored in the inductor
at t=t1, and UC1, the energy stored
in the capacitor at t=t1?

9. At time t = 0 the capacitor is fully charged
with Qmax, and the current through the circuit
is 0.
2) What is the potential difference across the inductor at t = 0?
a) VL = 0 b) VL = Qmax/C c) VL = Qmax/2C
3) What is the potential difference across the inductor when the current
is maximum?
a) VL = 0 b) VL = Qmax/C c) VL = Qmax/2C
Clicker problem:

10. LC Oscillations
(mechanical analogy, for R=0)
• Guess solution: (just harmonic oscillator!)
where φ, Q0 determined from initial conditions
• Procedure: differentiate above form for Q and substitute into
loop equation to find ω.
• Note: Dimensional analysis
LC
+ +
- -
I
Q
• What is the oscillation frequency ω0?
• Begin with the loop rule:
02
2
=+
C
Q
dt
Qd
L
)cos(0 φω += tQQ
remember:
0
2
2
d x
m kx
dt
+ =
LC
1
=ω

11. LC Oscillations
(quantitative)
• General solution:
)cos(0 φω += tQQ
LC
+ +
- -
02
2
=+
C
Q
dt
Qd
L
• Differentiate:
)sin(0 φωω +−= tQ
dt
dQ
)cos(0
2
2
2
φωω +−= tQ
dt
Qd
• Substitute into loop eqn:
⇒⇒⇒⇒( ) ( ) 0)cos(
1
)cos( 00
2
=+++− φωφωω tQ
C
tQL 0
12
=+−
C
Lω
Therefore,
LC
1
=ω
LCL
C
m
k 1/1
===ω
which we could have determined
from the mechanical analogy to SHO:

12. Multi-part clicker problem
• At t=0 the capacitor has charge Q0; the resulting
oscillations have frequency ω0. The maximum
current in the circuit during these oscillations has
value I0.
– What is the relation between ω0 and ω2, the
frequency of oscillations when the initial charge =
2Q0?
(a) ω2 = 1/2 ω0 (b) ω2 = ω0 (c) ω2 = 2ω0
(a) I2 = I0 (b) I2 = 2I0 (c) I2 = 4I0
– What is the relation between I0 and I2, the maximum current in
the circuit when the initial charge = 2Q0?
3B
3A
L
C
+ +
- -
Q Q= 0
t=0

13. Clicker problem
• At t=0 the capacitor has charge Q0; the resulting
oscillations have frequency ω0. The maximum
current in the circuit during these oscillations has
value I0.
– What is the relation between ω0 and ω2, the
frequency of oscillations when the initial charge =
2Q0?
(a) ω2 = 1/2 ω0 (b) ω2 = ω0 (c) ω2 = 2ω0
3A
• Q0 determines the amplitude of the oscillations (initial condition)
• The frequency of the oscillations is determined by the circuit
parameters (L, C), just as the frequency of oscillations of a mass
on a spring was determined by the physical parameters (k, m)!
L
C
+ +
- -
Q Q= 0
t=0

14. Clicker problem
• At t=0 the capacitor has charge Q0; the resulting
oscillations have frequency ω0. The maximum
current in the circuit during these oscillations has
value I0.
– What is the relation between I0 and I2, the
maximum current in the circuit when the initial
charge = 2Q0?
(a) I2 = I0 (b) I2 = 2I0 (c) I2 = 4I0
3B
• The initial charge determines the total energy in the circuit:
U0 = Q0
2/2C
• The maximum current occurs when Q=0!
• At this time, all the energy is in the inductor: U = 1/2 LIo
2
• Therefore, doubling the initial charge quadruples the total
energy.
• To quadruple the total energy, the max current must double!
L
C
+ +
- -
Q Q= 0
t=0

15. The current in a LC circuit is a
sinusoidal oscillation, with
frequency ω.
5) If the inductance of the circuit is increased, what will happen
to the frequency ω?
a) increase b) decrease c) doesn’t change
6) If the capacitance of the circuit is increased, what will
happen to the frequency?
a) increase b) decrease c) doesn’t change
Clicker question:

16. LC Oscillations
Energy Check
• The other unknowns ( Q0, φφφφ ) are found from the initial
conditions. E.g., in our original example we assumed initial
values for the charge (Qi) and current (0). For these values:
Q0 = Qi, φφφφ = 0.
• Question: Does this solution conserve energy?
)(cos
2
1)(
2
1
)( 22
0
2
φω +== tQ
CC
tQ
tUE
)(sin
2
1
)(
2
1
)( 22
0
22
φωω +== tQLtLitUB
• Oscillation frequency has been found from the
loop equation. LC
1
=ω

17. UE
t
0
Energy Check
UB
0
t
Energy in Capacitor
)(cos
2
1
)( 22
0 φω += tQ
C
tU E
⇒⇒⇒⇒
Energy in Inductor
)(sin
2
1
)( 22
0
2
φωω += tQLtUB
LC
1
=ω
)(sin
2
1
)( 22
0 φω += tQ
C
tU B
C
Q
tUtU BE
2
)()(
2
0
=+Therefore,

18. Inductor-Capacitor Circuits
Solving a LC circuit problem; Suppose ωωωω=1/sqrt(LC)=3 and
given the initial conditions,
Solve find Q0 and φφφφ0000,,,, to get complete solution using,
and we find,
( )
( ) AtI
CtQ
150
50
==
==
( ) ( )
( ) ( ) ( )0000
00
0sin30sin150
0cos50
φφω
φ
+−=+−===
+===
QQtI
QtQ
( ) ( ) ( )[ ]
o
45,
35
15
tan.
25,cossin
3
15
5
00
0
2
00
2
0
22
0
2
2
−=





⋅
−=
==+=





−+
φφ
φφ
inv
QQQ

19. Remember harmonic oscillators !!
( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( )( )
( ) ( ) ( )tBtAtQ
ttQtQ
tQtQ
tQtQ
ωω
φωφω
φω
φω
sincos
sinsincoscos
sin
cos
000
10
00
+=
−=
+=
+=
The following are all equally valid solutions

20. Inductor-Capacitor-Resistor Circuit
C
Q
dt
dQ
R
dt
Qd
L
dt
Qd
LRI
C
Q
++=
++=
2
2
2
2
0
0
Solution will have form of
If,
( ) ( )φωα += −
tAetQ t
'cos
2
2
4
1
L
R
LC
>

21. Inductor-Capacitor-Resistor Circuit
3 solutions, depending on L,R,C values
2
2
4
1
L
R
LC
> 2
2
4
1
L
R
LC
=
2
2
4
1
L
R
LC
<
Very important !!

22. Inductor-Capacitor-Resistor Circuit
Solving for all the terms
( ) ( )
2
2
2
2
2
4
1
'and
2
4
1
cos
'cos
L
R
LCL
R
t
L
R
LC
Ae
tAetQ
t
L
R
t
−==








+−=
+=






−
−
ωα
φ
φωα
Solution for underdamped circuit;
2
2
4
1
L
R
LC
>
For other solutions, use starting form, solve for λλλλ and λλλλ′′′′,
( ) tt
BeAetQ 'λλ −−
+=

23. Application of magnetic induction: “smart”
traffic lights
Traffic light in California
Another version with
two loops

24. Application of magnetic induction
Magnetic energy from ignition coil is used to fire
the automotive spark plug.
Mechanical
ignition in a
car

25. The current in a LC circuit is a
sinusoidal oscillation, with
frequency ω.
I) If the inductance of the circuit is increased, what will happen
to the frequency ω?
a) increases b) decreases c) doesn’t change
II) If the capacitance of the circuit is increased, what will
happen to the frequency?
a) increases b) decreases c) doesn’t change
2 –part Clicker question:
1
LC
ω =

26. UE
t
0
Energy Check for LC circuits
UB
0
t
Energy in Capacitor
)(cos
2
1
)( 22
0 φω += tQ
C
tU E
⇒⇒⇒⇒
Energy in Inductor
)(sin
2
1
)( 22
0
2
φωω += tQLtUB
LC
1
=ω
)(sin
2
1
)( 22
0 φω += tQ
C
tU B
C
Q
tUtU BE
2
)()(
2
0
=+Therefore,

27. Inductor-Capacitor (LC) Circuit Example
Solving a LC circuit problem; Suppose ωωωω=1/sqrt(LC)=3 and
given the initial conditions,
Solve find Q0 and φφφφ0000,,,, to get complete solution using,
and we find,
( )
( ) AtI
CtQ
150
50
==
==
( ) ( )
( ) ( ) ( )0000
00
0sin30sin150
0cos50
φφω
φ
+−=+−===
+===
QQtI
QtQ
( ) ( ) ( )[ ]
o
45,
35
15
tan.
25,cossin
3
15
5
00
0
2
00
2
0
22
0
2
2
−=





⋅
−=
==+=





−+
φφ
φφ
inv
QQQ

28. Remember harmonic oscillators !!
( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( )( )
( ) ( ) ( )tBtAtQ
ttQtQ
tQtQ
tQtQ
ωω
φωφω
φω
φω
sincos
sinsincoscos
sin
cos
000
10
00
+=
−=
+=
+=
The following are all equally valid solutions

29. Resistor-Inductor-Capacitor (RLC) Circuit
C
Q
dt
dQ
R
dt
Qd
L
dt
Qd
LRI
C
Q
++=
++=
2
2
2
2
0
0
Solution will have form of
If,
( ) ( )φωα += −
tAetQ t
'cos
2
2
4
1
L
R
LC
>

30. Inductor-Capacitor-Resistor Circuit
3 types of solutions, depending on L,R,C values
2
2
4
1
L
R
LC
> 2
2
4
1
L
R
LC
=
2
2
4
1
L
R
LC
<
Very important !! This is just like
the damped SHO

31. Inductor-Capacitor-Resistor Circuit
( ) ( )
2
2
2
2
2
4
1
'and
2
4
1
cos
'cos
L
R
LCL
R
t
L
R
LC
Ae
tAetQ
t
L
R
t
−==








+−=
+=






−
−
ωα
φ
φωα
Solution for underdamped circuit;
2
2
4
1
L
R
LC
>
For other solutions, use starting form, solve for λλλλ and λλλλ′′′′,
( ) tt
BeAetQ 'λλ −−
+=

32. Alternating Currents (Chap 31)
We next study circuits where the battery is replaced by
a sinusoidal voltage or current source.
or
The circuit symbol is,
An example of an LRC circuit connected to sinusoidal source is,
( )tVtv ωcos)( 0= ( )tIti ωcos)( 0=
Important:
I(t) is same throughout – just
like the DC case.

33. Alternating Currents (Chap 31.1)
Since the currents & voltages are sinusoidal, their values change
over time and their average values are zero.
A more useful description of sinusoidal currents and voltages are
given by considering the average of the square of this quantities.
We define the RMS (root mean square), which is the
square root of the average of ,
( )( )2
0
2
cos)( tIti ω=
( )( ) ( )( )
2
2cos1
2
1
cos)(
2
02
0
2
0
2 I
tItIti =+== ωω
2
)( 02 I
tiIRMS ==
2
)( 02 V
tvVRMS ==Similarly:

34. Alternating Currents ; Phasors
A convenient method to describe currents and voltages in AC
circuits is “Phasors”. Since currents and voltages in circuits with
capacitors & inductors have different phase relations, we introduce
a phasor diagram. For a current,
We can represent this by a vector
rotating about the origin. The angle
of the vector is given by ωt and the
magnitude of the current is its
projection on the X-axis.
If we plot simultaneously currents &
voltages of different components we
can display relative phases .
( )tIi ωcos=
Note this method is equivalent to imaginary numbers approach
where we take the real part (x-axis projection) for the magnitude

35. Alternating Currents: Resistor in AC circuit
A resistor connected to an AC source will have the voltage, vR, and
the current across the resistor has the same phase. We can represent the
current phasor and the voltage phasor with the same angle.
( ) ( )RtIiRtVv RR ωω coscos ===
Phasors are rotating 2 dimensional vectors
IRVR =and (just like DC case)

36. Resistor in AC circuit; I & V versus ωωωω t
I(t)=Icos(ωωωωt)
V(t)=RIcos(ωωωωt)
ωωωωt →→→→
a b c d e f
NB: for a resistor voltage is in phase with current

37. Alternating Currents: Capacitor in AC circuit
In a capacitor connected to an AC current source the voltage
lags behind the current by 90 degree. We can draw the current
phasor and the voltage phasor behind the current by 90 degrees.
( )cos tI
dt
dq
i ω==
( )t
C
I
idt
CC
q
v ω
ω
sin
1
=== ∫Find voltage:
( )t
I
q ω
ω
sin=





=
C
IVMAX
ω
1

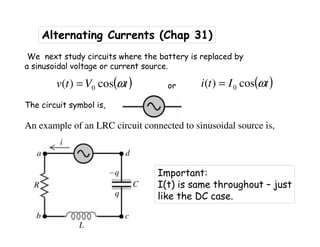
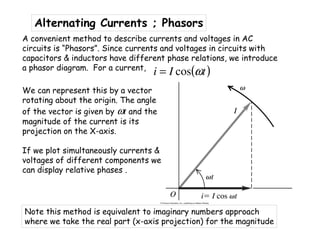
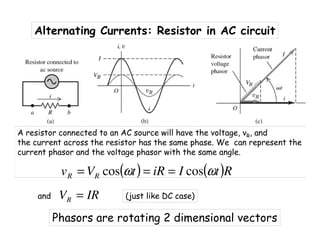
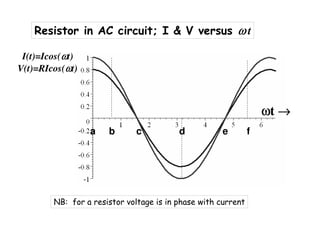
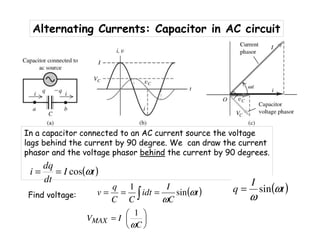
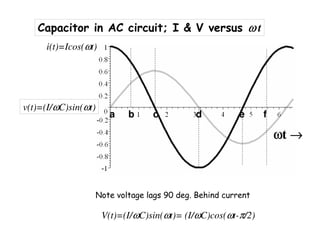
38. Alternating Currents ; Capacitor in AC circuit
We stated that voltage lags by 90 deg., so equivalent solution is
( ) [ ]
t
C
I
tt
C
I
t
C
I
v
ω
ω
ωω
ω
ω
ω
sin
90sinsin90coscos90cos
=
+=−=
1
C
XC
ω
=We define the capacitive reactance, XC, as
C
MAX
cap XI
C
I
C
I
V =





==
ωω
1
Like: VR = IR
But frequency dependent

39. i(t)=Icos(ωt)
v(t)=(I/ωC)sin(ωt)
a b c d e f
Note voltage lags 90 deg. Behind current
Capacitor in AC circuit; I & V versus ωωωω t
V(t)=(I/ωC)sin(ωt)= (I/ωC)cos(ωt-π/2)
ωωωωt →→→→

40. Alternating Currents: Inductor in AC circuit
In an inductor connected to an AC current source, the voltage will
lead the current by 90 degrees. We can draw the current
phasor and the voltage phasor ahead of the current by 90 degrees.
( ) ( )tIL
dt
di
LVtIi ωωω sinandcos −===
ωILVMAX =
Define inductive reactance, XL, as LX L ω=
( ) L
MAX
ind XILILIV === ωω
Like: VR = IR
But frequency dependnt

41. i(t)=Icos(ωωωωt)
v(t)= - ILωωωωsin(ωωωωt)
Inductor in AC circuit; I & V versus ωωωω t
a b c d e f
Draw phasor diagram for each point
Note voltage is 90 deg. ahead of current
v(t)=ILωωωω sin(ωωωωt)= ILωωωω cos(ωωωωt + ππππ/2)
ωωωωt →→→→

42. AC summary
leadsIXLωL-VLsin ωtI cosωtinductor
lagsIXC1/ωCVC sin ωtI cosωtcapacitor
in phaseIRRVR cos ωtI cosωtresistor
PhasorVXv(t)i(t)