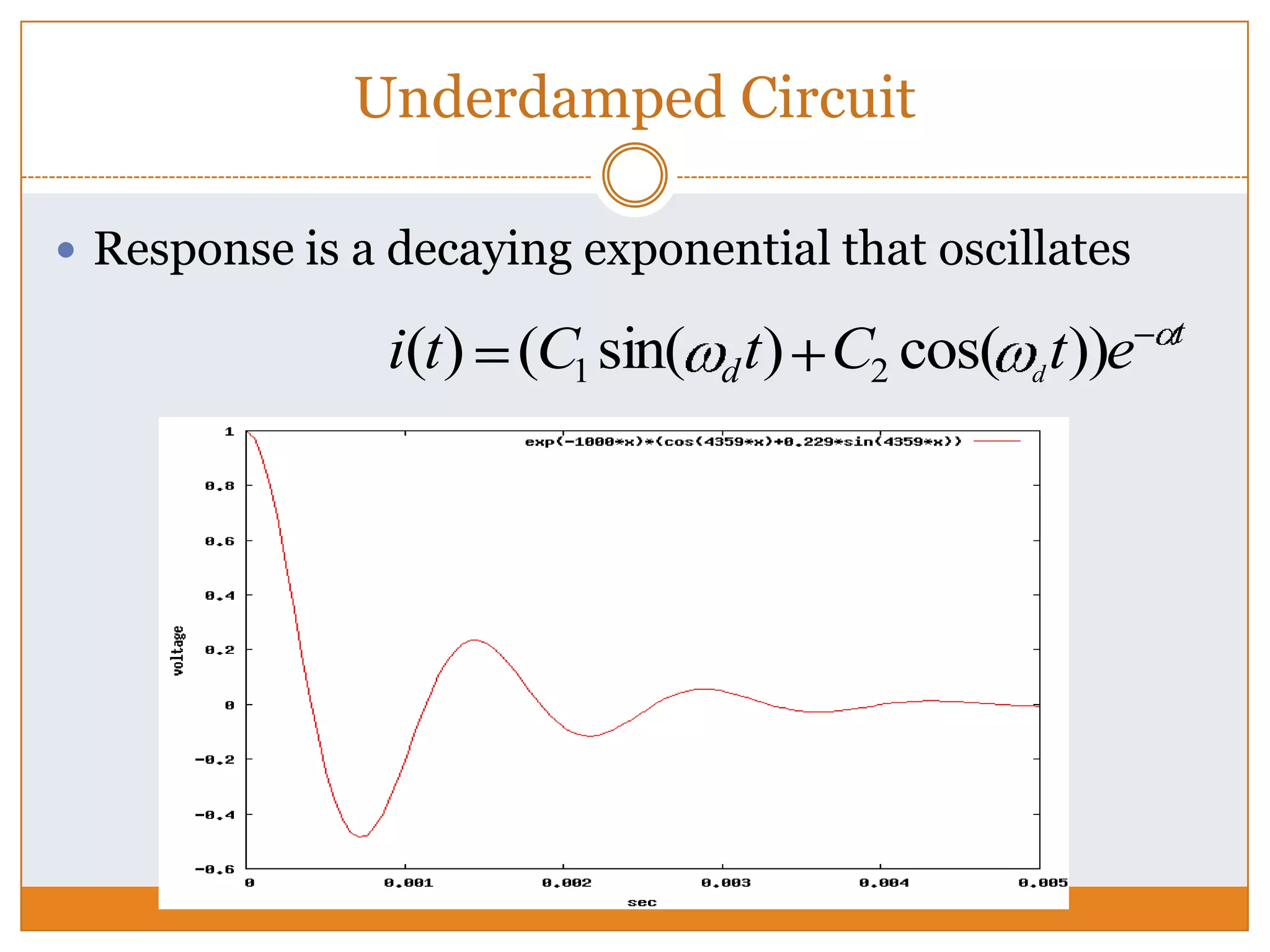
The document describes deriving a differential equation to model the behavior of an RLC circuit. It provides the component values for an RLC circuit that was designed and built. Through applying Kirchhoff's voltage law and differentiating the equation, a second order differential equation is derived. The parameters are then substituted into the equation to solve for the natural response of the underdamped circuit. The derived differential equation solution is compared to simulations and measurements from an oscilloscope.

1. MATH321
APPLIED DIFFERENTIAL
EQUATIONS
RLC Circuits and Differential
Equations

2. Designed and built RLC circuit to test response
time of current

3. Derive the constant coefficient differential
equation
 Resistance (R) = 643.108 Ω
 Inductor (L) = 9.74 × 10^-3 H
 Capacitor (C) = 9.42 × 10^-8 F

4. Kirchhoff’s Voltage Law (KVL)
The sum of voltage
drops across the
elements of a
series circuit is
equal to applied
voltage.

5. Voltage Drop per Circuit Elements
Inductor Resistor Capacitor

6. Substitute and Differentiation
Differentiate both sides for equation for
current
Substitute dQ/dt for I in original equation and
arrive at second order differential equation
Current is the rate of change of charge (in
Coulombs) with respect to time
Substitute voltage drops into equation
KVL )(tVVVV CLR
)(
1
tVQ
C
RI
dt
dI
L
)(tI
dt
dQ
)(
1
'" tVQ
C
RQLQ
)('
1
'" tVI
C
RILI

7. General forms of equation
Which is the same as:
Divide by L:
0)(
1)()(
2
2
ti
LCdt
tdi
L
R
dt
tid
0)(
)(
2
)( 2
02
2
ti
dt
tdi
dt
tid

8. Calculate Parameters for Substitution
0
1
''' I
LC
I
L
R
I
5.660272
L
R
92
0 100899.1
1
LC
0100899.1'5.66027'' 9
III
0100899.15.66027 92
RR
0)(
1)()(
2
2
ti
LCdt
tdi
L
R
dt
tid

9. Solve Characteristic Equation for R
62.32
76.33013
62.3276.33013
)1(2
)100899.1)(1(45.66027
5.66027
2
4
0)100899.1(5.66027
92
2
92
iR
iR
R
a
acb
bR
RR

10. Select Natural Response of Circuit
Three forms:
 Over-damped: Two negative real roots
 Under-damped: Two distinct complex roots
 Critically-damped: Two real, distinct roots

11. Underdamped Circuit
 Response is a decaying exponential that oscillates
t
d etCtCti d
))cos()sin(()( 21

12. Substitute Parameters into Underdamped
Equation
t
t
d
etCtCti
L
CR
etCtCti
d
d
62.32
21
2
0
22
0
0
0
21
))57.23cos()57.23sin(()(
57.231
30339999997452.0
2
62.32
76.33013
))cos()sin(()(

13. LTSpice vs Oscilloscope
t
etCtCti 62.32
21 ))57.23cos()57.23sin(()(