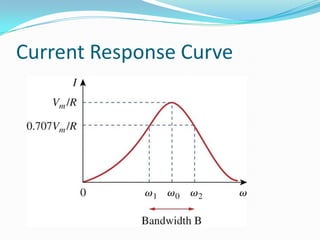
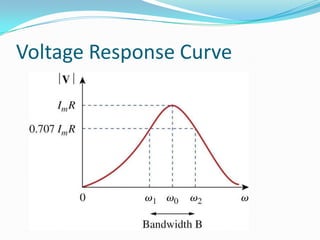
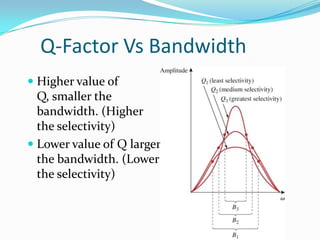
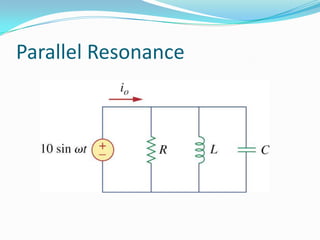
This document discusses resonance in series and parallel RLC circuits. It defines key parameters for both circuit types including resonance frequency, half-power frequencies, bandwidth, and quality factor. The series resonance circuit is analyzed showing that impedance is purely resistive at resonance, with maximum current and unity power factor. Parallel resonance is also examined, with admittance being purely conductance at resonance. Formulas for calculating important resonant characteristics are provided.

1. MECHANICAL DEPARTMENT
Elements of Electrical Engineering
ACTIVE LEARNING ASSIGNMENT
Topic: Resonance in series and parallel circuits
Guided by: Prof. Rahish

2. Group Members
 Hardik Panchal (130120119115)
 Vivek Panchal (130120119122)
 Parth Panchal (130120119120)

3. Content
 Series Resonance
 Parallel Resonance
 Important Parameters
 Resonance Frequency, o
 Half-power frequencies, 1 and 2
 Bandwidth, 
 Quality Factor, Q
 Application

4. Introduction
 Resonance is a condition in an RLC circuit in which
the capacitive and reactive reactance are equal in
magnitude, thereby resulting in a purely resistive
impedance.
 Resonance circuits are useful for constructing
filters and used in many application.

5. Series Resonance Circuit

6. At Resonance
 At resonance, the impedance consists only resistive
component R.
 The value of current will be maximum since the total
impedance is minimum.
 The voltage and current are in phase.
 Maximum power occurs at resonance since the power
factor is unity.

7. Series Resonance
CLTotal jX-jXRZ 
R
V
Z
V
I m
Total
s
m 
Total impedance of series RLC Circuit is
At resonance
The impedance now reduce to
CL XX 
RZTotal 
)X-j(XRZ CLTotal 
The current at resonance

8. Resonance Frequency
Resonance frequency is the frequency where the
condition of resonance occur.
Also known as center frequency.
Resonance frequency
rad/s
LC
1
ωo 
Hz
LC2
1

of

9. Half-power Frequency
rad/s
LC
1
2L
R
2L
R
ω
2
2 











rad/s
LC
1
2L
R
2L
R
ω
2
1 














Half-power frequencies is the frequency when the
magnitude of the output voltage or current is decrease
by the factor of 1 / 2 from its maximum value.
Also known as cutoff frequencies.

10. Bandwidth, 
rad/s)( 12 cc ωωβ 
rad/s
L
R
β 
Bandwidth,  is define as the difference between the
two half power frequencies.
The width of the response curve is determine by the
bandwidth.

11. Current Response Curve

12. Voltage Response Curve

13. Quality Factor (Q-Factor)
The ratio of resonance frequency to the bandwidth
The “sharpness” of response curve could be measured
by the quality factor, Q.
R
L
Q oo 




14. Q-Factor Vs Bandwidth
 Higher value of
Q, smaller the
bandwidth. (Higher
the selectivity)
 Lower value of Q larger
the bandwidth. (Lower
the selectivity)

15. Parallel Resonance

16. Parallel Resonance
The total admittance
ωL
ωC
1

Resonance occur when
)ωω L1/Cj(
R
1
YTotal 
321Total YYYY 
C)(-j/
1
L)(j
1
R
1
YTotal


Cj
ωL
j-
R
1
YTotal ω

17. At Resonance
 At resonance, the impedance consists only
conductance G.
 The value of current will be minimum since the
total admittance is minimum.
 The voltage and current are in phase.

18. Parameters in Parallel Circuit
rad/s
LC
1
2RC
1
2RC
1
ω
2
1 














Parallel resonant circuit has same parameters as the
series resonant circuit.
rad/s
LC
1
ωo 
rad/s
LC
1
2RC
1
2RC
1
ω
2
2 












Resonance frequency
Half-power frequencies

19. Parameters in Parallel Circuit
RC
β
ω
Q o
o

RC
1
12  ωωβ
Bandwidth
Quality Factor