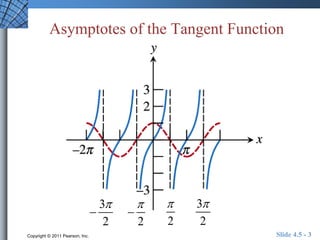
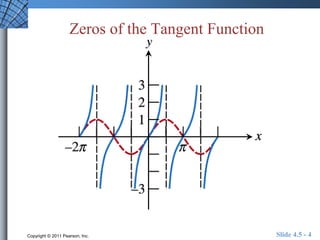
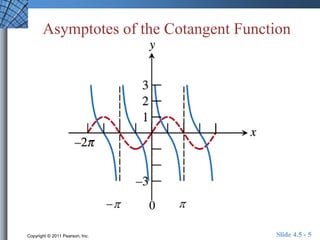
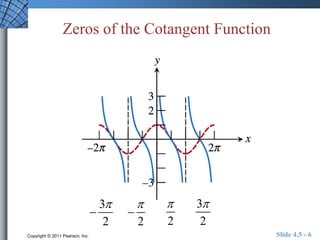
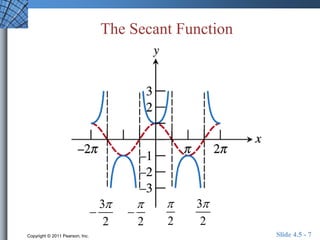
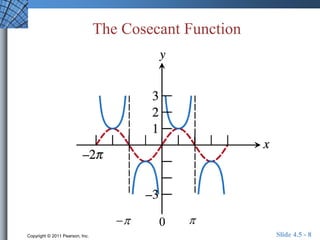
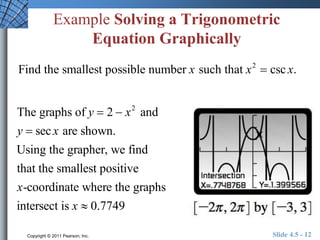
This document discusses graphs of tangent, cotangent, secant, and cosecant functions. It provides information on asymptotes and zeros of these functions. An example problem demonstrates solving a trigonometric equation graphically by finding the intersection of the graphs of y = csc(x) and y = x^2. A quick review section tests understanding of period, zeros, and asymptotes of various trigonometric functions.

1. 4.5
Graphs of
Tangent,
Cotangent,
Secant, and
Cosecant
Copyright © 2011 Pearson, Inc.

2. What you’ll learn about
 The Tangent Function
 The Cotangent Function
 The Secant Function
 The Cosecant Function
… and why
This will give us functions for the remaining
trigonometric ratios.
Copyright © 2011 Pearson, Inc. Slide 4.5 - 2

3. Asymptotes of the Tangent Function

2
3
2

3
2


2
Copyright © 2011 Pearson, Inc. Slide 4.5 - 3

4. Zeros of the Tangent Function
Copyright © 2011 Pearson, Inc. Slide 4.5 - 4

5. Asymptotes of the Cotangent Function
  0
Copyright © 2011 Pearson, Inc. Slide 4.5 - 5

6. Zeros of the Cotangent Function

2
3
2

3
2


2
Copyright © 2011 Pearson, Inc. Slide 4.5 - 6

7. The Secant Function

2
3
2

3
2


2
Copyright © 2011 Pearson, Inc. Slide 4.5 - 7

8. The Cosecant Function
 0 
Copyright © 2011 Pearson, Inc. Slide 4.5 - 8

9. Basic Trigonometry Functions
Copyright © 2011 Pearson, Inc. Slide 4.5 - 9

10. Basic Trigonometry Functions
Copyright © 2011 Pearson, Inc. Slide 4.5 - 10

11. Example Solving a Trigonometric
Equation Graphically
Find the smallest possible number x such that x2  csc x.
Copyright © 2011 Pearson, Inc. Slide 4.5 - 11

12. Example Solving a Trigonometric
Equation Graphically
Find the smallest possible number x such that x2  csc x.
The graphs of y  2  x2 and
y  sec x are shown.
Using the grapher, we find
that the smallest positive
x-coordinate where the graphs
intersect is x  0.7749
Copyright © 2011 Pearson, Inc. Slide 4.5 - 12

13. Quick Review
State the period of the function.
1. y  cos 4x
2. y  sin
1
4
x
Find the zeros and the vertical asymptotes of the function.
3. y 
x 1
x 1
4. y 
x 1
x  2x  3
5. Tell whether y  x2  4 is odd, even, or neither.
Copyright © 2011 Pearson, Inc. Slide 4.5 - 13

14. Quick Review Solutions
State the period of the function.
1. y  cos 4x  /2
2. y  sin
1
4
x 8
Find the zeros and the vertical asymptotes of the function.
3. y 
x 1
x 1
1; x  1
4. y 
x 1
x  2x  3
1; x  3, x  2
5. Tell whether y  x2  4 is odd, even, or neither. even
Copyright © 2011 Pearson, Inc. Slide 4.5 - 14