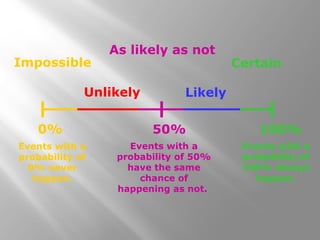
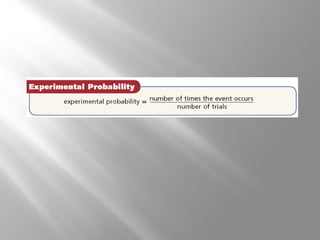
This document provides an overview of experimental probability: - It defines key terms like experiment, trial, outcome, and sample space. - It explains how to calculate experimental probability by taking the number of times an event occurs over the total number of trials. - It discusses how experimental probability can be used to make predictions about future experiments based on past results.

1. Holt Algebra 1
UNIT 11.2 EXPERIMENTALUNIT 11.2 EXPERIMENTAL
PROBABILITYPROBABILITY

2. Warm Up: Part I
Write the equivalent percent.
1. 2.
3. 4.
Write the equivalent fraction.
25%30%
16%
5.
7.
6.
8.
50% 10%
40% 35%
20%

3. Warm Up: Part II
Write the equivalent decimal.
9. 18% 10. 50%
11. 12.
0.50.18
0.90.2

4. Determine the experimental
probability of an event.
Use experimental probability to make
predictions.
Objectives

5. experiment experimental probability
trial prediction
outcome
sample space
event
probability
Vocabulary

6. An experiment is an activity involving chance.
Each repetition or observation of an experiment is a
trial, and each possible result is an outcome. The
sample space of an experiment is the set of all
possible outcomes.

7. Example 1: Identifying Sample Spaces and Outcomes
Identify the sample space and the outcome
shown for each experiment.
A. Rolling a number cube
Sample space:{1, 2, 3, 4, 5, 6}
Outcome shown: 4
B. Spinning a spinner
Sample space:{red, green,
orange, purple}
Outcome shown: green

8. Check It Out! Example 1
Identify the sample space and the outcome
shown for the experiment: rolling a number
cube.
Sample space: {1, 2, 3, 4, 5, 6}
Outcome shown: 3

9. An event is an outcome or set of outcomes in an
experiment. Probability is the measure of how
likely an event is to occur. Probabilities are
written as fractions or decimals from 0 to 1, or
as percents from 0% to 100%.

10. Impossible
As likely as not
Certain
Unlikely Likely
0%
Events with a
probability of
0% never
happen.
50%
Events with a
probability of 50%
have the same
chance of
happening as not.
100%
Events with a
probability of
100% always
happen.

11. Example 2: Estimating the Likelihood of an Event
Write impossible, unlikely, as likely as not,
likely, or certain to describe each event.
A. A shoe selected from a pair of shoes fits the
right foot. as likely as not
B. Katrina correctly guesses the last digit of a
phone number. unlikely
C. Max pulls a green marble from a bag of all green
marbles. certain
D. A randomly selected month contains the letter R.
likely

12. Check It Out! Example 2
Write impossible, unlikely, as likely as not,
likely, or certain to describe the event:
Anthony rolls a number less than 7 on a
standard number cube.
The highest number on a standard number cube
is 6. Thus it is certain the number will be less
than 7.

13. You can estimate the probability of an event by
performing an experiment. The experimental
probability of an event is the ratio of the
number of times the event occurs to the number
of trials. The more trials performed, the more
accurate the estimate will be.

15. Example 3A: Finding Experimental Probability
Outcome Frequency
Green 15
Orange 10
Purple 8
Pink 7
An experiment consists of
spinning a spinner. Use the
results in the table to find
the experimental
probability of the event.
Spinner lands on orange

16. Example 3B: Finding Experimental Probability
Outcome Frequency
Green 15
Orange 10
Purple 8
Pink 7
An experiment consists of
spinning a spinner. Use the
results in the table to find
the experimental
probability of the event.
Spinner does not land on green

17. Check It Out! Example 3a
An experiment consists of
spinning a spinner. Use the
results in the table to find
the experimental
probability of each event.
Spinner lands on red
Outcome Frequency
Red 7
Blue 8
Green 5

18. Check It Out! Example 3b
Spinner does not land on red
An experiment consists of
spinning a spinner. Use the
results in the table to find
the experimental
probability of each event.
Outcome Frequency
Red 7
Blue 8
Green 5

19. You can use experimental probability to make
predictions. A prediction is an estimate or
guess about something that has not yet
happened.

20. Example 4A: Quality Control Application
A manufacturer inspects 500 strollers and finds
that 498 have no defects.
What is the experimental probability that a
stroller chosen at random has no defects?
Find the experimental probability that a stroller has
no defects.
= 99.6%
The experimental probability that a stroller has no
defects is 99.6%.

21. Example 4B: Manufacturing Application
A manufacturer inspects 500 strollers and finds
that 498 have no defects.
The manufacturer shipped 3500 strollers to a
distribution center. Predict the number of
strollers that are likely to have no defects.
Find 99.6% of 3500.
0.996(3500) = 3486
The prediction is that 3486 strollers will have no
defects.

22. Check It Out! Example 4a
A manufacturer inspects 1500 electric
toothbrush motors and finds 1497 have no
defects.
What is the experimental probability that a
motor chosen at random will have no defects?
Find the experimental probability that a motor has
no defects.
= 99.8%

23. Check It Out! Example 4b
A manufacturer inspects 1500 electric
toothbrush motors and finds 1497 have no
defects.
There are 35,000 motors in a warehouse.
Predict the number of motors that are likely to
have no defects.
Find 99.8% of 35,000.
0.998(35000) = 34930
The prediction is that 34,930 motors will have no
defects.

24. 1. Identify the sample space and the outcome
shown for selecting a marble.
Lesson Quiz: Part I
Sample space: {red, green, yellow}
Outcome shown: red

25. Lesson Quiz: Part II
2. An experiment consists of spinning a spinner.
Use the results in the table to find the
experimental probability of landing on blue.
Outcome Frequency
Red 9
Blue 6
Yellow 5

26. Lesson Quiz: Part III
3. The neighbors’ dog barked at Tana the last 4
out of 5 times she walked by their house.
a. What is the experimental probability that
the dog barks at Tana when she walks past
the house? 80%
b. Predict the number of times the dog will bark
at Tana if she walks past the house 45 times.
36

27. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.