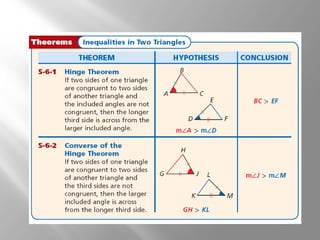
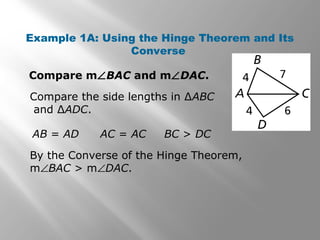
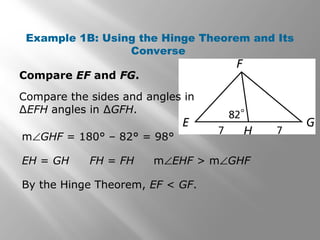
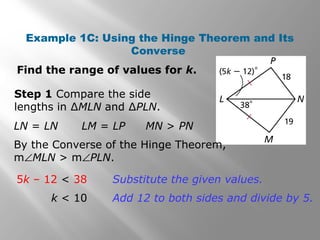
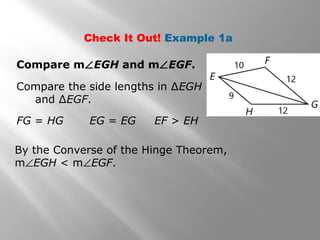
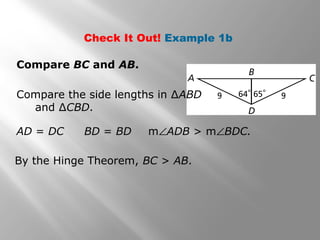
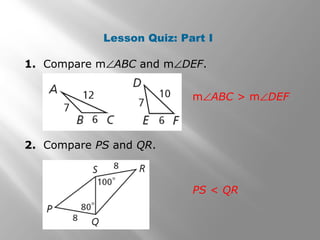
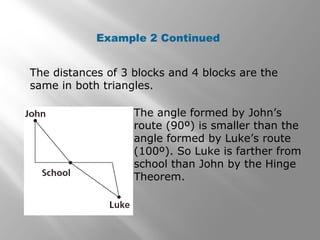
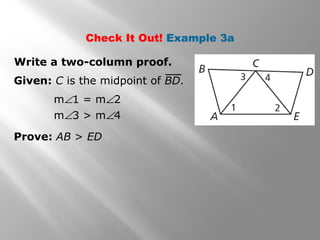
1) The document discusses using inequalities to compare angles and side lengths in two triangles. It provides examples of applying the hinge theorem and its converse to determine relationships between angles and sides. 2) One example involves comparing the distances traveled by two people leaving school at different routes to determine who is farther from school. 3) The document also demonstrates how to write two-column proofs to prove triangle relationships based on given information about the triangles. It includes practice problems for the reader to check their understanding.

1. UNIT 5.7 INEQUALITIESUNIT 5.7 INEQUALITIES
IN TWO TRIANGLESIN TWO TRIANGLES

2. Warm Up
1. Write the angles in order from smallest to
largest.
2. The lengths of two sides of a triangle are 12 cm
and 9 cm. Find the range of possible lengths for
the third side.
∠X, ∠Z, ∠Y
3 cm < s < 21 cm

3. Apply inequalities in two triangles.
Objective

5. Example 1A: Using the Hinge Theorem and Its
Converse
Compare m∠BAC and m∠DAC.
Compare the side lengths in ∆ABC
and ∆ADC.
By the Converse of the Hinge Theorem,
m∠BAC > m∠DAC.
AB = AD AC = AC BC > DC

6. Example 1B: Using the Hinge Theorem and Its
Converse
Compare EF and FG.
By the Hinge Theorem, EF < GF.
Compare the sides and angles in
∆EFH angles in ∆GFH.
EH = GH FH = FH m∠EHF > m∠GHF
m∠GHF = 180° – 82° = 98°

7. Example 1C: Using the Hinge Theorem and Its
Converse
Find the range of values for k.
Step 1 Compare the side
lengths in ∆MLN and ∆PLN.
By the Converse of the Hinge Theorem,
m∠MLN > m∠PLN.
LN = LN LM = LP MN > PN
5k – 12 < 38
k < 10
Substitute the given values.
Add 12 to both sides and divide by 5.

8. Example 1C Continued
Step 2 Since ∠PLN is in a triangle, m∠PLN > 0°.
Step 3 Combine the two inequalities.
The range of values for k is 2.4 < k < 10.
5k – 12 > 0
k < 2.4
Substitute the given values.
Add 12 to both sides and divide by 5.

9. Check It Out! Example 1a
Compare m∠EGH and m∠EGF.
Compare the side lengths in ∆EGH
and ∆EGF.
FG = HG EG = EG EF > EH
By the Converse of the Hinge Theorem,
m∠EGH < m∠EGF.

10. Check It Out! Example 1b
Compare BC and AB.
Compare the side lengths in ∆ABD
and ∆CBD.
By the Hinge Theorem, BC > AB.
AD = DC BD = BD m∠ADB > m∠BDC.

11. Example 2: Travel Application
John and Luke leave school at the same time.
John rides his bike 3 blocks west and then 4
blocks north. Luke rides 4 blocks east and then
3 blocks at a bearing of N 10º E. Who is farther
from school? Explain.

12. Example 2 Continued
The distances of 3 blocks and 4 blocks are the
same in both triangles.
The angle formed by John’s
route (90º) is smaller than the
angle formed by Luke’s route
(100º). So Luke is farther from
school than John by the Hinge
Theorem.

13. Check It Out! Example 2
When the swing ride is at full speed, the chairs
are farthest from the base of the swing tower.
What can you conclude about the angles of the
swings at full speed versus low speed? Explain.
The ∠ of the swing at full
speed is greater than the
∠ at low speed because
the length of the triangle
on the opposite side is the
greatest at full swing.

14. Example 3: Proving Triangle Relationships
Write a two-column proof.
Given:
Prove: AB > CB
Proof:
Statements Reasons
1. Given
2. Reflex. Prop. of ≅
3. Hinge Thm.

15. Check It Out! Example 3a
Write a two-column proof.
Given: C is the midpoint of BD.
Prove: AB > ED
m∠1 = m∠2
m∠3 > m∠4

16. 1. Given
2. Def. of Midpoint
3. Def. of ≅ ∠s
4. Conv. of Isoc. ∆ Thm.
5. Hinge Thm.
1. C is the mdpt. of BD
m∠3 > m∠4,
m∠1 = m∠2
3. ∠1 ≅ ∠2
5. AB > ED
Statements Reasons
Proof:

17. Write a two-column proof.
Given:
Prove: m∠TSU > m∠RSU
Statements Reasons
1. Given
3. Reflex. Prop. of ≅
4. Conv. of Hinge Thm.
2. Conv. of Isoc. Δ Thm.
1. ∠SRT ≅ ∠STR
TU > RU
∠SRT ≅ ∠STR
TU > RU
Check It Out! Example 3b
4. m∠TSU > m∠RSU

18. Lesson Quiz: Part I
1. Compare m∠ABC and m∠DEF.
2. Compare PS and QR.
m∠ABC > m∠DEF
PS < QR

19. Lesson Quiz: Part II
3. Find the range of values for z.
–3 < z < 7

20. Statements Reasons
1. Given
2. Reflex. Prop. of ≅
3. Conv. of Hinge Thm.3. m∠XYW < m∠ZWY
Given:
Prove: m∠XYW < m∠ZWY
4. Write a two-column proof.
Lesson Quiz: Part III
Proof:

21. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.