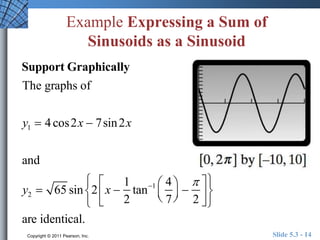
This document discusses trigonometric identities for sums and differences of angles. It provides examples of using identities for cosine, sine, and tangent of sums and differences to find exact trigonometric values without a calculator. One example expresses the sum of two sinusoids as a single sinusoid, finding the amplitude, frequency, and phase shift. In general, the identities allow decomposing compound angle expressions into combinations of basic trigonometric functions of the component angles.

1. 5.3
Sum and
Difference
Identities
Copyright © 2011 Pearson, Inc.

2. What you’ll learn about
 Cosine of a Difference
 Cosine of a Sum
 Sine of a Difference or Sum
 Tangent of a Difference or Sum
 Verifying a Sinusoid Algebraically
… and why
These identities provide clear examples of how different
the algebra of functions can be from the algebra of real
numbers.
Copyright © 2011 Pearson, Inc. Slide 5.3 - 2

3. Cosine of a Sum or Difference
cosu  v cosucos v msinusin v
(Note the sign switch in either case.)
Copyright © 2011 Pearson, Inc. Slide 5.3 - 3

4. Example Using the Cosine-of-a-
Difference Identity
Find the exact value of cos 75º without using a calculator.
Copyright © 2011 Pearson, Inc. Slide 5.3 - 4

5. Example Using the Cosine-of-a-
Difference Identity
Find the exact value of cos 75º without using a calculator.
cos 75º  cos 45º 30º
 cos45º cos30º  sin 45º sin 30º

2
2






3
2






2
2






1
2

 

 

6  2
4
Copyright © 2011 Pearson, Inc. Slide 5.3 - 5

6. Sine of a Sum or Difference
sinu  v sinu cosv  sinv cosu
(Note that the sign does not switch in either case.)
Copyright © 2011 Pearson, Inc. Slide 5.3 - 6

7. Example Using the Sum and
Difference Formulas
Write the following expression as the sine or
cosine of an angle: sin

3
cos

4
 sin

4
cos

3
Copyright © 2011 Pearson, Inc. Slide 5.3 - 7

8. Example Using the Sum and
Difference Formulas
Write the following expression as the sine or
cosine of an angle: sin
Recognize sin

3
cos

4

3
cos
 sin

4

4
 sin
cos

3

4
cos

3
as the sin(u  v).
sin

3
cos

4
 sin

4
cos

3
 sin

3


4

 

 
 sin
7
12
Copyright © 2011 Pearson, Inc. Slide 5.3 - 8

9. Tangent of a Difference of Sum
tanu  v
sinu  v
cosu  v

sinu cosv  sinv cosu
cosu cosvmsinusinv
or
tanu  v
tanu  tanv
1mtanu tanv
Copyright © 2011 Pearson, Inc. Slide 5.3 - 9

10. Example Expressing a Sum of
Sinusoids as a Sinusoid
Find values for a, b, and h so that for all x,
4 cos2x  7sin2x  asin b x  h    .
Copyright © 2011 Pearson, Inc. Slide 5.3 - 10

11. Example Expressing a Sum of
Sinusoids as a Sinusoid
4 cos2x  7sin2x  asin b x  h   

is a sinusoid with period
2
2
  , so b  2
4 cos2x  7sin2x  asin 2 x  h   

 asin2x  2h
 asin2x cos2h  acos2x sin2h
4 cos2x  7sin2x  asin2hcos2x  acos2hsin2x,
so 4  asin2h and  7  acos2h
Copyright © 2011 Pearson, Inc. Slide 5.3 - 11

12. Example Expressing a Sum of
Sinusoids as a Sinusoid
so 4  asin2h and  7  acos2h
sin2h  
4
a
and cos2h  
7
a
so tan2h 
4 a
7 a

4
7
so possible values of 2h are tan1 4
7

 

 
 n
Copyright © 2011 Pearson, Inc. Slide 5.3 - 12

13. Example Expressing a Sum of
Sinusoids as a Sinusoid
To find a, we use sin2h  
4
a
and cos2h  
7
a
Because a is the hypotenuse,
a  72
 42
 65
Thus,


4 cos2x  7sin2x  65 sin 2 x 
1
2
tan1 4
7

 

 


2
 

 

Copyright © 2011 Pearson, Inc. Slide 5.3 - 13

14. Example Expressing a Sum of
Sinusoids as a Sinusoid
Support Graphically
The graphs of
y1  4 cos2x  7sin2x
and


y2  65 sin 2 x 
1
2
tan1 4
7

 

 


2
 

 

are identical.
Copyright © 2011 Pearson, Inc. Slide 5.3 - 14

15. Example Expressing a Sum of
Sinusoids as a Sinusoid
Interpret
The values are a  65, b  2, and h 
1
2
tan1 4
7

 

 

2
(other values are possible).
The amplitude is 65, the peridod is  , and
the phase shift is
1
2
tan1 4
7

 

 

2
radians.
Copyright © 2011 Pearson, Inc. Slide 5.3 - 15

16. Quick Review
Express the angle as a sum or difference of special angles
(multiples of 30o, 45o,  /6, or  /4). Answers are not unique.
1. 15o
2.  /12
3. 75o
Tell whether or not the identity f (x  y)  f (x)  f (y)
holds for the function f .
4. f (x)  16x
5. f (x)  2ex
Copyright © 2011 Pearson, Inc. Slide 5.3 - 16

17. Quick Review Solutions
Express the angle as a sum or difference of special angles
(multiples of 30o, 45o,  /6, or  /4). Answers are not unique.
1. 15o 45o  30o
2.  /12

3


4
3. 75o 30o  45o
Tell whether or not the identity f (x  y)  f (x)  f (y)
holds for the function f .
4. f (x)  16x yes
5. f (x)  2ex no
Copyright © 2011 Pearson, Inc. Slide 5.3 - 17