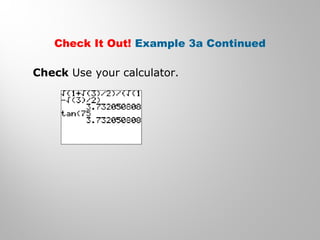
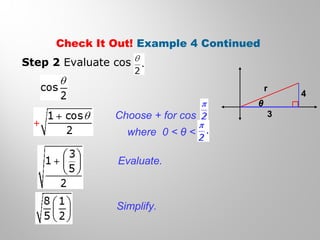
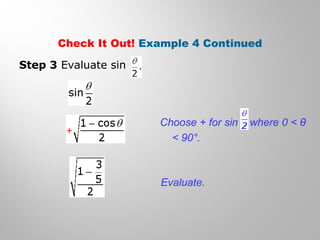
This document discusses double-angle and half-angle identities in trigonometry. It provides examples of using these identities to evaluate expressions and prove trigonometric identities. Key double-angle identities covered are sin(2θ), cos(2θ), and tan(2θ). The document also derives the half-angle identities and provides examples of using them to find exact trigonometric values.

1. UNIT 10.7 DOUBLE-ANGLE ANDUNIT 10.7 DOUBLE-ANGLE AND
HALF-ANGLE IDENTITIESHALF-ANGLE IDENTITIES

2. Warm Up
Find tan θ for 0 ≤ θ ≤ 90°, if
1.
2.
3.

3. Evaluate and simplify expressions by using double-
angle and half-angle identities.
Objective

4. You can use sum identities to derive the
double-angle identities.
sin 2θ = sin(θ + θ)
= sinθ cosθ + cosθ sinθ
= 2 sinθ cosθ

5. You can derive the double-angle identities for
cosine and tangent in the same way. There are
three forms of the identity for cos 2θ, which are
derived by using sin2
θ + cos2
θ = 1. It is common
to rewrite expressions as functions of θ only.

6. Example 1: Evaluating Expressions with Double-Angle
Identities
Find sin2θ and tan2θ if sinθ = and 0°<θ<90°.
Step 1 Find cosθ to evaluate sin2θ = 2sinθcosθ.
Method 1 Use the reference angle.
In Ql, 0° < θ < 90°, and sinθ =
x2
+ 22
= 52
θ
r = 5
y = 2
x
Use the Pythagorean
Theorem.
Solve for x.

7. Example 1 Continued
Method 2 Solve cos2
θ = 1 – sin2
θ.
cos2
θ = 1 – sin2
θ
cosθ =
Substitute for cosθ.
Simplify.

8. Example 1 Continued
Step 2 Find sin2θ.
sin2θ = 2sinθcosθ Apply the identity for sin2θ.
Simplify.
Substitute for sinθ and
for cosθ.

9. Example 1 Continued
Step 3 Find tanθ to evaluate tan2θ = .
Apply the tangent ratio identity.
Simplify.
Substitute for sinθ and
for cosθ.

10. Example 1 Continued
Step 4 Find tan 2θ.
Apply the identity for tan2θ.
Substitute for tan θ.

11. Example 1 Continued
Step 4 Continued
Simplify.

12. The signs of x and y depend on the quadrant for
angle θ.
sin cos
Ql + +
Qll + –
Qlll – –
QlV – +
Caution!

13. Find tan2θ and cos2θ if cosθ = and
270°<θ<360°.
Method 1 Use the reference angle.
Check It Out! Example 1
Step 1 Find tanθ to evaluate tan2θ = .
In QlV, 270° < θ < 360°, and cosθ =
12
+ y2
= 32
Use the Pythagorean
Theorem.
Solve for y. θ
r=3
x=1
y= –2√ 2

14. Check It Out! Example 1 Continued
Step 2 Find tan2θ.
Apply the identity for tan2θ.
Simplify.
tan2θ =
Substitute –2 for tanθ.

15. Check It Out! Example 1 Continued
Step 3 Find cos2θ.
cos2θ = 2cos2
θ – 1 Apply the identity for cos2θ.
Simplify.
Substitute for cosθ.

16. You can use double-angle identities to prove
trigonometric identities.

17. Example 2A: Proving identities with Double-Angle
Identities
Prove each identity.
sin 2θ = 2tanθ – 2tanθ sin2
θ Choose the right-hand
side to modify.
= 2tanθ (1– sin2
θ) Factor 2tanθ.
= 2tanθ cos2
θ
Rewrite using 1 –sin2
θ =
cos2
θ.
= 2(tanθcosθ)cosθ Regroup.
= 2sinθcosθ
Rewrite using tanθcosθ
= sinθ.
= sin2θ Apply the identity for
sin2θ.

18. Example 2B: Proving identities with Double-Angle
Identities
cos2θ = (2 – sec2
θ)(1 – sin2
θ)
cos2θ = (2 – sec2
θ)(1 – sin2
θ)
= (2 – sec2
θ)(cos2
θ)
= 2cos2
θ – 1
= cos2θ
Choose the right-hand side
to modify.
Rewrite using 1 – sin2
θ =
cos2
θ.
Expand and simplify.
Apply the identity for
cos2
θ.

19. Choose to modify either the left side or the right
side of an identity. Do not work on both sides at
once.
Helpful Hint

20. Check It Out! Example 2a
cos4
θ – sin4
θ = cos2θ
(cos2
θ – sin2
θ)(cos2
θ + sin2
θ) =
(1)(cos2θ) =
cos2θ = cos2θ
Factor the left side.
Rewrite using
1 = cos2
θ + sin2
θ and
cos2θ = cos2
θ – sin2
θ.
Simplify.
Prove each identity.

21. Check It Out! Example 2b
Prove each identity.
Rewrite tan θ ratio identity
and Pythagorean identity.
Reciprocal sec θ identity
and simplify fraction.

22. Check It Out! Example 2b Continued
Prove each identity.
Simplify.
Double angle identity.

23. You can use double-angle identities for cosine to derive
the half-angle identities by substituting for θ. For
example, cos2θ = 2 cos2
θ – 1 can be rewritten as cosθ = 2
cos2
– 1. Then solve for cos

24. Half-angle identities are useful in calculating exact
values for trigonometric expressions.

25. Example 3A: Evaluating Expressions with Half-Angle
Identities
Use half-angle identities to find the exact value
of cos 15°.
Positive in Ql.
Simplify.
Cos 30° =

26. Example 3A Continued
Check Use your calculator.

27. Example 3B: Evaluating Expressions with Half-Angle
Identities
Use half-angle identities to find the exact value
of .
Negative in Qll.

28. Example 3B Continued
Simplify.

29. Example 3B Continued
Check Use your calculator.

30. Check It Out! Example 3a
Use half-angle identities to find the exact value
of tan 75°.
tan (150°)
Positive in Ql.
Simplify.

31. Check It Out! Example 3a Continued
Check Use your calculator.

32. Check It Out! Example 3b
Use half-angle identities to find the exact value
of .
Negative in Qll.

33. Check It Out! Example 3b Continued
Simplify.
Check Use your calculator.

34. Example 4: Using the Pythagorean Theorem with Half-
Angle Identities
Find cos and tan if tan θ = and 0<θ<
Step 1 Find cos θ to evaluate the half-angle
identities. Use the reference angle.
In Ql, 0 < θ < and tanθ =
242
+ 72
= x2
Thus, cosθ =
Pythagorean Theorem.
Solve for the missing
side x.

35. Example 4 Continued
x
7
24
θ
Step 2 Evaluate cos
Evaluate.
Choose + for cos
where 0 < θ <

36. Simplify.
Example 4 Continued

37. Example 4 Continued
Step 3 Evaluate tan
Choose + for tan where
0 < θ <
Evaluate.

38. Example 4 Continued
Simplify.

39. Check It Out! Example 4
Step 1 Find cos θ to evaluate the half-angle
identities. Use the reference angle.
42
+ 32
= r 2 Pythagorean Theorem.
Solve for the missing
side r.
Find sin and cos if tan θ = and 0 < θ < 90.
In Ql, 0 < θ < and tanθ =
r =
Thus, cosθ = .

40. Check It Out! Example 4 Continued
r
4
3
θ
Step 2 Evaluate cos
Evaluate.
Choose + for cos
where 0 < θ <
Simplify.

41. Check It Out! Example 4 Continued

42. Check It Out! Example 4 Continued
Step 3 Evaluate sin
Choose + for sin where 0 < θ
< 90°.
Evaluate.

43. Check It Out! Example 4 Continued
Simplify.

44. Lesson Quiz: Part I
1. Find cos and cos 2θ if sin θ = and 0 < θ <
2. Prove the following identity:

45. Lesson Quiz: Part II
3. Find the exact value of cos 22.5°.

46. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.