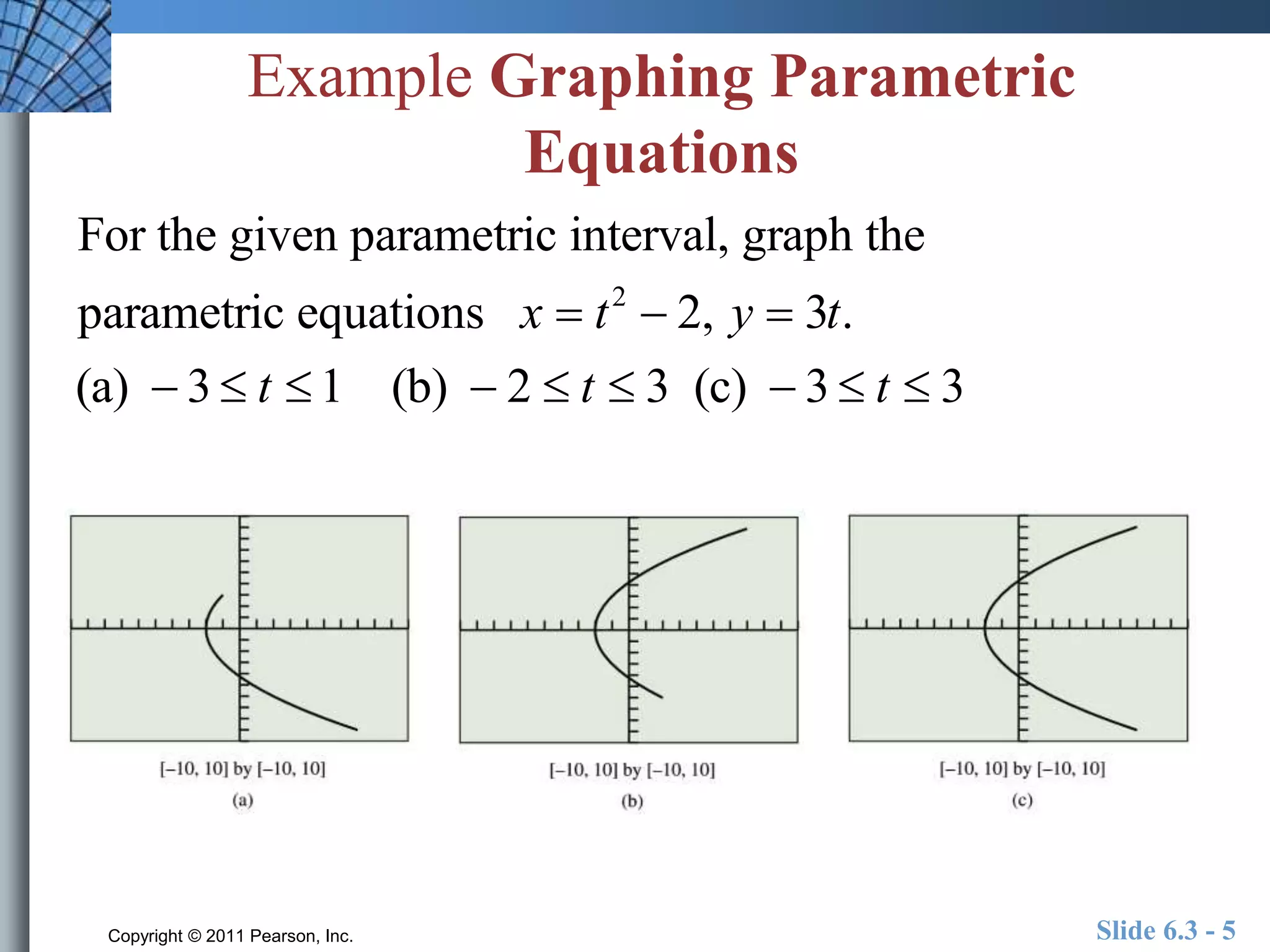
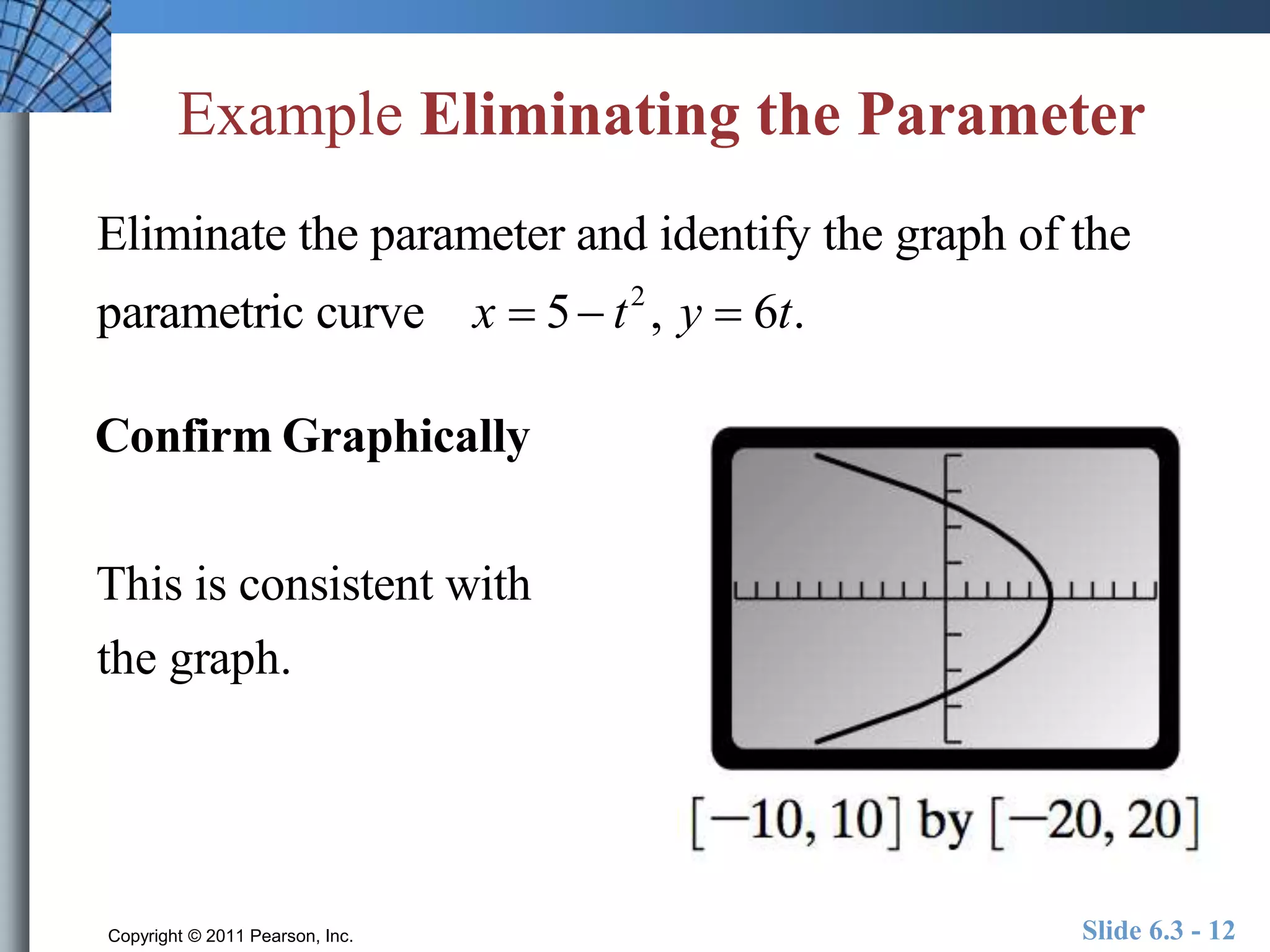
This document discusses parametric equations and motion. It defines parametric curves as graphs of ordered pairs (x,y) where x and y are functions of a parameter t. Parametric equations can be used to model the path of objects in motion. Examples are provided of graphing parametric equations, eliminating the parameter to get a standard equation, and finding parametric equations to represent a line. The document also contains sample problems testing understanding of parametric equations and related concepts.