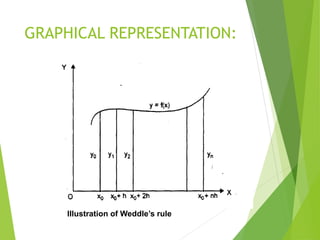
The document describes Weddle's rule, a numerical integration method. It provides background on Thomas Weddle, who introduced the rule. Weddle's rule approximates integrals using a 6th degree Newton-Cotes formula. The document explains the formula for Weddle's rule, provides an example calculation, and discusses applications for numerical integration such as calculating power and energy over time.

2. Presentation topic
Weddle’s rule

3. Course title
Numerical Analysis -II:
Course code: Math-402
Presented To: Ma’am Samra
Presented By: Group-5

5. Team work
 Data searched by:
Rida Munir,Asma Jamil And Farwa
 Data composed by:
Asma Jamil and Farwa Saba
 Data presented by:
Rida Munir
 Query satisfation will be done by:
Rida Munir
 Data will be explained by:
Asma Jamil,Farwa Saba,Rida Munir, Maria Nawaz
Iqrq Mushtaq & Fakhra Mubeen

6. HISTORY:
 Thomas Weddle (1817 November 30
Stamfordham, Northumberland–1853 December
4 Bagshot) was a mathematician who introduced
the Weddle surface. He was mathematics
professor at the Royal Military College at
Sandhurst.
 Weddle's Rule is a method of integration, the
Newton-Cotes formula with N=6

7. INTRODUCTION:
 Numerical integration is the process of computing the
value of definite integral from a set of numerical values of
the integrand. The process is sometimes referred as
mechanical quadrature. The approximate values of the
definite integral which are either impossible to be
computed analytically or for which anti derivative is too
complex to be used.
 The inverse process to differentiation in calculus is
represented by
I =∫f (x)dx

8. Weedle’s rule :
 Let the values of a function f(x) be tabulated at points xi
equally spaced by h= xi+1- xi so the f1=f(x1),f2=f(x2),… .
Then Weddle’s rule approximating the integral of f(x) is
given by putting n = 6 in the Newton Cote’s formula. For
Weddle’s rule the number of subinterval should be taken
as multiple of 6.
 Since we take n = 6 means f(x) can be approximated by a
polynomial of 6th degree so that seventh and higher order
differences are vanishes in the Newton Cote’s formula.

9. GRAPHICAL REPRESENTATION:
Illustration of Weddle’s rule

10. FORMULA:
 .ff5ff6ff5f
10
h3
dxf(x)I 6543210
b
a

6
ab
h

Where n = 6,

11. DERIVATION:
 To find the area we consider the integral as follows
I=∫f(x)dx=∫f(x)dx=∫f(x)dx
Where xi =a+ih and h=b-a/6
Substituting n=6 in the above equation,we get
I=6h[f(a)+3∆f(a)+9/2∆^2f(a)+4∆^3f(a)+1/24×246/5∆^4f(a)+1/120×66
∆^5f(a)+1/720×246/7∆^6f(a)]
I =6h/20 [ 20 f(a) + 60 {f(a+h)-f(a)} + 90 {f(a+2h)-2f(a+h)+f(a)} +
80 {f(a+3h)-3f(a+2h)+3f(a+h)-f(a)}
+ 41 { f(a+4h)-4f(a+3h)+6 f(a+2h) -4f(a+h)+f(a)} + 11 { f(a+5h)-5
f(a+4h) +10 f(a+3h) -10 f(a+2h)+ 5 f(a+h) – f(a) } + { f( a+6h) -
6f(a+5h) +15 f(a+4h)- 20 f(a+3h) +15 f(a+2h) – 6 f(a+h) + f(a) } ]
After simplifying we get Weddle’s rule as follows
I = 8h/10[ f(a) +5 f(a+h) + f(a+2h) + 6 f(a+3h) + f(a+4h) +5
f(a+5h) + f(a+6h) ]

12. Evaluate
.xdx2sineI
0.5
0.2
x
 Using Weddl’s rule
05.0
6
0.20.5
6
ab
h 




Calculate the values of x2sinef(x) x

x 0.2 0.25 0.3 0.35 0.4 0.45 0.5
f(x) 0.475 0.165 0.716 0.914 1.070 1.228 1.387
 .ff5ff6ff5f
10
h3
dxf(x)I 6543210
b
a
 
  .2760.03873.1)2285.1(50702.1)9142.0(67622.0)6156.0(54756.0
10
)05.03(
I 

13. APPLICATIONS
 1.Weddle’s rule is very used when have to solve multiple
integrals.
 2.It gives more accurate solution as compare to any other
formulas of Quadrature rule.
 3.Weddle’s rule is very useful whenever you have a definite
integral that can not be evaluated in closed form,or that is
very difficult to evaluate in closed form. Since most “real
world” integrals fall into one of these two categories.
 4.weddles rule is one of the most useful integration
techniques,especially when you have a working knowledge
of programming language like C or MATLAB.

14. APPLICATION:
 5. One application relates to power and energy. Power is the
rate of change of energy. (Some people prefer to think of it
as the "flow" of energy.) It can be written as
P = dE/dt
If you multiply both sides of this equation by dt, you have
(dt)P = dE
dE = Pdt

15. APPLICATIONS:
 Integrating both sides of the equation gives you
∫dE = ∫(P)dt
E = ∫(P)dt
Imagine you have
P = ((sint)^2 e^-t )/ln(t) Watts

16. SUGESTIONS:
 How would you integrate something
like this?
 How would you integrate something
like this? Well... chances are, you
would need to use a computer. How
does the computer solve it? It uses a
numerical technique such as
Weddle's rule.

17. REFERENCES:
 John.L.Gidley, Howard F. Rase (1955): Numerical
integration:A tool for chemical engineers, J.
Chem. Educ. , 32(10),535.
 Golub G.H., Welsch J. H. (1969): Calculation of
Gaussian quadrature rules,Mathematics of
computation,23, 221-230.
 Lessels, Jonathan D (1982): Numerical
calculation of Mean mission duration, Reliability
IEEE transaction Vol R- 31, Issue 5, 420-422