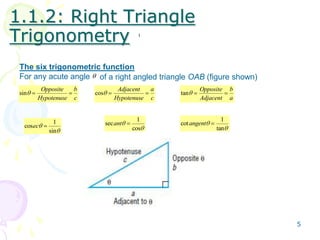
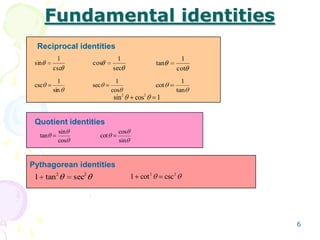
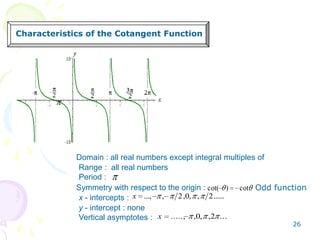
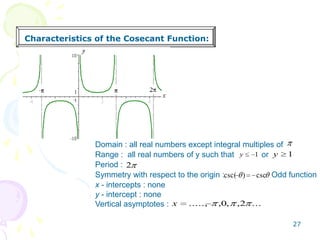
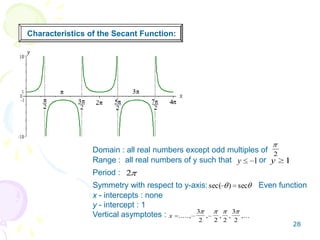
This document provides an overview of trigonometric functions. It covers angles and their measurement in degrees and radians. It then discusses right triangle trigonometry, defining the six trigonometric functions and properties like fundamental identities. Special angle values are computed for 30, 45, and 60 degrees. Trig functions of general angles and the unit circle approach are introduced. Graphs of sine, cosine, tangent, cotangent, cosecant and secant functions are examined.

1. TOPIC 1.1 -
TRIGONOMETRIC
FUNCTIONS
1.1.1: Angles and Their Measure
1.1.2: Right Triangle Trigonometry
1.1.3: Computing the Values of Trigonometric Functions of
Acute Angles
1.1.4: Trigonometric Functions of General Angles
1.1.5: Unit Circle Approach; Properties of the Trigonometric
Functions
1.1.6: Graphs of the Sine and Cosine Functions
1.1.7: Graphs of the Tangent, Cotangent, Cosecant, and
Secant Functions
1

2. 1.1.1: Angles and their
measure
Angles:
An angle is formed by initial side and terminal side
The common point for this 2 sides is the vertex of the angle
An angle is in standard position if:
i) Its vertex is at the origin of a rectangle coordinate system
ii) Its initial side lies along the positive x-axis
Positive angles generated by counterclockwise rotation
Negative angles generated by clockwise rotation
An angle is called a quadrantal angle if its terminal side lies
on the x-axis or the y-axis
2

3. Measuring angles using degrees
360
90
1 60
1 60
• One complete revolution =
• One quarter of a complete revolution =
• One degree equals 60 minutes, i.e.
• One minute equals 60 seconds, i.e.
.
= one right angle
Angles classified by their degree measurement:
a.Acute b. right c.Obtuse d.Straight
angle angle angle angle
3

4. 2
Measuring angles using radians
•One complete revolution = radians
• One radian is the angle subtended at the center of a circle by an arc of the
circle equal in length to the radius of the circle.
c
180
1
1
180c

radians
4
radians
3
4
Example:
Convert each angle in degrees to radians
a. 60 b. 270 c. -300
Convert each angle in radians to degrees
a. b. c. 6 radians
4

5. 1.1.2: Right Triangle
Trigonometry
The six trigonometric function
For any acute angle of a right angled triangle OAB (figure shown)
sin
Opposite
Hypotenuse
b
c
cos
Adjacent
Hypotenuse
a
c
tan
Opposite
Adjacent
b
a
cos
sin
ec
1 sec
cos
ant
1
cot
tan
angent
1
5

6. Fundamental identities
csc
1
sin
sec
1
cos
cot
1
tan
sin
1
csc sec
cos
1
cot
tan
1
Reciprocal identities
tan
sin
cos
cot
cos
sin
Quotient identities
sin cos2 2
1
22
sectan1 1 2 2
cot csc
Pythagorean identities
6

7. Trigonometric functions
and complements
)90cos(sin 
)90sin(cos 
)90cot(tan 
)90tan(cot 
)90csc(sec 
)90sec(csc 
Cofunction identities
The value of a trigonometric function of
of the complement of
is equal to the cofunction

46sin
12
cot
Example:
Find a cofunction with the same value as the given expression
a) b)
7

8. Solving Right Triangles
180
90
To solve a right triangle means to find the missing lengths of its sides and
the measurements of its angles.
Some general guidelines for solving right triangles:
1. Need to know an angle and a side, or else two sides.
2. Then, make use of the Pythagorean Theorem and the fact that
the sum of the angles of a triangle is
in a right triangle is
.
, and the sum of the unknown angles
c
a
b
A
222
bac 222
bac
c2=a2+b2 A+B=90
8

9. Example:
If b = 2 and , find a, c, and .
Solution :
40
2
c
a
40
9

10. 1.1.3: COMPUTING THE VALUES OF
TRIGONOMETRIC FUNCTIONS OF ACUTE
ANGLE
30 
60 
45
We use isosceles triangle and equilateral triangle to find these special angles of
, and
sin60
3
2

cos60
1
2

tan60 3
sin30
1
2

cos30
3
2

tan30
1
3

sin45
1
2
2
2

cos45
1
2

tan45 1
10

11. 1.1.4: TRIGONOMETRIC FUNCTIONS OF
GENERAL ANGLES
1st Quadrant2nd
Quadrant
3rd Quadrant 4th Quadrant
Definitions of trigonometric functions of any angle
22
yxr
Let be any angle in standard position, and let P = (x,y) be a point on
. If
is the distance from (0,0) to (x,y), then the 6 trigonometric functions of
are defined by the following ratios:
the terminal side of
r
y
sin r
x
cos 0,tan x
x
y
0,csc y
y
r
0,sec x
x
r
0,cot y
y
x
x
r
y
x
11

12. Example:
1.Let P = (4, -3) be a point on the terminal side of
six trigonometric functions of
2. Evaluate, if possible the cosine function and the cosecant function at
. Find each of the
the following 4 quadrantal angles
2
2
3
a)
= 180º
=
d) =
b)= 0
c)
**Quadrantal Angles: 0 ,90 ,180 ,270 ,360
12

13. The signs of the trigonometric function
x
y
All (sin , cos, tan)sine
cosinetangent
If
depends on the quadrant in which lies
is not a quadrantal angle, the sign of a trigonometric function
Example:
Given tan = -1/3 and cos < 0, find sin and sec
13

14. 2. The trigonometric functions of coterminal angles are equal.
Example:
Coterminal Angles
Two angles in standard position are said to be coterminal if they have
the same terminal side.
Example:
For example, the angles 60 and 420 are coterminal, as are the angles -40
and 320 .
Note:
k2
)2sin(sin k
1. is coterminal with , k is any integer.
14

15. Definition of a reference angle
Let
Its reference angle is the positive acute angle formed by the terminal side of
and the x-axis
be a nonacute angle in standard position that lies in a quadrant.
Example:
1.Find the reference angle, for each of the following angles:
4
7
a) b) =
c) d) = 3.6
= 210º
= -240º
2. Use the reference angles to find the exact value of the following
trigonometric functions:
4
5
tan 6
seca) sin 300º b) c)
15

16. 1.1.5: UNIT CIRCLE APPROACH; PROPERTIES
OF THE TRIGONOMETRIC FUNCTIONS
Definitions of the trigonometric functions in terms of a unit circle
If t is a real number and P = (x,y) is a point on the unit circle
that corresponds to t, then
ytsin xtcos 0,tan x
x
y
t
0,
1
csc y
y
t 0,
1
sec x
x
t 0,cot y
y
x
t
t
Example:
Find the values of the trigonometric function at
16

17. all real numbers. The range of these functions is the set of all
real numbers from -1 to 1, inclusive.
The domain and range of the sine and cosine functions
The domain of the sine function and the cosine function is the set of
tt cos)cos( tt sec)sec(
Even and odd trigonometric functions
The cosine and secant functions are even
tt sin)sin(
tt csc)csc(
tt tan)tan(
tt cot)cot(
The sine, cosecant, tangent and cotangent functions are odd
)60cos( 6
tan
Example:
Find the exact value of: a) b)
17

18. Definition of a periodic function
A function f is periodic if there exists a positive number p such that
)()( tfptf
for all t in the domain of f. The smallest number p for which f is periodic
is called the period of f
tt sin)2sin( tt cos)2cos(
2
Periodic properties of the sine and cosine functions
and
The sine and cosine functions are periodic functions and have period
tt tan)tan( tt cot)cot(
Periodic properties of tangent and cotangent functions
and
The tangent and cotangent functions are periodic functions and
have period
tnt sin)2sin( tnt cos)2cos( tnt tan)tan(
Repetitive behavior of the sine, cosine and tangent functions
For any integer n and real number t,
18

19. 1.1.6: Graphs of the Sine
and Cosine Functions
1 1y
Characteristics of the Sine Function:
Domain : all real numbers
Range :
2
sin)sin(
Period :
Symmetry through origin :
Odd function
x - intercepts : ...., , , , , , ,......2 0 2 3
y - intercept : 0
x ....., , , ,...
3
2 2
5
2
x ....., , , ,...
2
3
2
7
2
max value : 1 , occurs at
min value : -1 , occurs at
19

20. Graphing variations of y=sin x
Graph of y=A sin Bx
1.Identify the amplitude and the period
Amplitude = |A| ; Period =
B
2
2. Find the values of x
3. Find the values of y for the one that we find in step 2
4. Connect all the points and extend to the left or right as desired
Graph of y = A sin (Bx – C)
This graph is obtained by horizontally shifting the graph of y=A sin Bx so
that the starting point of the cycle is shifted from x = 0 to
B
C
x
This is called the phase shift
If 0
B
C
the shift is to the right
If 0
B
C
the shift is to the left
20

21. Example:
1- Determine the amplitude of y = 3sin x. Then graph y = sin x and y = 3sin x for
20 x
xy sin
2
1
xy sin xy sin
2
1
3x
2- Determine the amplitude of . Then graph and
for
xy
2
1
sin2
80 x
3- Determine the amplitude and period of . Then graph the function
for
4- Determine the amplitude, period, and phase shift of 32sin3 xy
Then graph one period of the function
21

22. Characteristics of the Cosine Function:
Domain : all real numbers
1 1y
2
cos( ) cos
Range :
Period :
Symmetry about y-axis :
Even function
x - intercepts : ....., , , , , ,...
3
2 2 2
3
2
5
2
y - intercept : 1
x ..., , , , ,......2 0 2 4
x ...., , , , ,......3 5
max value : 1 , occurs at
min value : -1 , occurs at
22

23. Graphing variations of y=cos x
Graph of y=A cos Bx
1.Identify the amplitude and the period
Amplitude = |A| ; Period =
B
2
2. Find the values of x
3. Find the values of y for the one that we find in step 2
4. Connect all the points and extend to the left or right as desired
B
C
x
Graph of y = A cos (Bx – C)
This graph is obtained by horizontally shifting the graph of y=A cos Bx so
that the starting point of the cycle is shifted from x = 0 to
This is called the phase shift
If 0
B
C
the shift is to the right
If 0
B
C
the shift is to the left
23

24. xy cos4
22 x
Example: Determine the amplitude and period of
Then graph the function for
Vertical shifts of sinusoidal graphs
For y = A sin (Bx – C) + D and y = A cos (Bx – C) +
D, the constant +D will cause the graph to shift
upward while –D will cause the graph to move
downward.
So, the max y is D + |A| and the min y is D - |A|
Example: Graph one period of the function y = 2 cos x + 1
24

25. 1.1.7: GRAPHS OF THE TANGENT,
COTANGENT, COSECANT, AND SECANT
FUNCTIONS
2
Characteristics of the Tangent Function:
Domain : all real numbers except odd multiples
tan( ) tan
Range : all real numbers
Period :
Symmetry with respect to the origin :
Odd function
x ..., , , , , , ,......2 0 2 3
x ....., , , , ,...
3
2 2 2
3
2
x - intercepts :
y - intercept : 0
Vertical asymptotes :
25

26. Characteristics of the Cotangent Function
Domain : all real numbers except integral multiples of
Range : all real numbers
Period :
cot)cot(
......2,,0,2,...,x
...2,,0,.....,x
Symmetry with respect to the origin :
x - intercepts :
y - intercept : none
Vertical asymptotes :
Odd function
26

27. Characteristics of the Cosecant Function:
1y 1y
2
Domain : all real numbers except integral multiples of
Range : all real numbers of y such that or
Period :
csc)csc(
...2,,0,.....,x
Symmetry with respect to the origin :
x - intercepts : none
y - intercept : none
Vertical asymptotes :
Odd function
27

28. Characteristics of the Secant Function:
2
1y 1y
2
Domain : all real numbers except odd multiples of
Range : all real numbers of y such that or
Period :
sec)sec(
x ....., , , , ,...
3
2 2 2
3
2
Symmetry with respect to y-axis:
x - intercepts : none
y - intercept : 1
Vertical asymptotes :
Even function
28