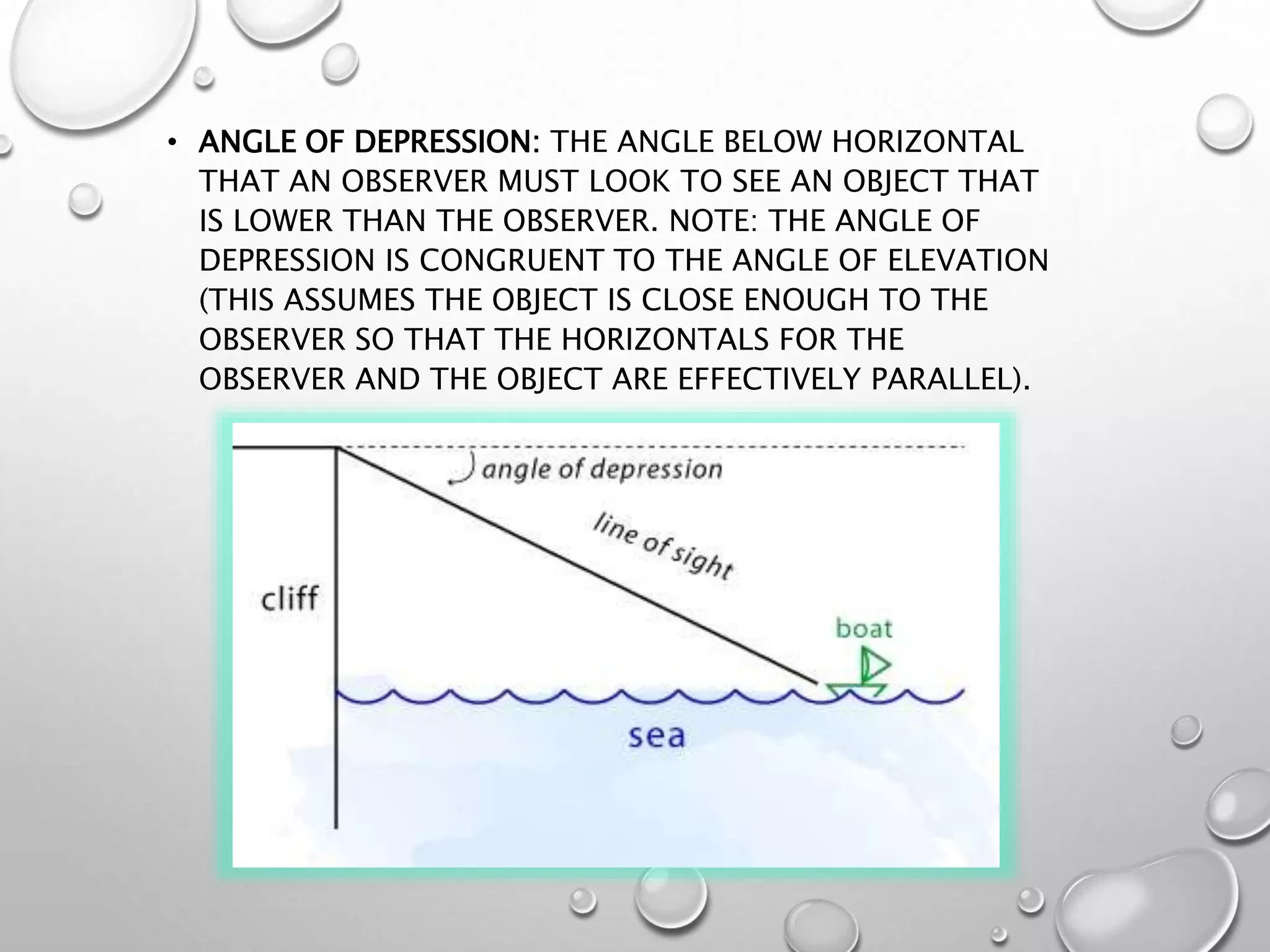
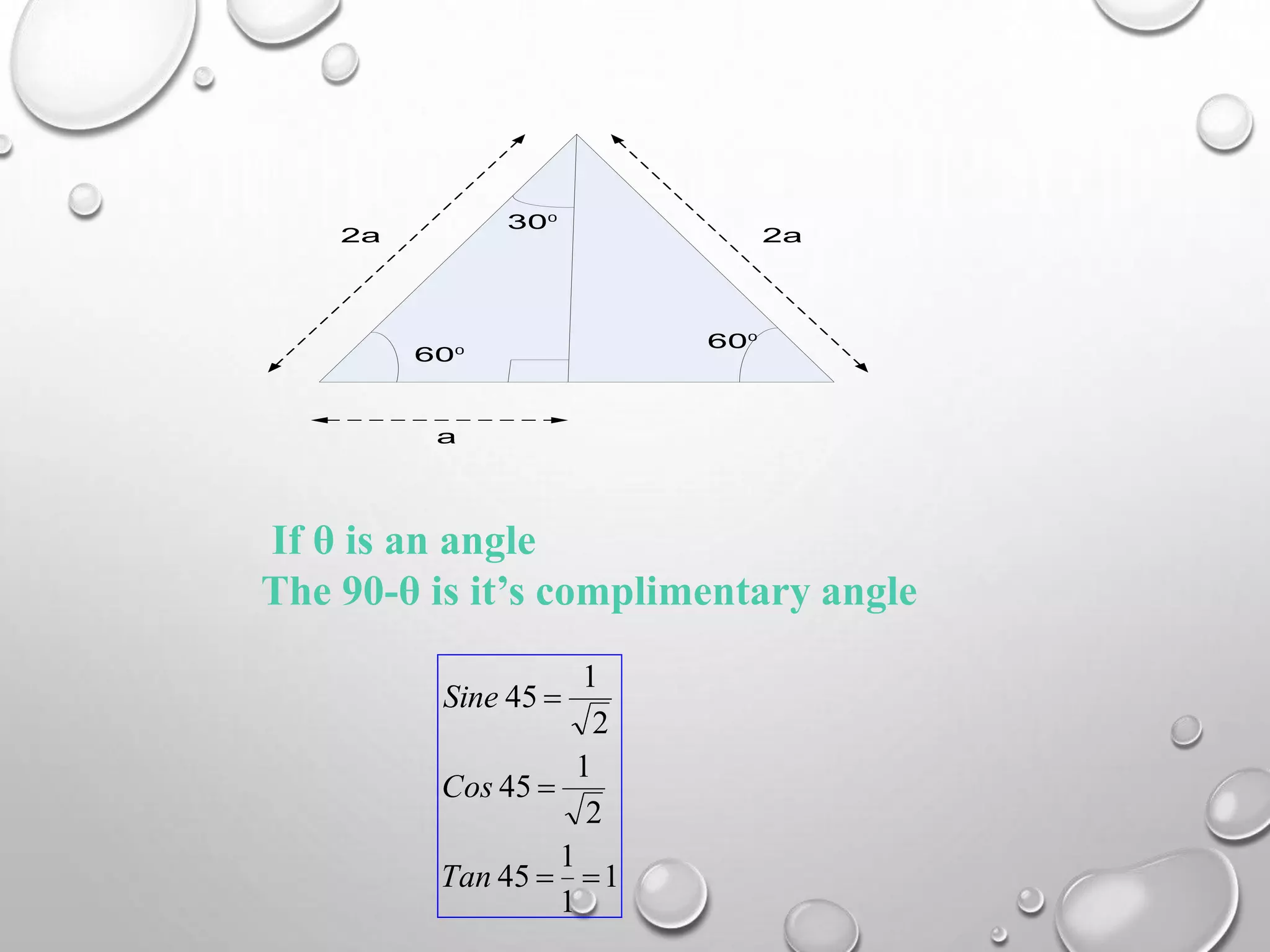
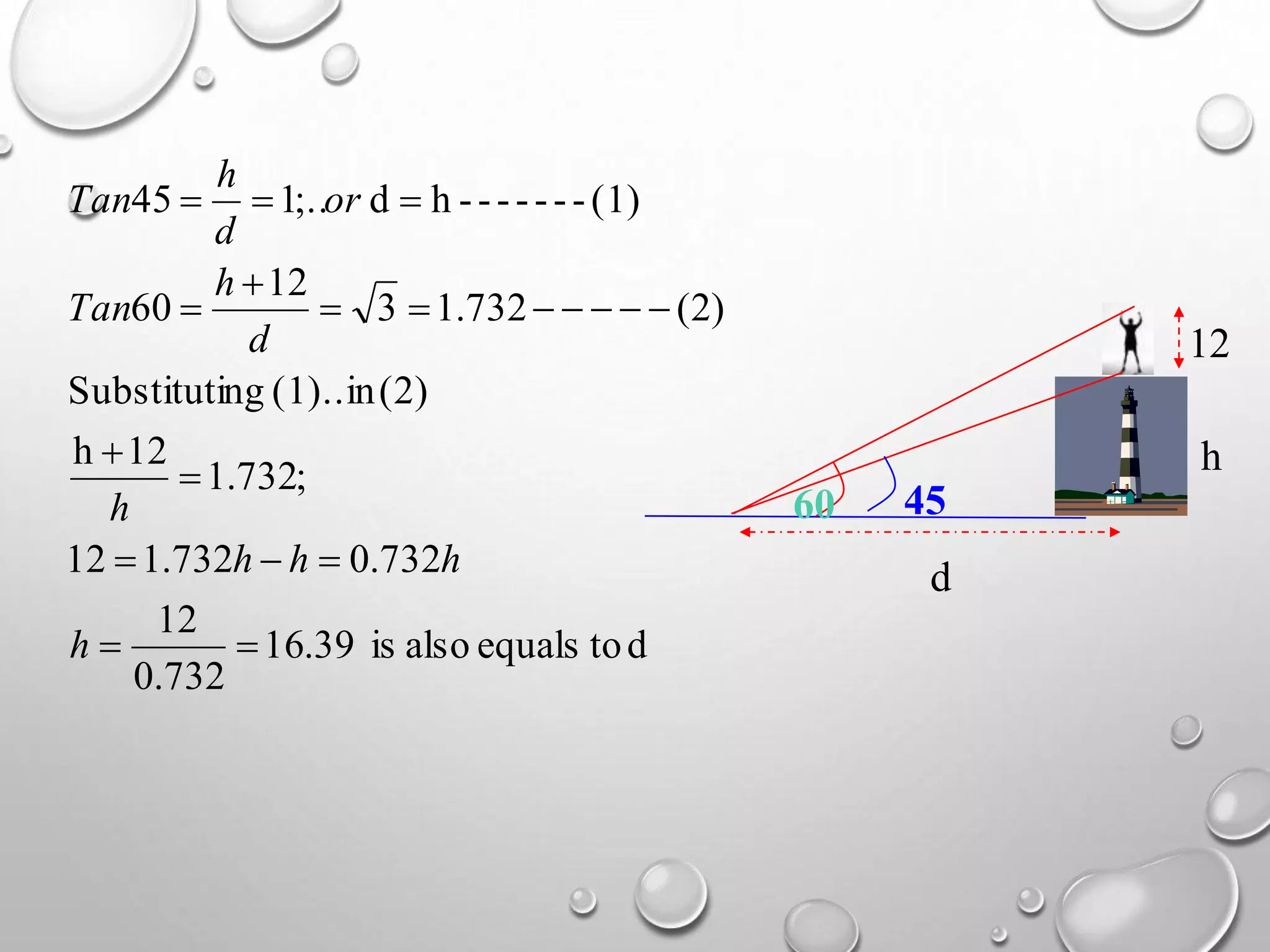
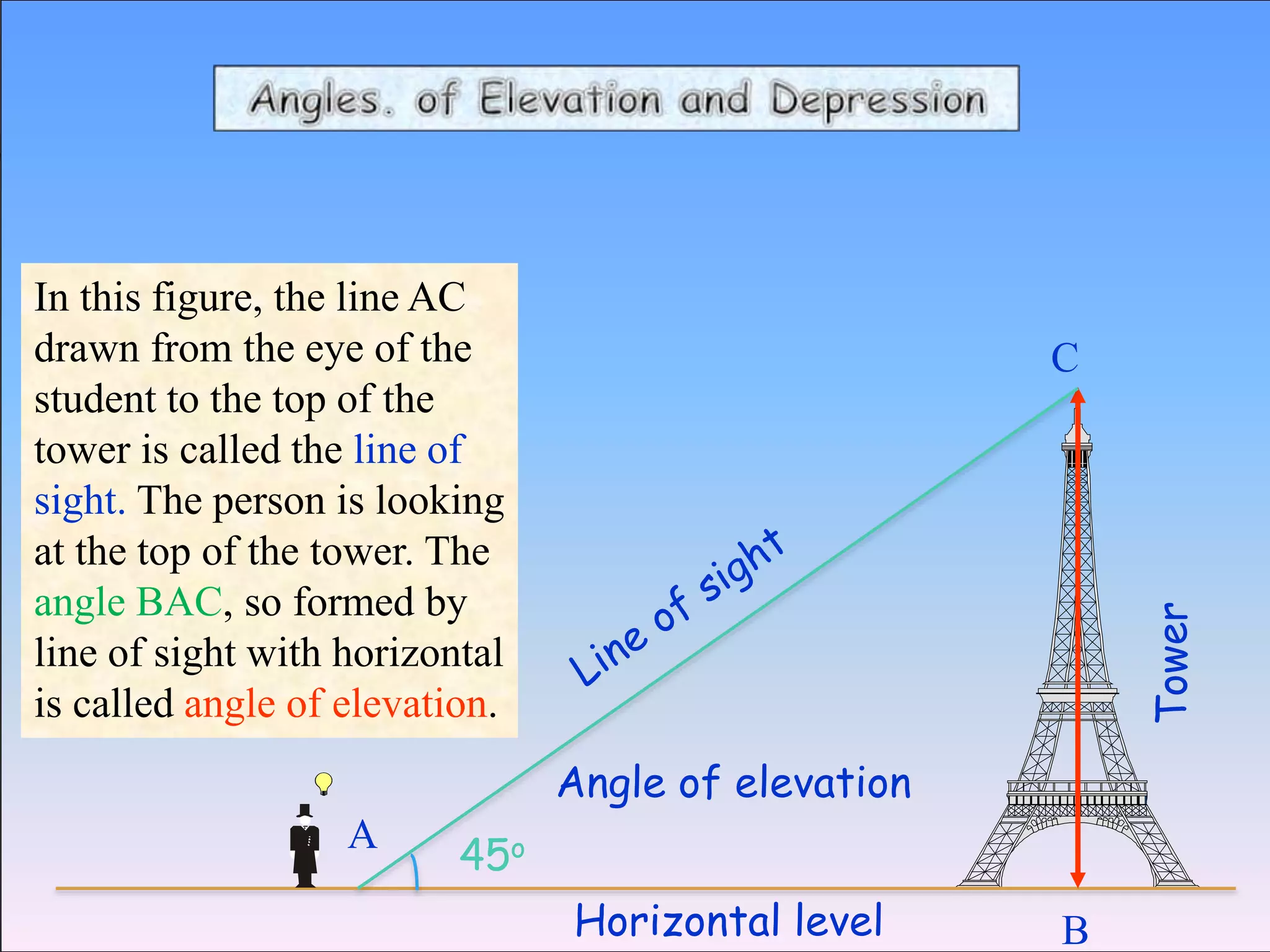
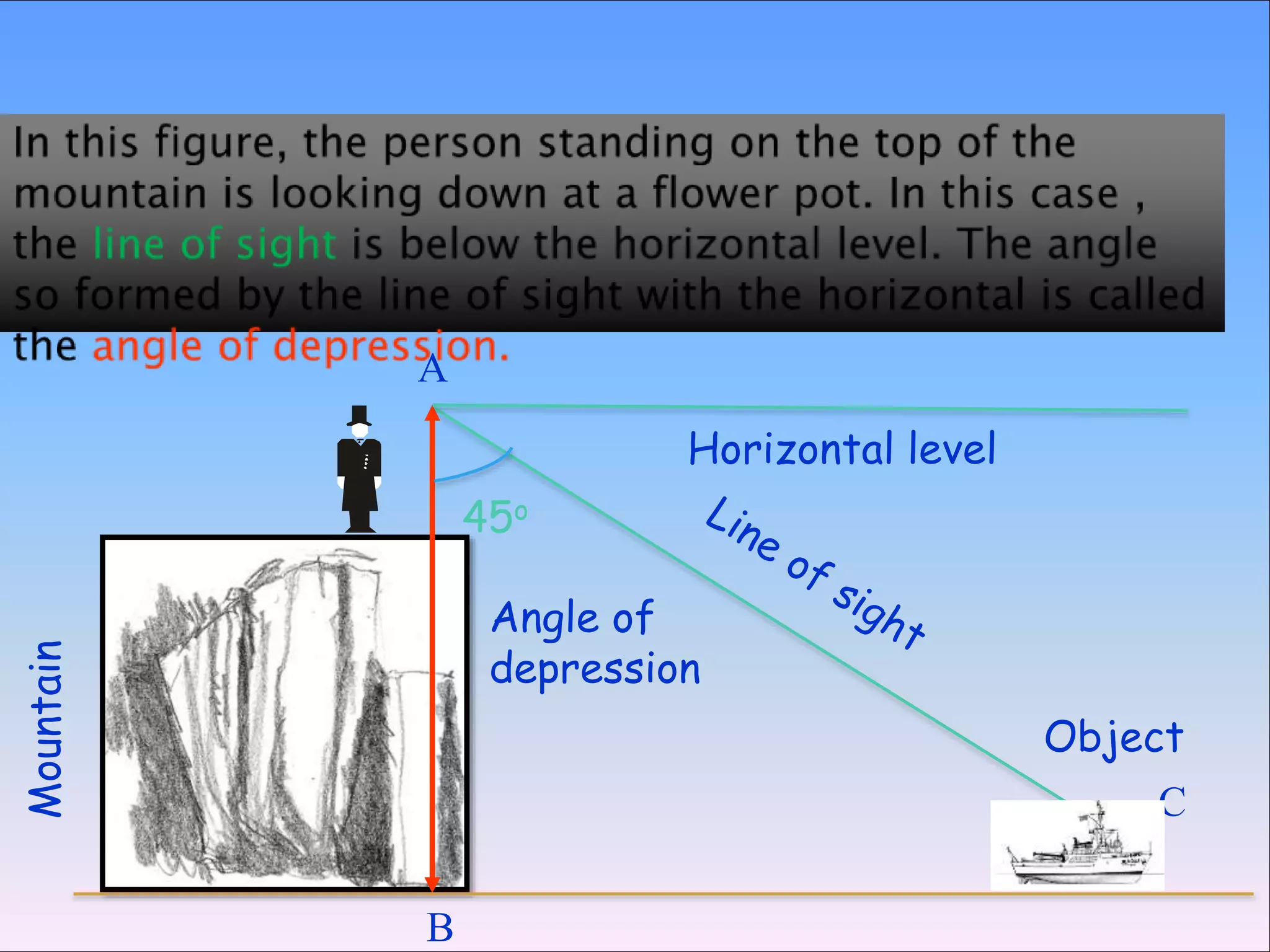
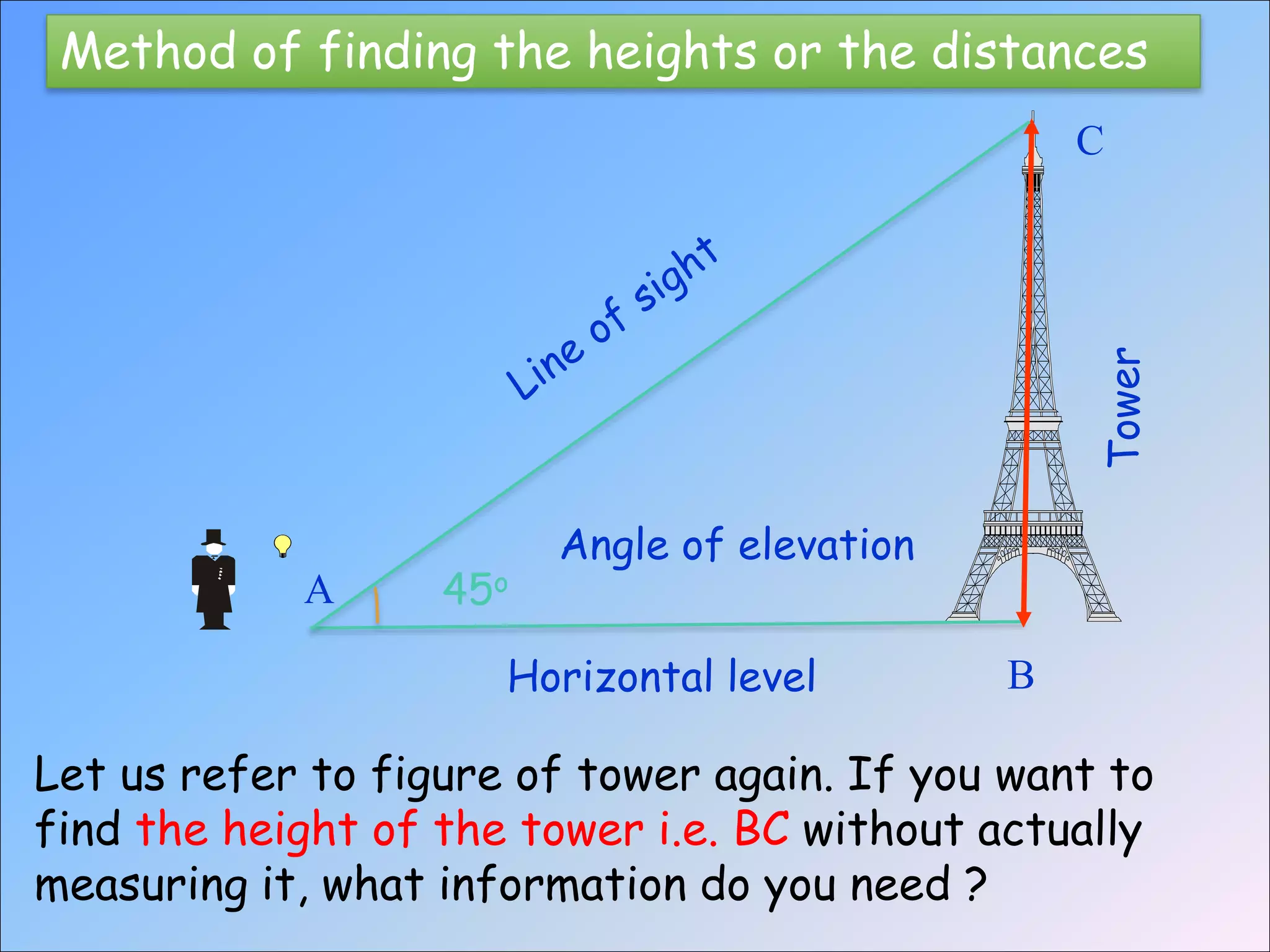
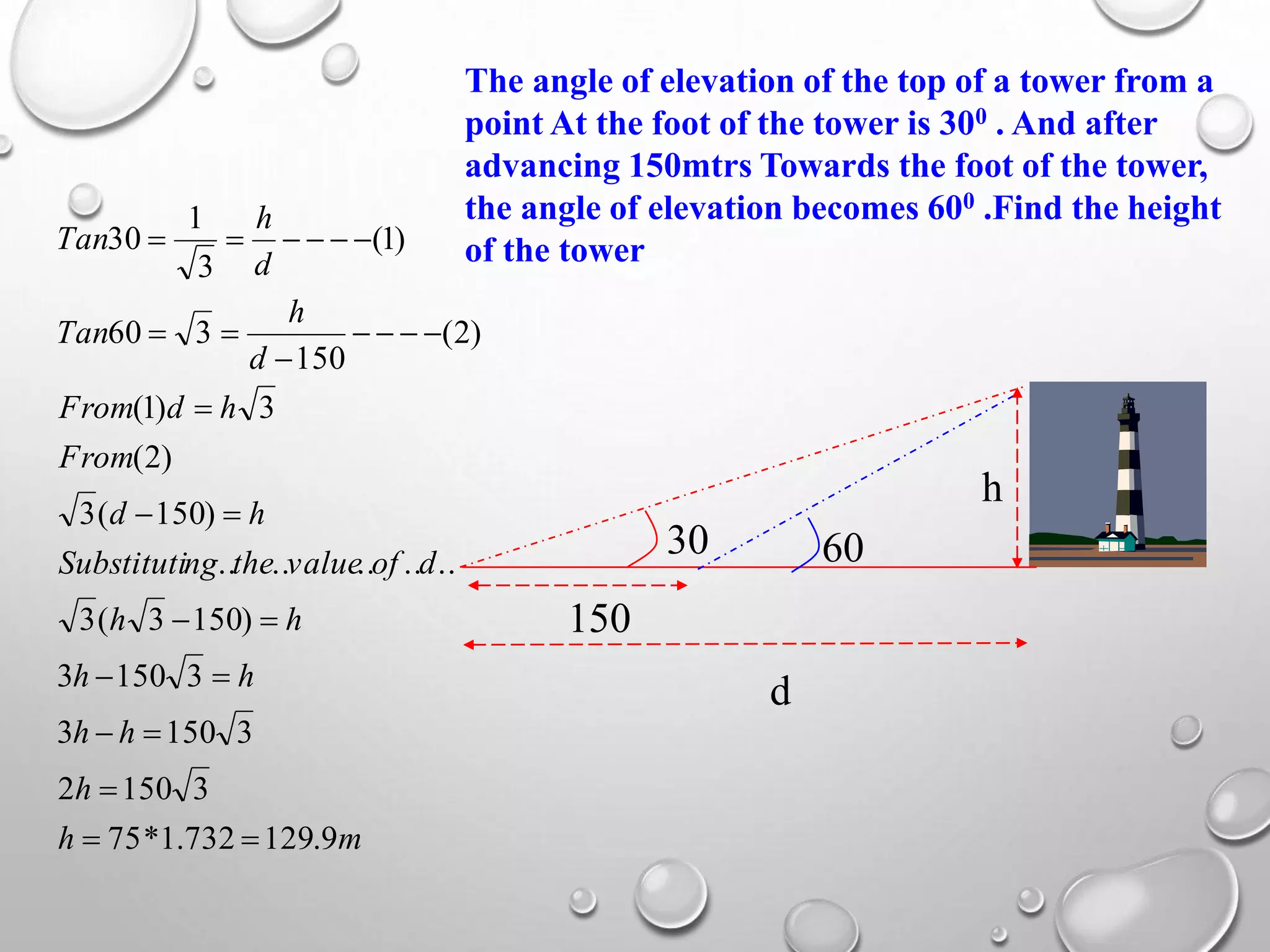
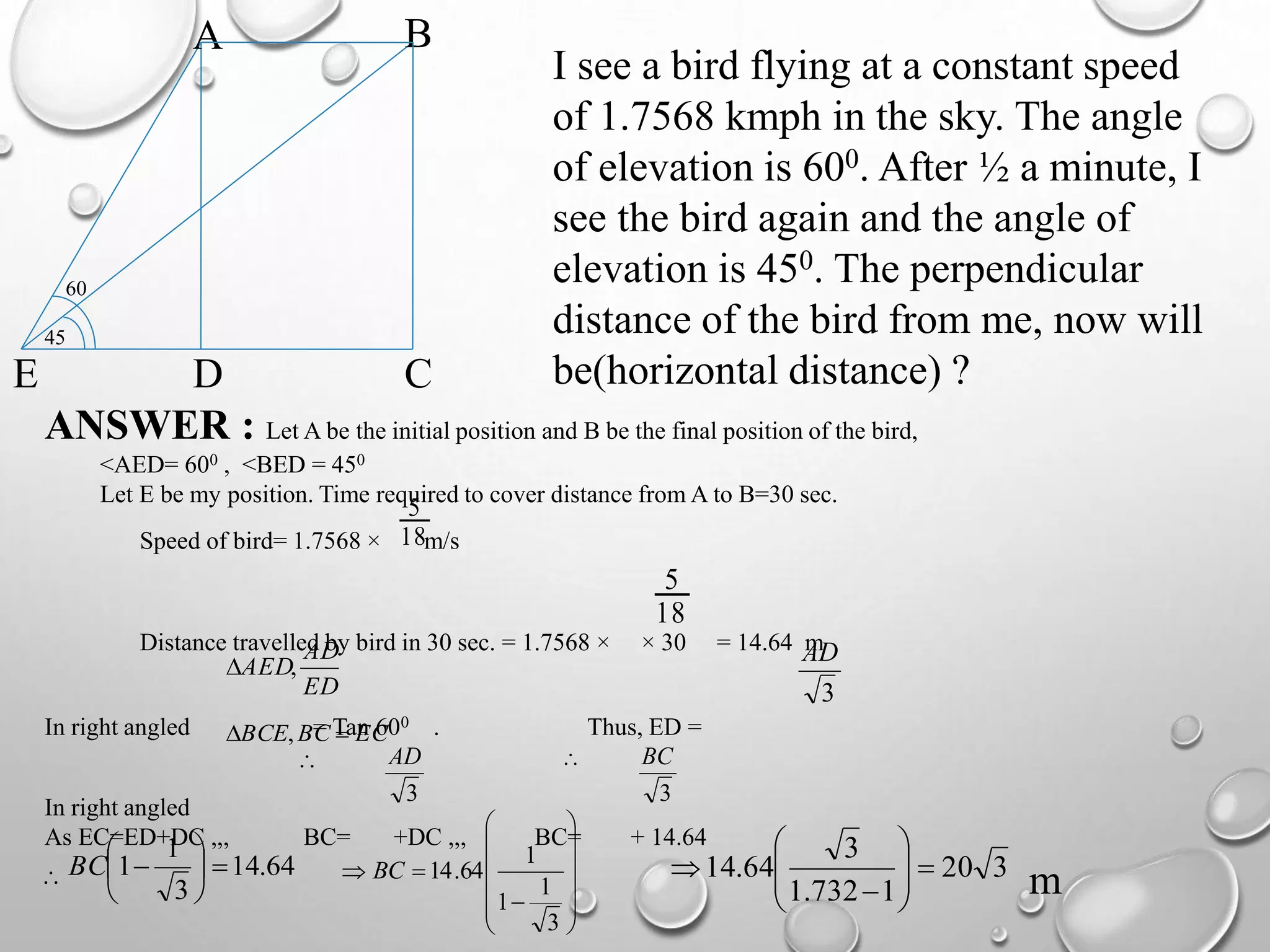
The document provides an overview of trigonometry, focusing on its applications in determining heights and distances involving right triangles. It explains key concepts such as angles of elevation and depression, and illustrates the relationships between various trigonometric functions. In particular, it highlights historical applications of trigonometry, including measuring the height of objects like the pyramids and its relevance in fields such as surveying and navigation.

1. MAHIP
SINGH
X-B
SOME APPLICATION OF
TRIGNOMETRY

2. INTRODUCTION
• TRIGONOMETRY IS THE BRANCH OF MATHEMATICS THAT DEALS
WITH TRIANGLES PARTICULARLY RIGHT TRIANGLES. FOR ONE
THING TRIGONOMETRY WORKS WITH ALL ANGLES AND NOT
JUST TRIANGLES. THEY ARE BEHIND HOW SOUND AND LIGHT
MOVE AND ARE ALSO INVOLVED IN OUR PERCEPTIONS OF
BEAUTY AND OTHER FACETS ON HOW OUR MIND WORKS. SO
TRIGONOMETRY TURNS OUT TO BE THE FUNDAMENTAL TO
PRETTY MUCH EVERYTHING

3. BASIC FUNDAMENTALS
• ANGLE OF ELEVATION: IN THE PICTURE
BELOW, AN OBSERVER IS STANDING AT THE
TOP OF A BUILDING IS LOOKING STRAIGHT
AHEAD (HORIZONTAL LINE). THE OBSERVER
MUST RAISE HIS EYES TO SEE THE AIRPLANE
(SLANTING LINE). THIS IS KNOWN AS THE
ANGLE OF ELEVATION.

4. • ANGLE OF DEPRESSION: THE ANGLE BELOW HORIZONTAL
THAT AN OBSERVER MUST LOOK TO SEE AN OBJECT THAT
IS LOWER THAN THE OBSERVER. NOTE: THE ANGLE OF
DEPRESSION IS CONGRUENT TO THE ANGLE OF ELEVATION
(THIS ASSUMES THE OBJECT IS CLOSE ENOUGH TO THE
OBSERVER SO THAT THE HORIZONTALS FOR THE
OBSERVER AND THE OBJECT ARE EFFECTIVELY PARALLEL).

5. 600
300
600
a
2a2a
If θ is an angle
The 90-θ is it’s complimentary angle
1
1
1
45
2
1
45
2
1
45



Tan
Cos
Sine

6. A trigonometric function is a ratio of certain parts of a triangle. The
names of these ratios are: The sine, cosine, tangent, cosecant, secant,
cotangent.
Let us look at this triangle…
a
c
b
ө A
B
C
Given the assigned letters to the sides and
angles, we can determine the following
trigonometric functions.
The Cosecant is the inversion of the
sine, the secant is the inversion of
the cosine, the cotangent is the
inversion of the tangent.
With this, we can find the sine of the
value of angle A by dividing side a
by side c. In order to find the angle
itself, we must take the sine of the
angle and invert it (in other words,
find the cosecant of the sine of the
angle).
Sinθ=
Cos θ=
Tan θ=
Side Opposite
Side Adjacent
Side Adjacent
Side Opposite
Hypothenuse
Hypothenuse
=
=
= a
b
c
a
b
c
BY- MAHIP SINGH X-BBY-MAHIP SINGH X-B

7. 4560
12
h
d
dtoequalsalsois39.16
732.0
12
732.0732.112
;732.1
12h
(2)(1)..inngSubstituti
)2(732.13
12
60
(1)-------hd;..145








h
hhh
h
d
h
Tan
or
d
h
Tan

8. The angle of elevation of the top of a tower from a
point At the foot of the tower is 300 . And after
advancing 150mtrs Towards the foot of the tower,
the angle of elevation becomes 600 .Find the height
of the tower
150
h
d
30 60
mh
h
hh
hh
hh
dofvaluethengSubstituti
hd
From
hdFrom
d
h
Tan
d
h
Tan
9.129732.1*75
31502
31503
31503
)1503(3
..........
)150(3
)2(
3)1(
)2(
150
360
)1(
3
1
30












9. ?
45o
?
What you’re
going to do
next?
Heights and
Distances

10. In this situation , the distance or the heights can
be founded by using mathematical techniques,
which comes under a branch of ‘trigonometry’.
The word ‘ trigonometry’ is derived from the
Greek word ‘tri’ meaning three , ‘gon’ meaning
sides and ‘metron’ meaning measures.
Trigonometry is concerned with the relationship
between the angles and sides of triangles. An
understanding of these relationships enables
unknown angles and sides to be calculated
without recourse to direct measurement.
Applications include finding heights/distances of
objects.

13. Sun’s rays casting shadows mid-afternoon Sun’s rays casting shadows late afternoon
An early application of trigonometry was made by Thales on a
visit to Egypt. He was surprised that no one could tell him the
height of the 2000 year old Cheops pyramid. He used his
knowledge of the relationship between the heights of objects
and the length of their shadows to calculate the height for
them. (This will later become the Tangent ratio.) Can you see what
this relationship is, based on the drawings below?
Thales of Miletus
640 – 546 B.C. The
first Greek
Mathematician. He
predicted the Solar
Eclipse of 585 BC.
Trigonometry
Similar
Triangles
Similar
Triangles
Thales may not have used similar triangles directly to solve the problem but
he knew that the ratio of the vertical to horizontal sides of each triangle was
constant and unchanging for different heights of the sun. Can you use the
measurements shown above to find the height of Cheops?
6 ft
9 ft
720 ft
h
6
720 9
h

480 ft
(Egyptian feet of course)4
6 720
9
80 ft
x
h  

14. h
Early Applications of Trigonometry
Finding the height of a
mountain/hill.
Finding the distance to
the moon.
Constructing sundials to
estimate the time from
the sun’s shadow.

15. Historically trigonometry was developed for work
in Astronomy and Geography. Today it is used
extensively in mathematics and many other areas
of the sciences.
•Surveying
•Navigation
•Physics
•Engineering

16. 45o
Angle of elevation
A
C
B
In this figure, the line AC
drawn from the eye of the
student to the top of the
tower is called the line of
sight. The person is looking
at the top of the tower. The
angle BAC, so formed by
line of sight with horizontal
is called angle of elevation.
Tower
Horizontal level

17. 45o
Mountain
Angle of
depression
A
B
C
Object
Horizontal level

18. 45o
Angle of elevation
A
C
B
Tower
Horizontal level
Method of finding the heights or the distances
Let us refer to figure of tower again. If you want to
find the height of the tower i.e. BC without actually
measuring it, what information do you need ?

19. We would need to know the following:
i. The distance AB which is the distance between
tower and the person .
ii. The angle of elevation angle BAC .
Assuming that the above two conditions are given
then how can we determine the height of the
height of the tower ?
In ∆ABC, the side BC is the opposite side in
relation to the known angle A. Now, which of the
trigonometric ratios can we use ? Which one of
them has the two values that we have and the one
we need to determine ? Our search narrows down
to using either tan A or cot A, as these ratios
involve AB and BC.
Therefore, tan A = BC/AB or cot A = AB/BC,
which on solving would give us BC i.e., the height of
the tower.

20. The angle of elevation of the top of a tower from a
point At the foot of the tower is 300 . And after
advancing 150mtrs Towards the foot of the tower,
the angle of elevation becomes 600 .Find the height
of the tower
150
h
d
30 60
mh
h
hh
hh
hh
dofvaluethengSubstituti
hd
From
hdFrom
d
h
Tan
d
h
Tan
9.129732.1*75
31502
31503
31503
)1503(3
..........
)150(3
)2(
3)1(
)2(
150
360
)1(
3
1
30












21. 45
BA
CDE
60
I see a bird flying at a constant speed
of 1.7568 kmph in the sky. The angle
of elevation is 600. After ½ a minute, I
see the bird again and the angle of
elevation is 450. The perpendicular
distance of the bird from me, now will
be(horizontal distance) ?
ANSWER : Let A be the initial position and B be the final position of the bird,
<AED= 600 , <BED = 450
Let E be my position. Time required to cover distance from A to B=30 sec.
Speed of bird= 1.7568 × m/s
Distance travelled by bird in 30 sec. = 1.7568 × × 30 = 14.64 m
In right angled = Tan 600 . Thus, ED =
In right angled
As EC=ED+DC ,,, BC= +DC ,,, BC= + 14.64
18
5
18
5
ED
AD
AED,
3
AD
ECBCBCE  ,

3
AD 
3
BC
 64.14
3
1
1 





BC














3
1
1
1
64.14BC 320
1732.1
3
64.14 









m

22. Thank you
BY- MAHIP SINGH X-BX-B