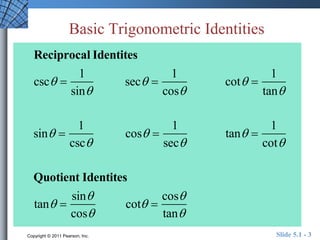
The document discusses trigonometric identities that are important for working with trigonometric functions in calculus. It covers basic identities like reciprocal, quotient, Pythagorean, cofunction, and odd-even identities. Examples are provided of using identities to simplify expressions and solve trigonometric equations.

1. 5.1
Fundamental
Identities
Copyright © 2011 Pearson, Inc.

2. What you’ll learn about
 Identities
 Basic Trigonometric Identities
 Pythagorean Identities
 Cofunction Identities
 Odd-Even Identities
 Simplifying Trigonometric Expressions
 Solving Trigonometric Equations
… and why
Identities are important when working with trigonometric
functions in calculus.
Copyright © 2011 Pearson, Inc. Slide 5.1 - 2

3. Basic Trigonometric Identities
Reciprocal Identites
csc 
1
sin
sec 
1
cos
cot 
1
tan
sin 
1
csc
cos 
1
sec
tan 
1
cot
Quotient Identites
tan 
sin
cos
cot 
cos
tan
Copyright © 2011 Pearson, Inc. Slide 5.1 - 3

4. Pythagorean Identities
2 2
cos sin 1
1 tan sec
cot 1 csc
 
 
2 2
 
 
2 2
  

Copyright © 2011 Pearson, Inc. Slide 5.1 - 4

5. Example Using Identities
Find sin and cos if tan  3 and cos  0.
Copyright © 2011 Pearson, Inc. Slide 5.1 - 5

6. Example Using Identities
Find sin and cos if tan  3 and cos  0.
To find sin , use tan  3
and cos  1 / 10.
tan 
sin
cos
sin  cos tan
sin  1 / 103
sin  3 / 10
1 tan2  sec2
1 9  sec2
sec   10
cos  1 / 10
Therefore, cos  1/ 10 and sin  3/ 10
Copyright © 2011 Pearson, Inc. Slide 5.1 - 6

7. Cofunction Identities
Angle A: sin A 
y
r
tan A 
y
x
secA 
r
x
cosA 
x
r
cot A 
x
y
cscA 
r
y
Angle B: sin B 
x
r
tan B 
x
y
secB 
r
y
cosB 
y
r
cot B 
y
x
cscB 
r
x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 7

8. Cofunction Identities
 
   
       
   
   
       
   
   
       
   
sin cos cos sin
   
2 2
 
tan cot cot tan
   
2 2
 
sec csc csc sec
   
2 2
Copyright © 2011 Pearson, Inc. Slide 5.1 - 8

9. Even-Odd Identities
sin(x)   sin x cos(x)  cos x tan(x)   tan x
csc(x)   csc x sec(x)  sec x cot(x)   cot x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 9

10. Example Simplifying by Factoring
and Using Identities
Simplify the expression cos3 x  cos x sin2 x.
Copyright © 2011 Pearson, Inc. Slide 5.1 - 10

11. Example Simplifying by Factoring
and Using Identities
Simplify the expression cos3 x  cos x sin2 x.
cos3 x  cos xsin2 x  cos x(cos2 x  sin2 x)
 cos x(1) Pythagorean Identity
 cos x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 11

12. Example Simplifying by Expanding
and Using Identities
Simplify the expression:
csc x -1csc x 1
cos2 x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 12

13. Example Simplifying by Expanding
and Using Identities
csc x 1csc x 1
cos2 x

csc2 x 1
cos2 x
(a  b)(a  b)  a2  b2

cot2 x
cos2 x
Pythagorean Identity

cos2 x
sin2 x

1
cos2 x
cot 
cos
sin
1

sin2 x
 csc2 x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 13

14. Example Solving a Trigonometric
Equation
Find all values of x in the interval 0,2 
that solve
sin3 x
cos x
 tan x.
Copyright © 2011 Pearson, Inc. Slide 5.1 - 14

15. Example Solving a Trigonometric
Equation
sin3 x
cos x
 tan x
sin3 x
cos x

sin x
cos x
Reject the posibility that cos2 x  0
because it would make both
sides of the original equation
undefined. sin x  0 in the interval
0  x  2 when x  0 and x   .
sin3 x  sin x
sin3 x  sin x  0
sin x(sin2 x 1)  0
sin x cos2  x 0
sin x  0 or cos2 x  0
Copyright © 2011 Pearson, Inc. Slide 5.1 - 15

16. Quick Review
Evaluate the expression.
1. sin1 4
5

 

 

2. cos1 
12
13
 

 
Factor the expression into a product of linear factors.
3. 2a2  3ab  2b2
4. 9u2  6u 1
Simplify the expression.
5.
2
y

3
x
Copyright © 2011 Pearson, Inc. Slide 5.1 - 16

17. Quick Review Solutions
Evaluate the expression.
1. sin1 4
5

 

 
53.13o  0.927 rad

2. cos1 
12
13
 

 
157.38o  2.747 rad
Factor the expression into a product of linear factors.
3. 2a2  3ab  2b2 2a  ba  2b
4. 9u2  6u 1 3u 12
Simplify the expression.
5.
2
y

3
x
2x  3y
xy
Copyright © 2011 Pearson, Inc. Slide 5.1 - 17