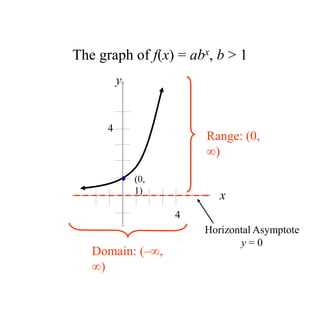
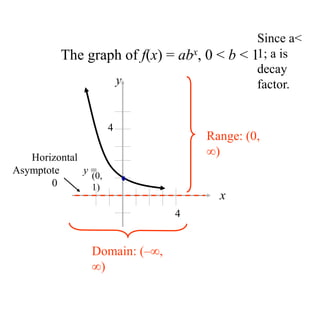
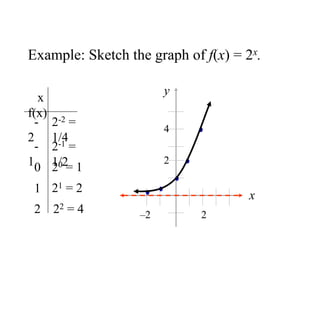
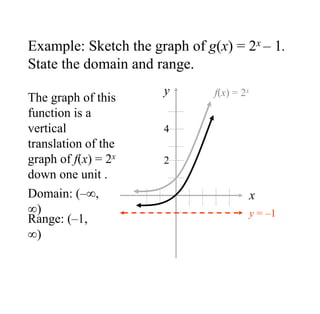
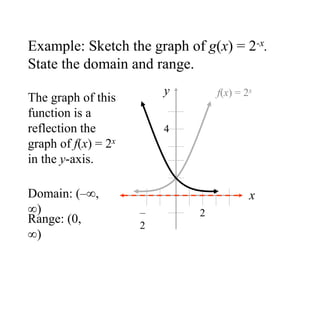
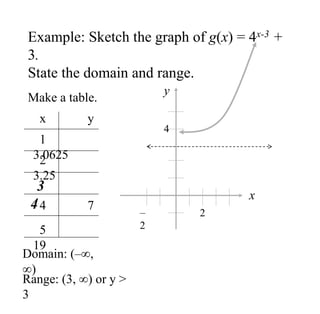
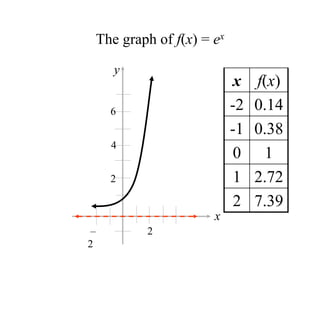
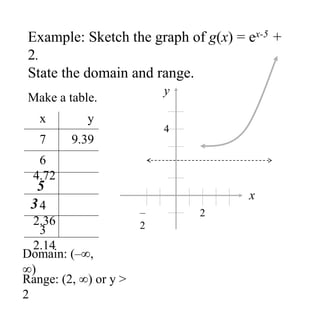
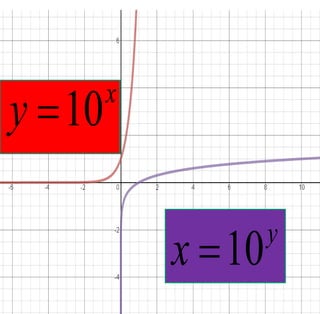
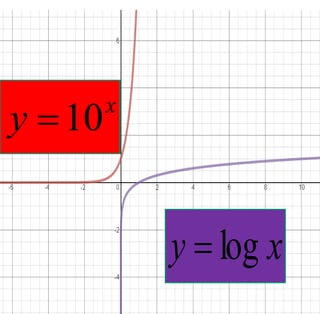
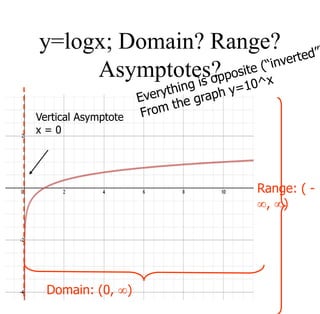
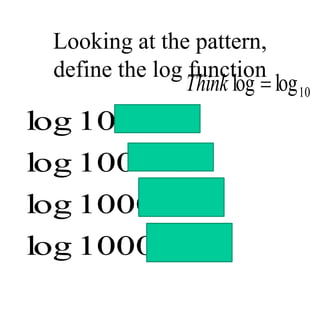
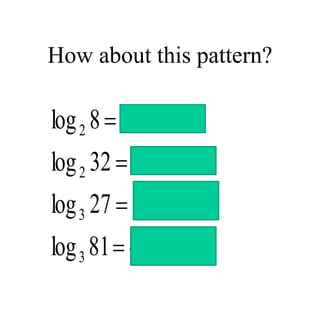
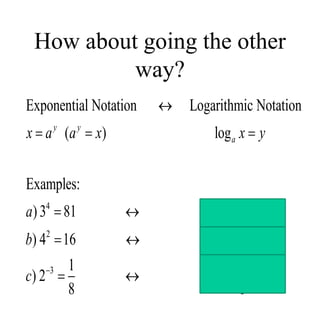
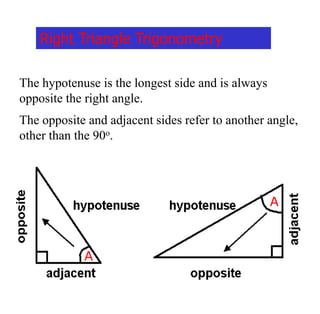
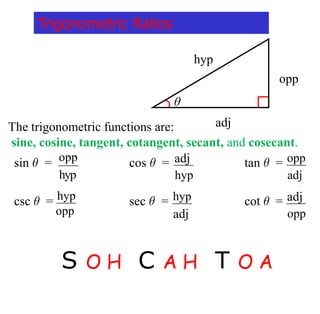
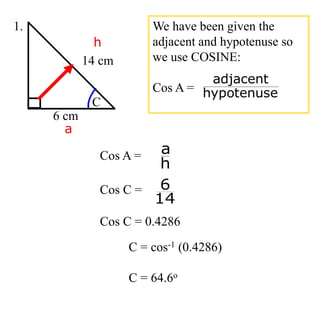
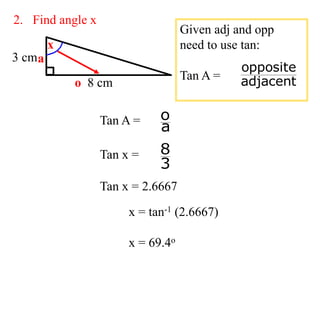
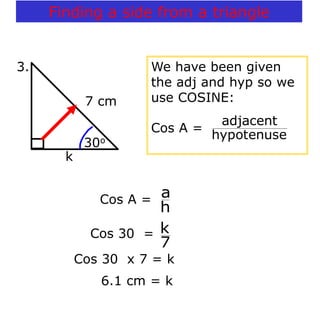
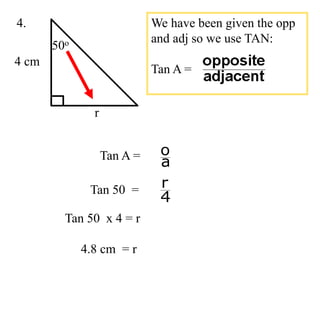
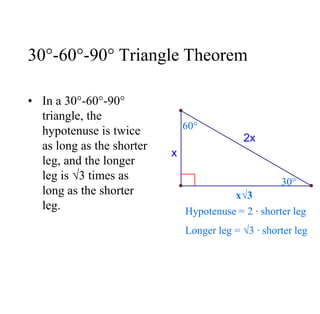
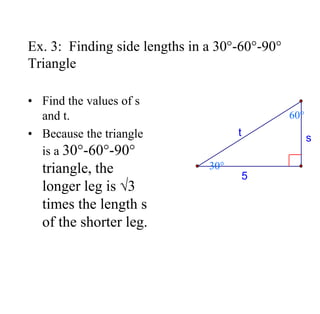
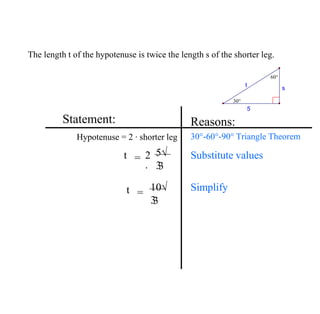
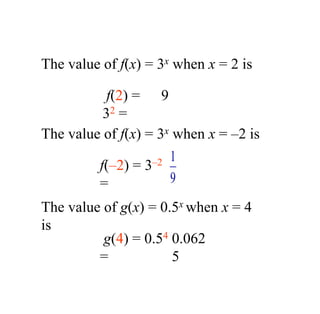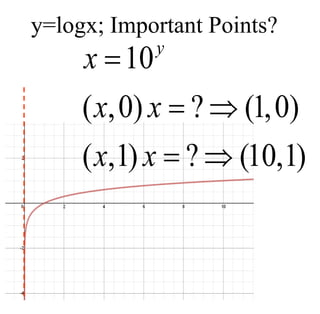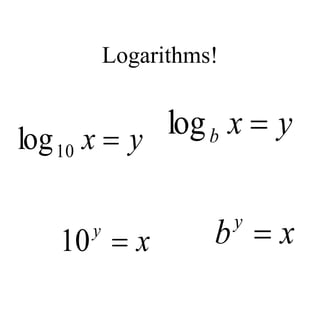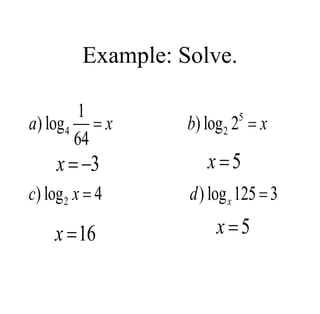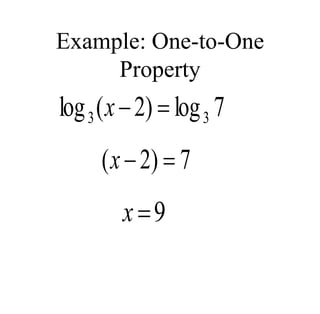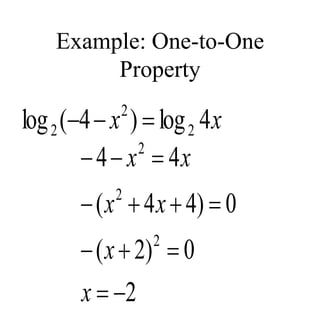The document covers exponential and logarithmic functions, detailing definitions, graphs, properties, and examples of calculations involving these functions. It explains how to derive exponential equations from given points and provides techniques for solving logarithmic equations using the inverse relationship between exponentiation and logarithms. Additionally, the document touches on the basics of trigonometry, including definitions of trigonometric functions and theorems related to right triangles.

1. 2.7.1.Exponential Functions
and Their Graphs

2. The exponential function f with base b
is defined by
f(x) = abx
where b > 0, b  1, and x is any real
number.
** when b> 1; b is considered a growth
factor.
For instance,
f(x) = 3x and g(x) = 0.5x
are exponential functions.

3. The value of f(x) = 3x when x = 2 is
f(2) =
32 =
The value of g(x) = 0.5x when x = 4
is
g(4) = 0.54
=
The value of f(x) = 3x when x = –2 is
9
1
9
f(–2) = 3–2
=
0.062
5

4. The graph of f(x) = abx, b > 1
y
x
(0,
1)
Domain: (–,
)
Range: (0,
)
Horizontal Asymptote
y = 0
4
4

5. The graph of f(x) = abx, 0 < b < 1
y
x
(0,
1)
Domain: (–,
)
Range: (0,
)
Horizontal
Asymptote y =
0
4
4
Since a<
1; a is
decay
factor.

6. Example: Sketch the graph of f(x) = 2x.
x
y
2
–2
2
4
x
f(x)
-
2
-
10
1
2
2-2 =
1/4
2-1 =
1/2
20 = 1
21 = 2
22 = 4

7. Example: Sketch the graph of g(x) = 2x – 1.
State the domain and range.
x
y
The graph of this
function is a
vertical
translation of the
graph of f(x) = 2x
down one unit .
f(x) = 2x
y = –1
Domain: (–,
)
Range: (–1,
)
2
4

8. Example: Sketch the graph of g(x) = 2-x.
State the domain and range.
x
y
The graph of this
function is a
reflection the
graph of f(x) = 2x
in the y-axis.
f(x) = 2x
Domain: (–,
)
Range: (0,
)
2
–
2
4

9. Example: Sketch the graph of g(x) = 4x-3 +
3.
State the domain and range.
x
y
Make a table.
Domain: (–,
)
Range: (3, ) or y >
3
2
–
2
4
x y
3
4
2
3.25
1
3.0625
4 7
5
19

10. Write an exponential function y =
abx for the graph that includes the
given points.
(2, 2) and (3,
4)
y = abx Substitute in (2,2) for x
and y.
2 = ab2
Solve for a
2 = a
b2
Now substitute (3,4) in for x and y into y =
abx
4 = ab3
b3
4 = a
b3
Set them equal to each other:
2 = 4 = a
b3 b2
Now solve for b to get b=2
You must solve for a: 2/2^2 = (1/2) =
a
Subst you’re a = (1/2) & b = 2 into
either one of your 2 equations: y =
abx
Y = (1/2)(2)^x

11. Write an exponential function y = abx for
the graph that includes the given points.
(2, 4) and (3,
16)
y = abx

12. The irrational number e, where
e  2.718281828…
is used in applications involving
growth and decay.
Using techniques of calculus, it can be
shown that









 n
e
n
n
as
1
1
The Natural Base e

13. The graph of f(x) = ex
y
x
2
–
2
2
4
6
x f(x)
-2 0.14
-1 0.38
0 1
1 2.72
2 7.39

14. Example: Sketch the graph of g(x) = ex-5 +
2.
State the domain and range.
x
y
Make a table.
Domain: (–,
)
Range: (2, ) or y >
2
2
–
2
4
x y
5
3
6
4.72
7 9.39
4
2.36
3
2.14

15. One to One Property
Copyright © by
Houghton Mifflin
Company, Inc. All rights
reserved.
If the bases are the same, then set the exponents
equal.
Example
—
3x = 32
x = ___
Example
—
3x+ 1 = 9
x = ___
Example
—
2x - 1 =
1/32
x = ___
Example—
e3x + 2 = e3
x = ___

16. 2.7.2. Logarithmic Functions
and Their Graphs

17. Use graph paper
• Graph
• Then graph it’s inverse below it –
how can we find this?
• Switch x and y coordinates
• The inverse of is
• Graph the inverse in it’s current
form before we move on
x
y 10

x
y 10
 y
x 10


18. x
y 10

y
x 10


19. Logarithmic
• The inverse of is
• We need a new operation to solve for y
• Let’s make up some operation that is th
inverse of raising 10 to the power of an
exponent. Call it “Clifton”
x
y 10
 y
x 10

y
x 10

y
Clifton
x
Clifton 10

x
Clifton
y 
y
x
Clifton 

20. Logarithmic
• The actual inverse
operation of raising 10
to the power of an
exponent is to take the
logarithm.
• So is
equivalent to
y
x 10

x
y
y
x
x y
log
log
10
log
log



y
x 10

x
y log


21. y=logx; Important Points?
)
1
,
10
(
?
)
1
,
(
)
0
,
1
(
?
)
0
,
(
10





x
x
x
x
x y

22. x
y 10

x
y log


23. y=logx; Domain? Range?
Asymptotes?
Domain: (0, )
Range: ( -
, )
Vertical Asymptote
x = 0

24. Logarithms!
x
y
x
y


10
log10
x
b
y
x
y
b


log

25. Common Logarithm: Base
10
10
2
0.3979
log common logarithm
log is understood to be base 10
when no other baseis written.
log100 = 2 10 100
log 2.5 0.3979 10 2.5

 
  

log

26. Logarithms, Explained -
Steve Kelly
• http://www.youtube.com/watch?v=z
zu2POfYv0Y

27. Looking at the pattern,
define the log function
4
10000
log
3
1000
log
2
100
log
1
10
log




10
log
log 
Think

28. How about this pattern?
4
81
log
3
27
log
5
32
log
3
8
log
3
3
2
2





29. So logarithms are just another helpful
way to write exponential equations
256
4
4
256
log
243
3
5
243
log
4
4
5
3







30. Mental Math Time
2
3
5
10
Express in exponential form.
) log 8 3
) log 9 2
1
) log 3
125
) log 0.1 1
a
b
c
d


 
 

31. How about going the other
way?
4
3
2
4
3
2
Exponential Notation Logarithmic Notation
( ) log
Examples:
) 3 81 log 81 4
) 4 16 log 16 2
1 1
) 2 log 3
8 8
y y
a
x a a x x y
a
b
c 

  
  
  
   

32. Example: Evaluate
5
2
8
) log 125
) log 16
) log 64
a
b
c
3
125
log
;
125
5 5
?


4
16
log
;
16
2 2
?


2
64
log
;
64
8 8
?



33. Example: Solve then write
in logarithmic form.
4
3
2
5
4
3
3
Express in logarithmic form.
) 2 16
) 4 64
1
)32
4
)3 3 3
a
b
c
d





4
16
log2 
3
4
)
3
3
(
log 3
3 
3
64
log4 
5
2
4
1
log32 


34. Natural Logarithm: Base e
e
0.6931
1.2040
log is written as ln x
read as"the natural log of x"
ln 2 = 0.6931 e 2
ln 0.3 1.2040 0.3
ln 5 5 1.609
x
e
x e x

 
   
    
6931
.
0
2
log 
e
Think

35. Graph the following
functions on the same axes
(pg 2 of packet)
• Rewrite as an exponential function.
• Plug in y-value first, then find x
• Don’t use a calculator!
• Record the domain, range and
asymptotes for each function
x
y
x
y
x
y
ln
log
log2




36. Graph the following
3
ln
)
2
(
log
)
1
log(
2






x
y
x
y
x
y
Desmos.com
1.Parent Function
2.Important Points of P.F.
3.Non-rigid Transformations – new points
4.Rigid Transformations – new points

37. Calculators:
• Calculator (Ti84+ and below) will only
compute common logs (base 10) and
natural logs (base e)!

38. Properties of Logarithms
0
1
log
1. log 1 0 because 1
2. log 1 because
3. log
4. log log , then
a
a
a
x
x
a
a a
a
a a
i
a
a x and a x
x y
nverse prop
x
erty
one to one property
y
 
 
 
  


39. Properties of Natural Logs
0
1
ln
1. ln1 0 because 1
2. ln 1 because
3. ln
4. ln ln , then
x x
inverse property
one to one property
e
e e e
e x and e x
x y x y
 
 
 
 
 

40. • We will get practice using these
properties in the next lessons.

41. H Dub:
• Pg 1 and 2 – bottom half
• Pg 3 – #”3”-5
• Pg 4 – #11-18
• 3-2 Pg. 236 #1-19odd, 27-44,
76-83, 87

42. Solving Logarithms:
• Rewrite in exponential form
• Solve for unknown
3
2
log 9
3 9
3 3
2
x
x
x
x





43. Example: Solve.
5
4 2
2
1
) log ) log 2
64
) log 4 ) log 125 3
x
a x b x
c x d
 
 
3


x 5

x
16

x 5

x

44. Example: One-to-One
Property
7
log
)
2
(
log 3
3 

x
7
)
2
( 

x
9

x

45. Example: One-to-One
Property
x
x 4
log
)
4
(
log 2
2
2 


2
0
)
2
(
0
)
4
4
(
4
4
2
2
2












x
x
x
x
x
x

46. Right Triangle Trigonometry
Trigonometry is based upon ratios of the sides of
right triangles.
The six trigonometric functions of a right triangle,
with an acute angle , are defined by ratios of two sides
of the triangle.
θ
opp
hyp
adj
The sides of the right triangle are:
 the side opposite the acute angle ,
 the side adjacent to the acute angle ,
 and the hypotenuse of the right triangle.

47. A
A
The hypotenuse is the longest side and is always
opposite the right angle.
The opposite and adjacent sides refer to another angle,
other than the 90o.
Right Triangle Trigonometry

48. S O H C A H T O A
The trigonometric functions are:
sine, cosine, tangent, cotangent, secant, and cosecant.
opp
adj
hyp
θ
sin  = cos  = tan  =
csc  = sec  = cot  =
opp
hyp
adj
hyp
hyp
adj
adj
opp
opp
adj
hyp
opp
Trigonometric Ratios

49. Finding an angle from a triangle
To find a missing angle from a right-angled triangle we
need to know two of the sides of the triangle.
We can then choose the appropriate ratio, sin, cos or tan
and use the calculator to identify the angle from the
decimal value of the ratio.
Find angle C
a) Identify/label the names of
the sides.
b) Choose the ratio that
contains BOTH of the
letters.
14 cm
6 cm
C
1.

50. C = cos-1 (0.4286)
C = 64.6o
14 cm
6 cm
C
1.
h
a
We have been given the
adjacent and hypotenuse so
we use COSINE:
Cos A = hypotenuse
adjacent
Cos A =
h
a
Cos C =
14
6
Cos C = 0.4286

51. Find angle x
2.
8 cm
3 cm
x
a
o
Given adj and opp
need to use tan:
Tan A = adjacent
opposite
x = tan-1 (2.6667)
x = 69.4o
Tan A =
a
o
Tan x =
3
8
Tan x = 2.6667

52. Cos 30 x 7 = k
6.1 cm = k
7 cm
k
30o
3. We have been given
the adj and hyp so we
use COSINE:
Cos A =
hypotenuse
adjacent
Cos A =
h
a
Cos 30 =
7
k
Finding a side from a triangle

53. Tan 50 x 4 = r
4.8 cm = r
4 cm
r
50o
4.
Tan A =
a
o
Tan 50 =
4
r
We have been given the opp
and adj so we use TAN:
Tan A =

54. 45°-45°-90° Triangle Theorem
• In a 45°-45°-90°
triangle, the
hypotenuse is √2
times as long as each
leg.
x
x
x√2
45°
45°
Hypotenuse = √2 * leg

55. 30°-60°-90° Triangle Theorem
• In a 30°-60°-90°
triangle, the
hypotenuse is twice
as long as the shorter
leg, and the longer
leg is √3 times as
long as the shorter
leg.
x√3
60°
30°
Hypotenuse = 2 ∙ shorter leg
Longer leg = √3 ∙ shorter leg
2x
x

56. Ex. 1: Finding the hypotenuse in a 45°-45°-
90° Triangle
• Find the value of x
• By the Triangle Sum
Theorem, the measure of
the third angle is 45°.
The triangle is a 45°-45°-
90° right triangle, so the
length x of the
hypotenuse is √2 times
the length of a leg.
3 3
x
45°

57. Ex. 1: Finding the hypotenuse in a 45°-45°-
90° Triangle
Hypotenuse = √2 ∙ leg
x = √2 ∙ 3
x = 3√2
3 3
x
45°
45°-45°-90° Triangle
Theorem
Substitute values
Simplify

58. Ex. 3: Finding side lengths in a 30°-60°-90°
Triangle
• Find the values of s
and t.
• Because the triangle
is a 30°-60°-90°
triangle, the
longer leg is √3
times the length s
of the shorter leg.
5
s
t
30°
60°

59. Ex. 3: Side lengths in a 30°-60°-90° Triangle
Statement:
Longer leg = √3 ∙ shorter leg
5 = √3 ∙ s
Reasons:
30°-60°-90° Triangle Theorem
5
√
3
√3
s√
3
=
5
√
3
s
=
5
√
3
s
=
√3
√
3 5√
3
3
s
=
Substitute values
Divide each side by √3
Simplify
Multiply numerator and
denominator by √3
Simplify
5
s
t
30°
60°

60. The length t of the hypotenuse is twice the length s of the shorter leg.
Statement:
Hypotenuse = 2 ∙ shorter leg
Reasons:
30°-60°-90° Triangle Theorem
t 2
∙
5√
3
3
= Substitute values
Simplify
5
s
t
30°
60°
t 10√
3
3
=