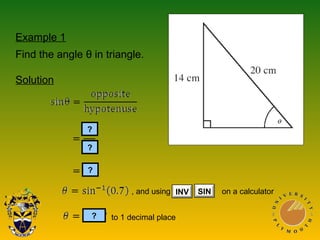
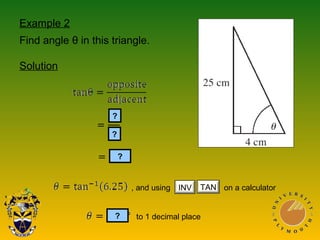
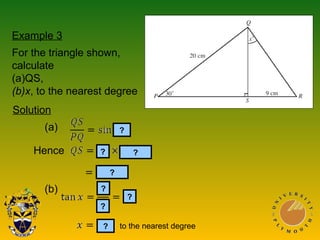
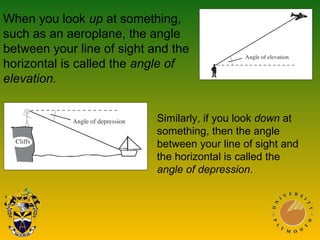
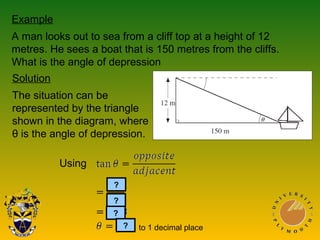
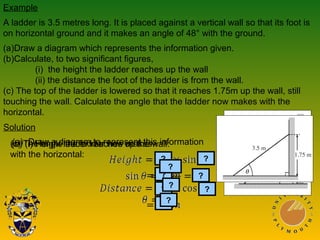
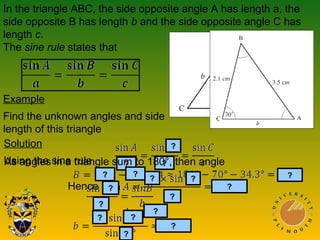
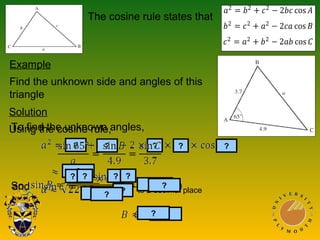
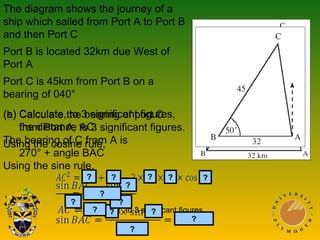
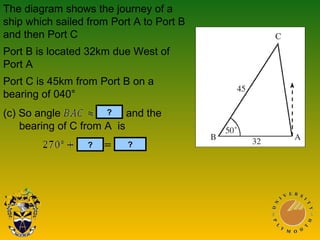
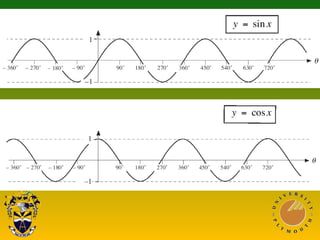
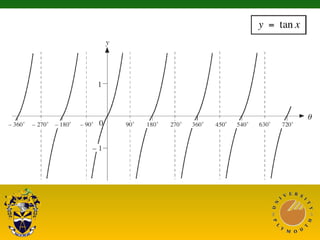
This document covers trigonometric concepts and problems involving right-angled triangles, bearings, and trigonometric functions. It includes 7 presentations on finding angles in right triangles using trig functions, problems using trigonometry including elevation and depression, the sine rule, cosine rule, problems with bearings, and trig functions. Examples are provided for each topic to demonstrate how to set up and solve various trigonometric problems.

1. Unit 35
Trigonometric Problems
Presentation 1 Finding Angles in Right Angled Triangles
Presentation 3 Problems using Trigonometry 2
Presentation 4 Sine Rule
Presentation 5 Cosine Rule
Presentation 6 Problems with Bearings
Presentation 7 Tangent Functions

2. Unit 35
35.1 Finding Angles in Right
Angled Triangles

3. Example 1
Find the angle θ in triangle.
Solution
?
?
?
? to 1 decimal place
, and using on a calculatorINV SIN

4. Example 2
Find angle θ in this triangle.
Solution
?
to 1 decimal place
?
?
?
, and using on a calculatorINV TAN

5. Example 3
For the triangle shown,
calculate
(a)QS,
(b)x, to the nearest degree
Solution
(a)
Hence
(b)
to the nearest degree
?
??
?
?
?
?
?

6. Unit 35
35.2 Problems Using
Trigonometry 1

7. When you look up at something,
such as an aeroplane, the angle
between your line of sight and the
horizontal is called the angle of
elevation.
Similarly, if you look down at
something, then the angle
between your line of sight and
the horizontal is called the
angle of depression.

8. Example
A man looks out to sea from a cliff top at a height of 12
metres. He sees a boat that is 150 metres from the cliffs.
What is the angle of depression
Solution
The situation can be
represented by the triangle
shown in the diagram, where
θ is the angle of depression.
Using
?
?
?
? to 1 decimal place

9. Unit 35
35.3 Problems using
Trigonometry 2

10. ?
Example
A ladder is 3.5 metres long. It is placed against a vertical wall so that its foot is
on horizontal ground and it makes an angle of 48° with the ground.
(a)Draw a diagram which represents the information given.
(b)Calculate, to two significant figures,
(i) the height the ladder reaches up the wall
(ii) the distance the foot of the ladder is from the wall.
(c) The top of the ladder is lowered so that it reaches 1.75m up the wall, still
touching the wall. Calculate the angle that the ladder now makes with the
horizontal.
Solution
(a) Draw a diagram to represent this information
?
?(b) (i) Height ladder reaches up the wall:
?
?
??
?
(c) The angle the ladder now makes
with the horizontal:
?
?
?
?

11. Unit 35
35.4 Sine Rule

12. In the triangle ABC, the side opposite angle A has length a, the
side opposite B has length b and the side opposite angle C has
length c.
The sine rule states that
Example
Find the unknown angles and side
length of this triangle
Solution
Using the sine rule
Hence
?
?
??
?
?
??
?
As angles in a triangle sum to 180°, then angle
?
???
?
?
?
?

13. Unit 35
35.5 Cosine Rule

14. The cosine rule states that
Example
Find the unknown side and angles of this
triangle
Solution
Using the cosine rule,
to 2 decimal place
??
?
?
? ??? ?
To find the unknown angles,
?
?
??
Soand ?
?
??

15. Unit 35
35.6 Problems with Bearings

16. The diagram shows the journey of a
ship which sailed from Port A to Port B
and then Port C
Port B is located 32km due West of
Port A
Port C is 45km from Port B on a
bearing of 040°
(a) Calculate, to 3 significant figures,
the distance AC.
Using the cosine rule,
to 3 significant figures?
?
?
?
?
?
?
? ? ??
(b) Calculate the bearing of port C
from Port A, to 3 significant figures.
The bearing of C from A is
270° + angle BAC
Using the sine rule,
?
?
?

17. The diagram shows the journey of a
ship which sailed from Port A to Port B
and then Port C
Port B is located 32km due West of
Port A
Port C is 45km from Port B on a
bearing of 040°
(c) So angle and the
bearing of C from A is
?
? ?

18. Unit 35
35.7 Trig Functions

19. Note that for any angle θ
Also, there are some special values for some angles, as shown
below