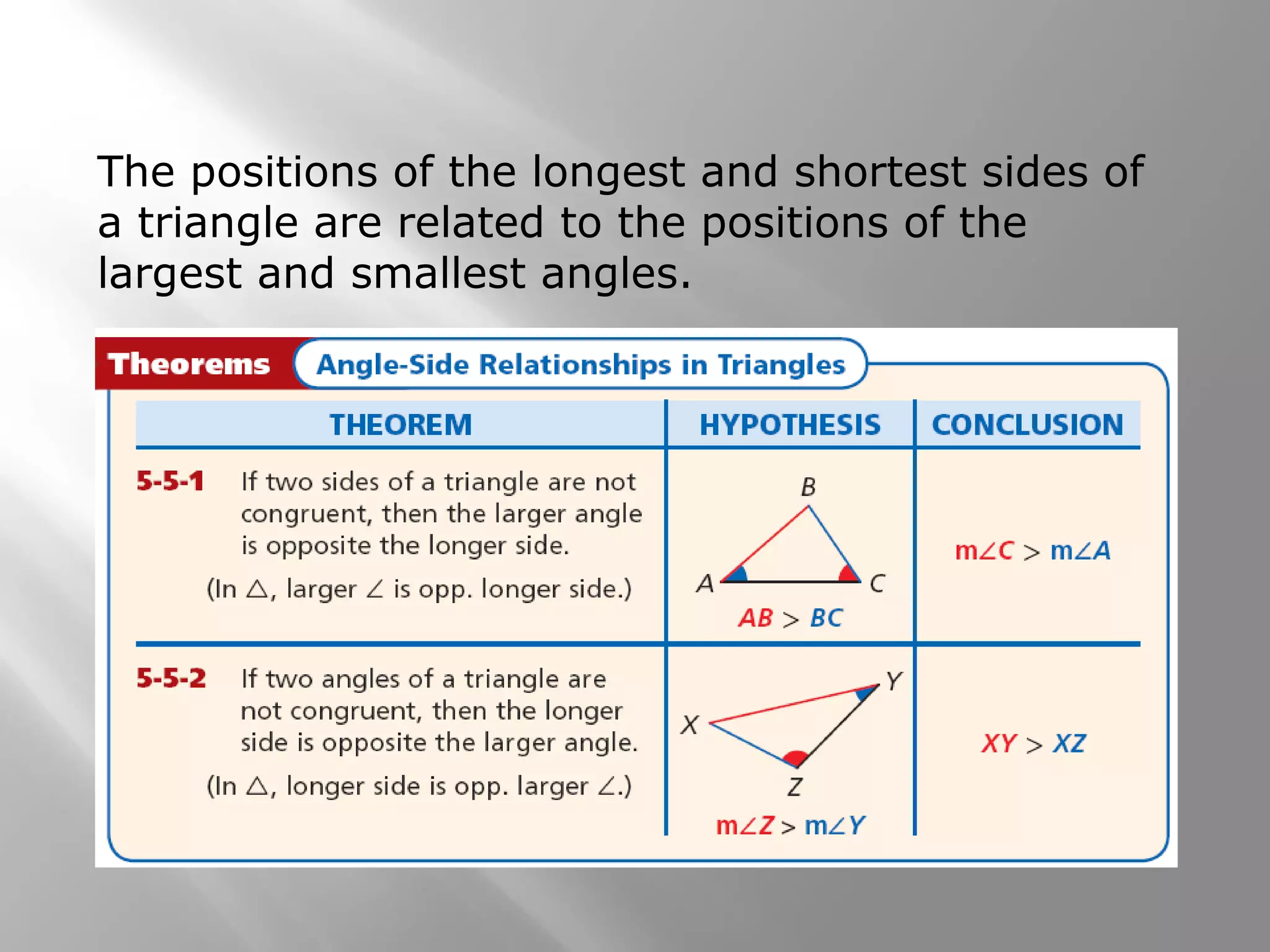
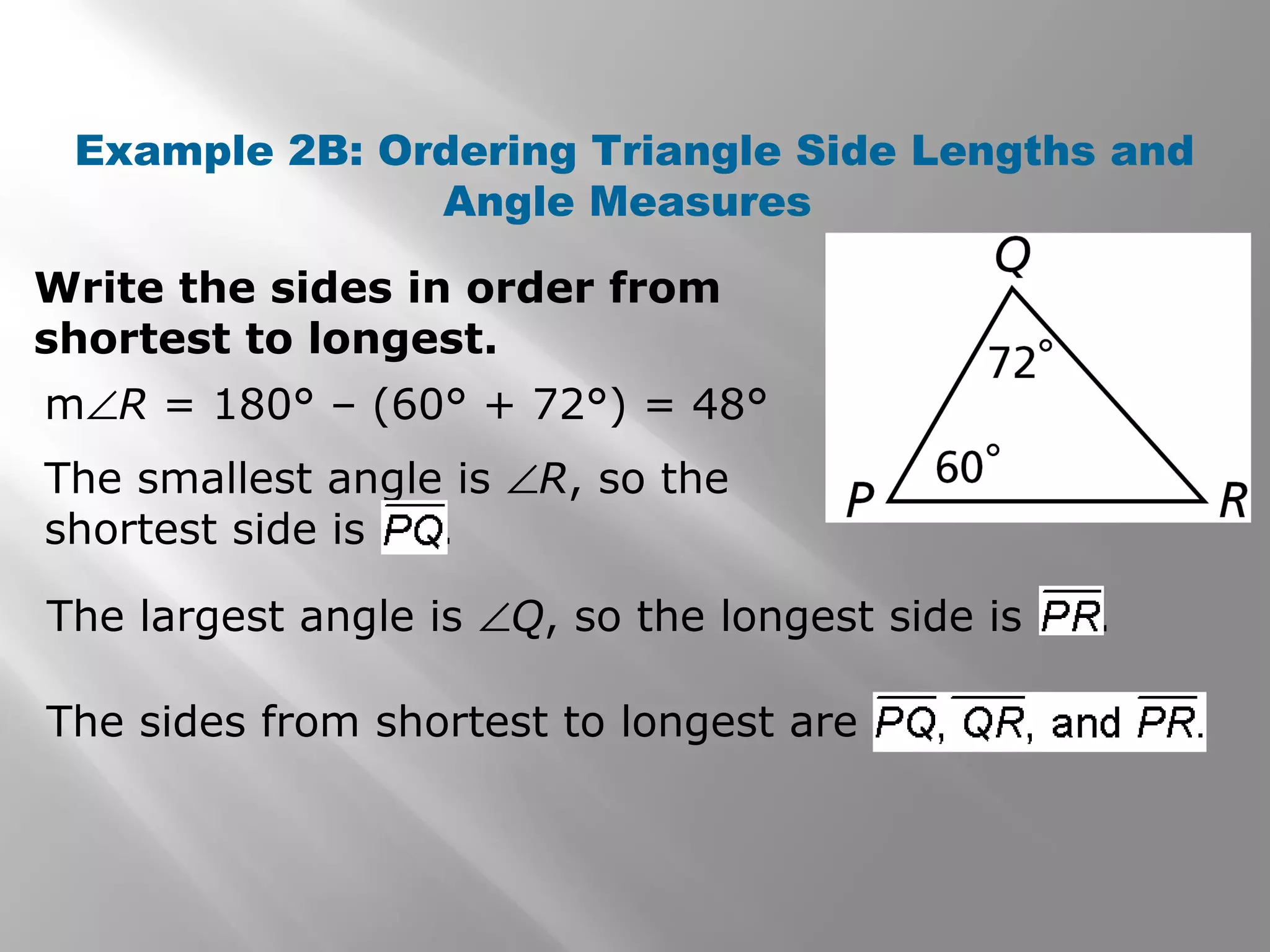
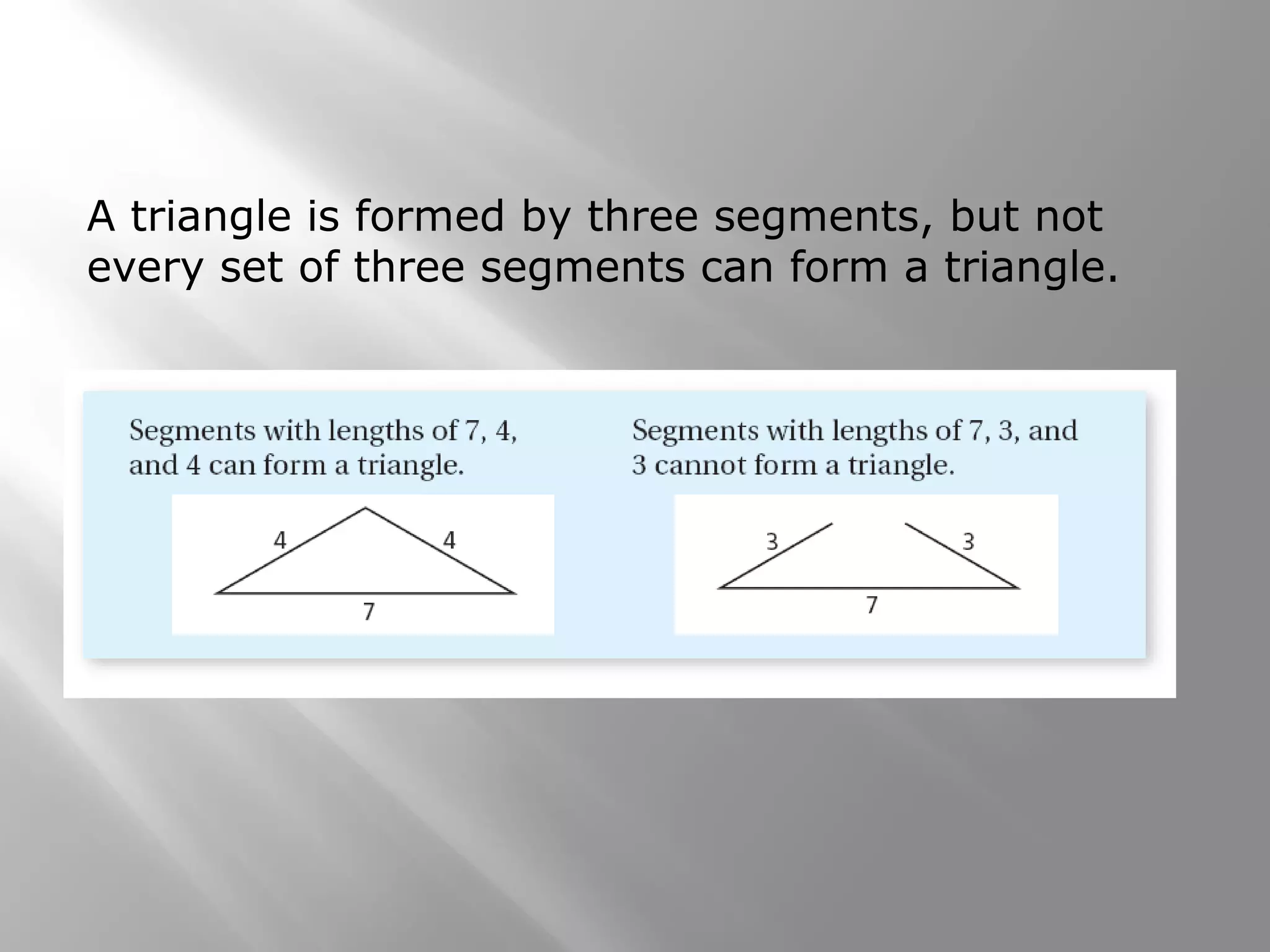
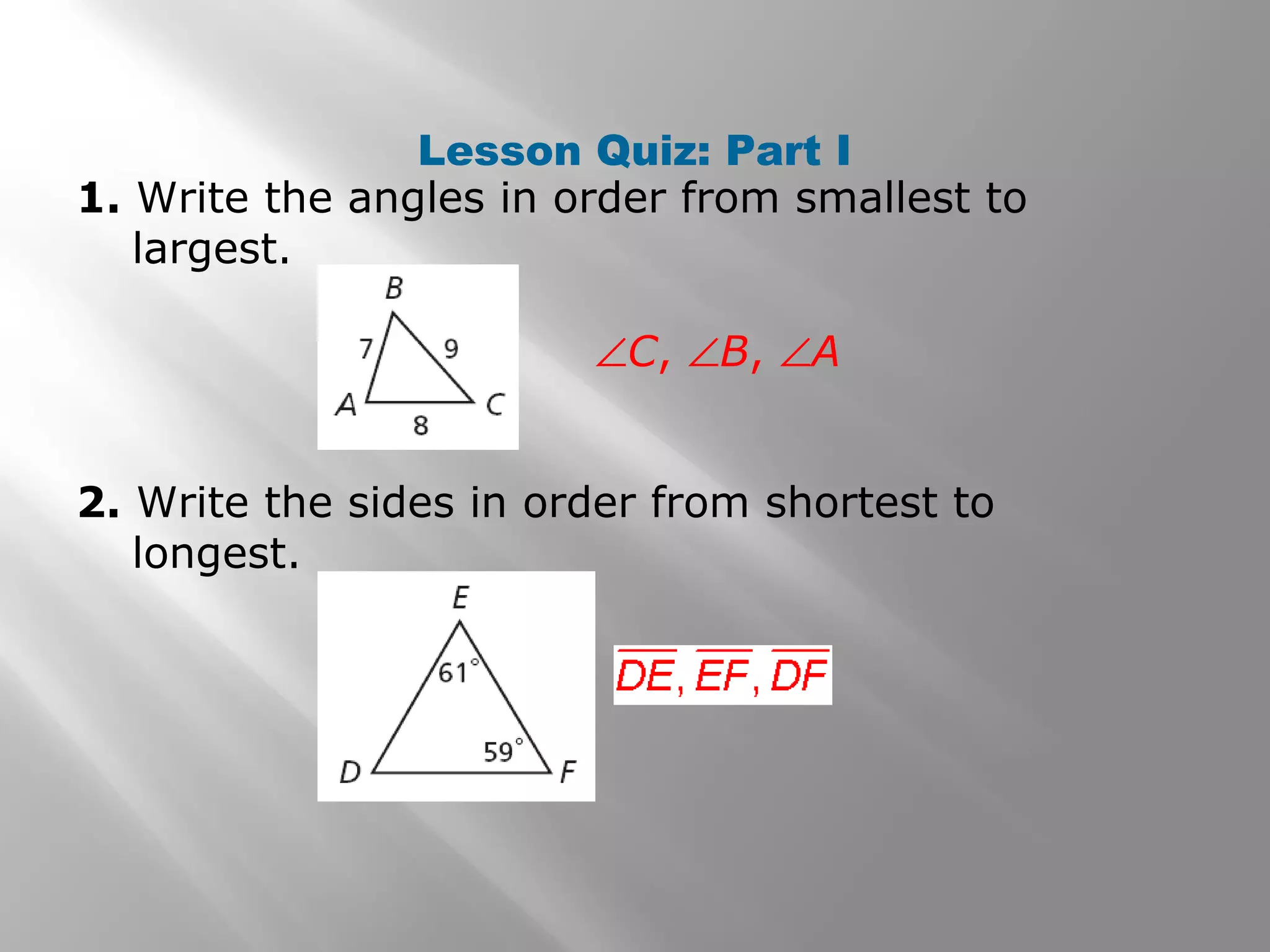
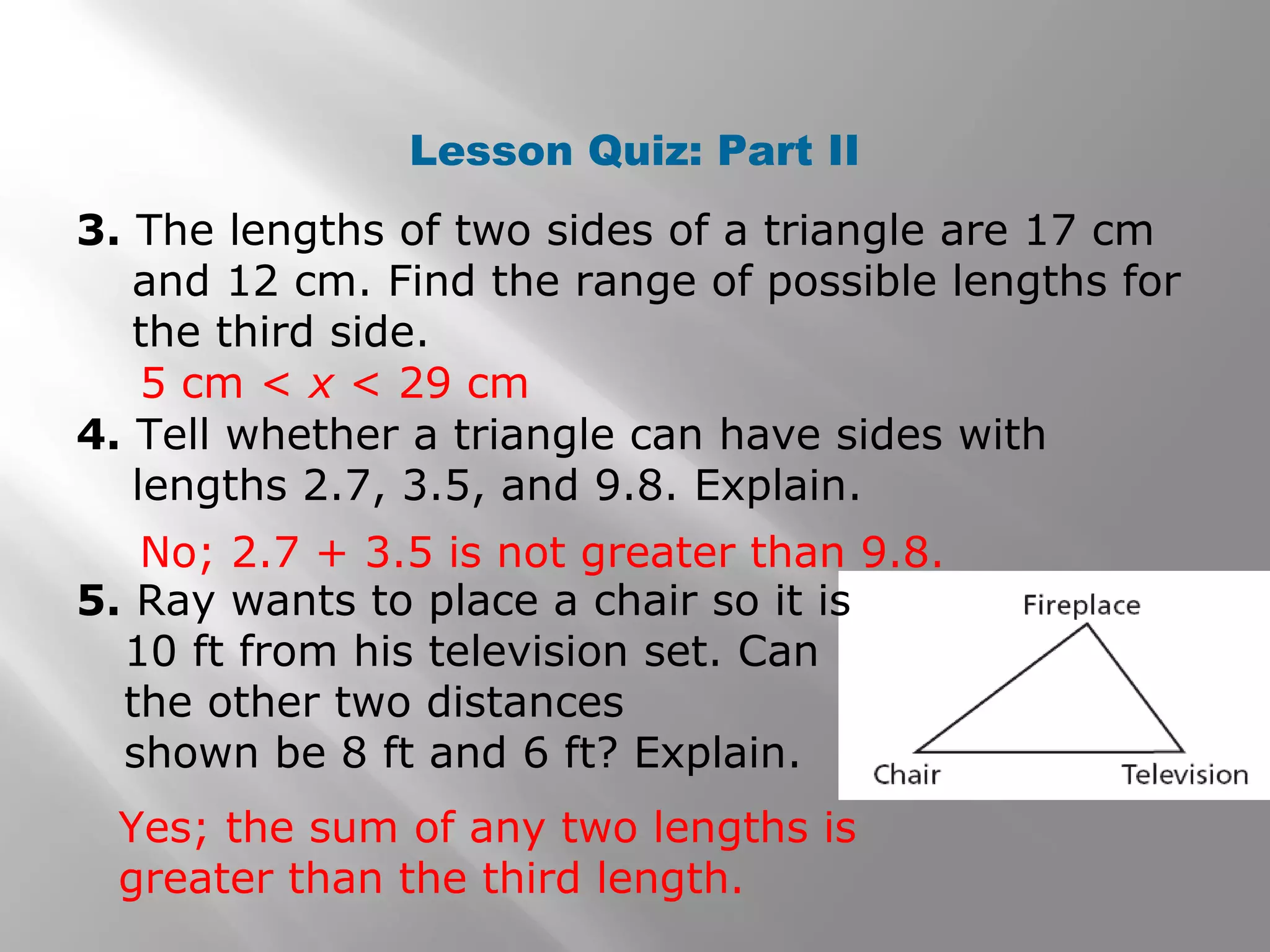
This document provides examples and explanations of indirect proofs. It begins with examples of writing indirect proofs to show that a triangle cannot have two right angles or that a number is greater than 0. It then discusses using inequalities in indirect proofs involving triangles. Examples demonstrate ordering triangle sides and angles, applying the triangle inequality theorem to determine if a triangle can exist with given side lengths, and using indirect proofs to find possible side lengths. The document concludes with practice problems applying these concepts.

1. UNIT 5.5 INDIRECT PROOFUNIT 5.5 INDIRECT PROOF

2. Warm Up
1. Write a conditional from the sentence “An
isosceles triangle has two congruent sides.”
2. Write the contrapositive of the conditional “If it
is Tuesday, then John has a piano lesson.”
3. Show that the conjecture “If x > 6, then 2x >
14” is false by finding a counterexample.
If a ∆ is isosc., then it has 2 ≅ sides.
If John does not have a piano lesson, then it is
not Tuesday.
x = 7

3. Write indirect proofs.
Apply inequalities in one triangle.
Objectives

4. indirect proof
Vocabulary

5. So far you have written proofs using direct reasoning.
You began with a true hypothesis and built a logical
argument to show that a conclusion was true. In an
indirect proof, you begin by assuming that the
conclusion is false. Then you show that this
assumption leads to a contradiction. This type of
proof is also called a proof by contradiction.

7. When writing an indirect proof, look for a
contradiction of one of the following: the given
information, a definition, a postulate, or a
theorem.
Helpful Hint

8. Example 1: Writing an Indirect Proof
Step 1 Identify the conjecture to be proven.
Given: a > 0
Step 2 Assume the opposite of the conclusion.
Write an indirect proof that if a > 0, then
Prove:
Assume

9. Example 1 Continued
Step 3 Use direct reasoning to lead to a contradiction.
However, 1 > 0.
1 ≤ 0
Given, opposite of conclusion
Zero Prop. of Mult. Prop. of Inequality
Simplify.

10. Step 4 Conclude that the original conjecture is true.
Example 1 Continued
The assumption that is false.
Therefore

11. Check It Out! Example 1
Write an indirect proof that a triangle cannot
have two right angles.
Step 1 Identify the conjecture to be proven.
Given: A triangle’s interior angles add up to 180°.
Prove: A triangle cannot have two right angles.
Step 2 Assume the opposite of the conclusion.
An angle has two right angles.

12. Check It Out! Example 1 Continued
Step 3 Use direct reasoning to lead to a contradiction.
However, by the Protractor Postulate, a triangle
cannot have an angle with a measure of 0°.
m∠1 + m∠2 + m∠3 = 180°
90° + 90° + m∠3 = 180°
180° + m∠3 = 180°
m∠3 = 0°

13. Step 4 Conclude that the original conjecture is true.
The assumption that a triangle can have
two right angles is false.
Therefore a triangle cannot have two right
angles.
Check It Out! Example 1 Continued

14. The positions of the longest and shortest sides of
a triangle are related to the positions of the
largest and smallest angles.

15. Example 2A: Ordering Triangle Side Lengths and
Angle Measures
Write the angles in order from
smallest to largest.
The angles from smallest to largest are ∠F, ∠H and ∠G.
The shortest side is , so the
smallest angle is ∠F.
The longest side is , so the largest angle is ∠G.

16. Example 2B: Ordering Triangle Side Lengths and
Angle Measures
Write the sides in order from
shortest to longest.
m∠R = 180° – (60° + 72°) = 48°
The smallest angle is ∠R, so the
shortest side is .
The largest angle is ∠Q, so the longest side is .
The sides from shortest to longest are

17. Check It Out! Example 2a
Write the angles in order from
smallest to largest.
The angles from smallest to largest are ∠B, ∠A, and ∠C.
The shortest side is , so the
smallest angle is ∠B.
The longest side is , so the largest angle is ∠C.

18. Check It Out! Example 2b
Write the sides in order from
shortest to longest.
m∠E = 180° – (90° + 22°) = 68°
The smallest angle is ∠D, so the shortest side is .
The largest angle is ∠F, so the longest side is .
The sides from shortest to longest are

19. A triangle is formed by three segments, but not
every set of three segments can form a triangle.

20. A certain relationship must exist among the lengths
of three segments in order for them to form a
triangle.

21. Example 3A: Applying the Triangle Inequality
Theorem
Tell whether a triangle can have sides with the
given lengths. Explain.
7, 10, 19
No—by the Triangle Inequality Theorem, a triangle
cannot have these side lengths.

22. Example 3B: Applying the Triangle Inequality
Theorem
Tell whether a triangle can have sides with the
given lengths. Explain.
2.3, 3.1, 4.6
Yes—the sum of each pair of lengths is greater
than the third length.
 

23. Example 3C: Applying the Triangle Inequality
Theorem
Tell whether a triangle can have sides with the
given lengths. Explain.
n + 6, n2
– 1, 3n, when n = 4.
Step 1 Evaluate each expression when n = 4.
n + 6
4 + 6
10
n2
– 1
(4)2
– 1
15
3n
3(4)
12

24. Example 3C Continued
Step 2 Compare the lengths.
Yes—the sum of each pair of lengths is greater
than the third length.
  

25. Check It Out! Example 3a
Tell whether a triangle can have sides with the
given lengths. Explain.
8, 13, 21
No—by the Triangle Inequality Theorem, a triangle
cannot have these side lengths.

26. Check It Out! Example 3b
Tell whether a triangle can have sides with the
given lengths. Explain.
6.2, 7, 9
Yes—the sum of each pair of lengths is greater
than the third side.
  

27. Check It Out! Example 3c
Tell whether a triangle can have sides with the
given lengths. Explain.
t – 2, 4t, t2
+ 1, when t = 4
Step 1 Evaluate each expression when t = 4.
t – 2
4 – 2
2
t2
+ 1
(4)2
+ 1
17
4t
4(4)
16

28. Check It Out! Example 3c Continued
Step 2 Compare the lengths.
Yes—the sum of each pair of lengths is greater
than the third length.
  

29. Example 4: Finding Side Lengths
The lengths of two sides of a triangle are 8
inches and 13 inches. Find the range of
possible lengths for the third side.
Let x represent the length of the third side. Then
apply the Triangle Inequality Theorem.
Combine the inequalities. So 5 < x < 21. The length
of the third side is greater than 5 inches and less
than 21 inches.
x + 8 > 13
x > 5
x + 13 > 8
x > –5
8 + 13 > x
21 > x

30. Check It Out! Example 4
The lengths of two sides of a triangle are 22
inches and 17 inches. Find the range of possible
lengths for the third side.
Let x represent the length of the third side. Then
apply the Triangle Inequality Theorem.
Combine the inequalities. So 5 < x < 39. The length
of the third side is greater than 5 inches and less
than 39 inches.
x + 22 > 17
x > –5
x + 17 > 22
x > 5
22 + 17 > x
39 > x

31. Example 5: Travel Application
The figure shows the
approximate distances
between cities in California.
What is the range of distances
from San Francisco to Oakland?
Let x be the distance from San Francisco to Oakland.
x + 46 > 51
x > 5
x + 51 > 46
x > –5
46 + 51 > x
97 > x
5 < x < 97 Combine the inequalities.
Δ Inequal. Thm.
Subtr. Prop. of
Inequal.
The distance from San Francisco to Oakland is
greater than 5 miles and less than 97 miles.

32. Check It Out! Example 5
The distance from San Marcos to Johnson City is
50 miles, and the distance from Seguin to San
Marcos is 22 miles. What is the range of
distances from Seguin to Johnson City?
Let x be the distance from Seguin to Johnson City.
x + 22 > 50
x > 28
x + 50 > 22
x > –28
22 + 50 > x
72 > x
28 < x < 72 Combine the inequalities.
Δ Inequal. Thm.
Subtr. Prop. of
Inequal.
The distance from Seguin to Johnson City is greater
than 28 miles and less than 72 miles.

33. Lesson Quiz: Part I
1. Write the angles in order from smallest to
largest.
2. Write the sides in order from shortest to
longest.
∠C, ∠B, ∠A

34. Lesson Quiz: Part II
3. The lengths of two sides of a triangle are 17 cm
and 12 cm. Find the range of possible lengths for
the third side.
4. Tell whether a triangle can have sides with
lengths 2.7, 3.5, and 9.8. Explain.
No; 2.7 + 3.5 is not greater than 9.8.
5 cm < x < 29 cm
5. Ray wants to place a chair so it is
10 ft from his television set. Can
the other two distances
shown be 8 ft and 6 ft? Explain.
Yes; the sum of any two lengths is
greater than the third length.

35. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.