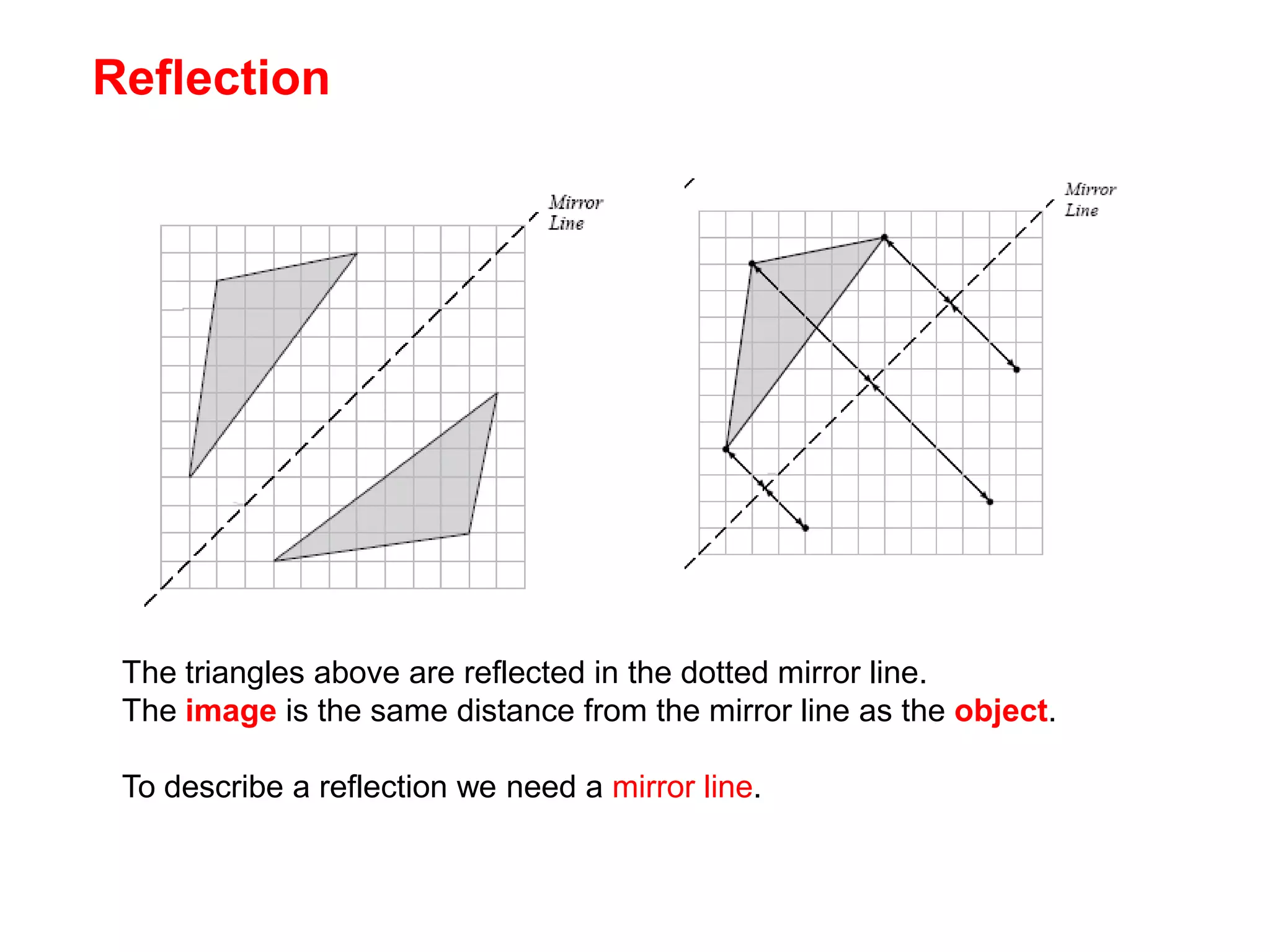
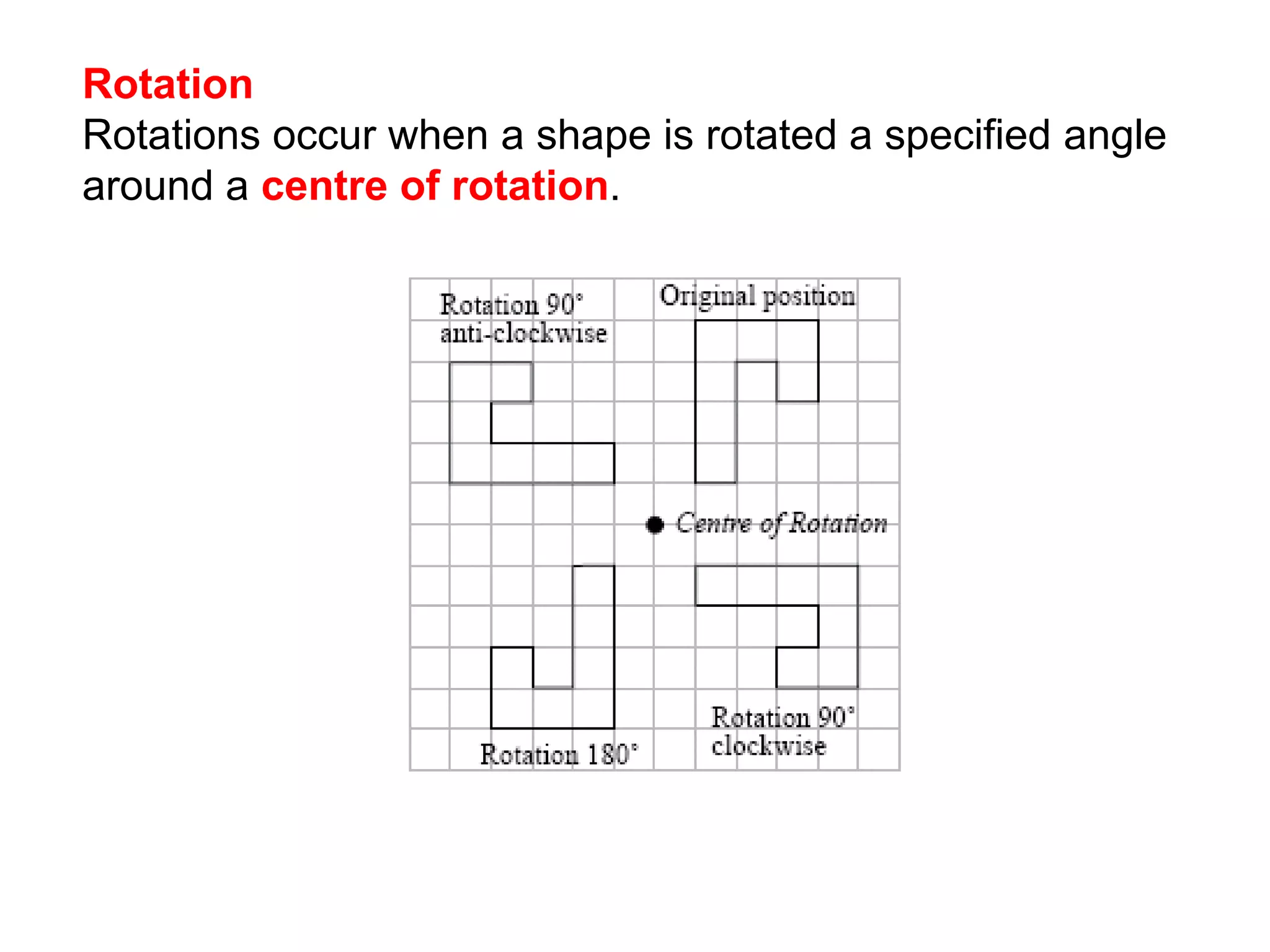
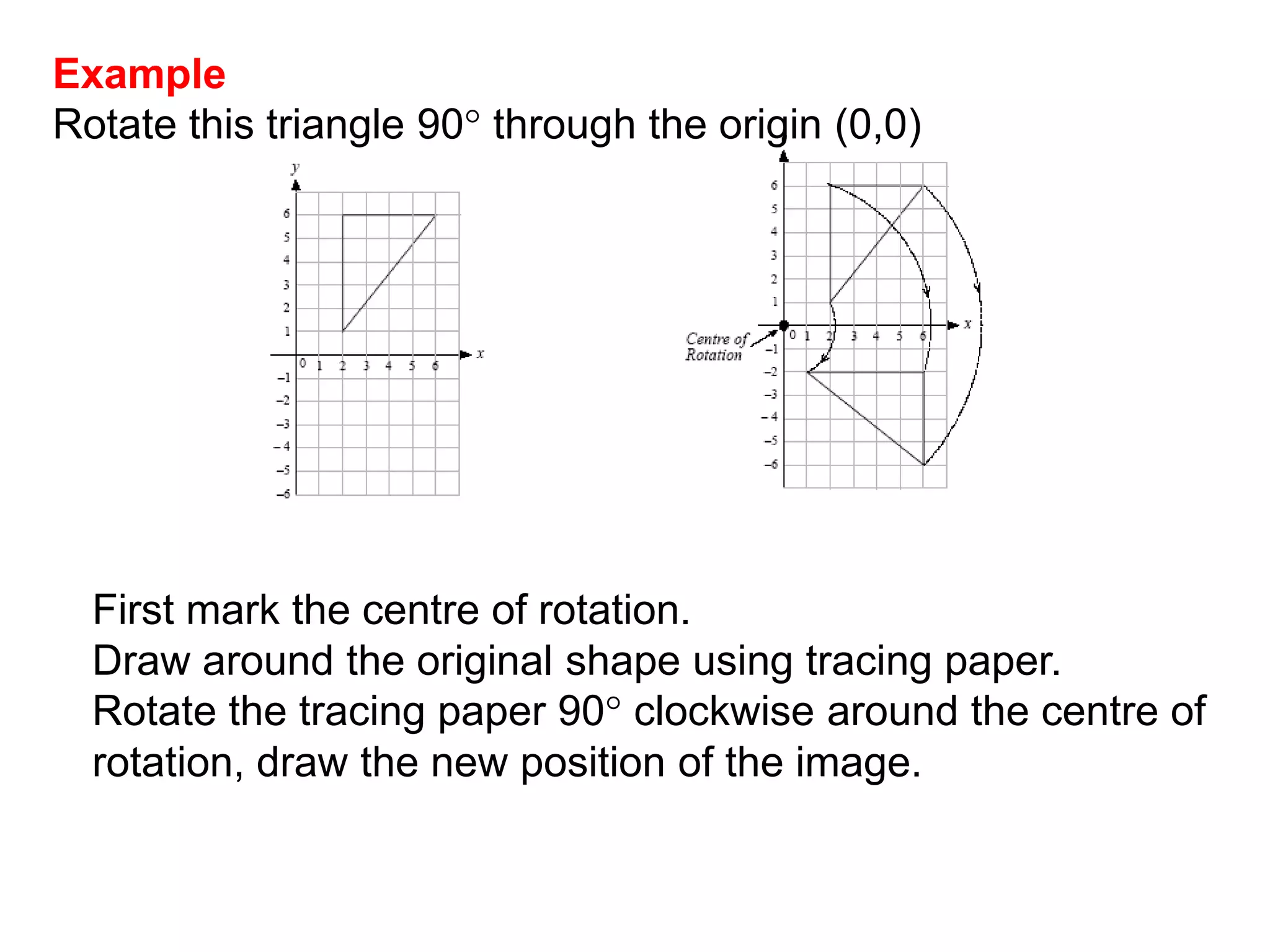
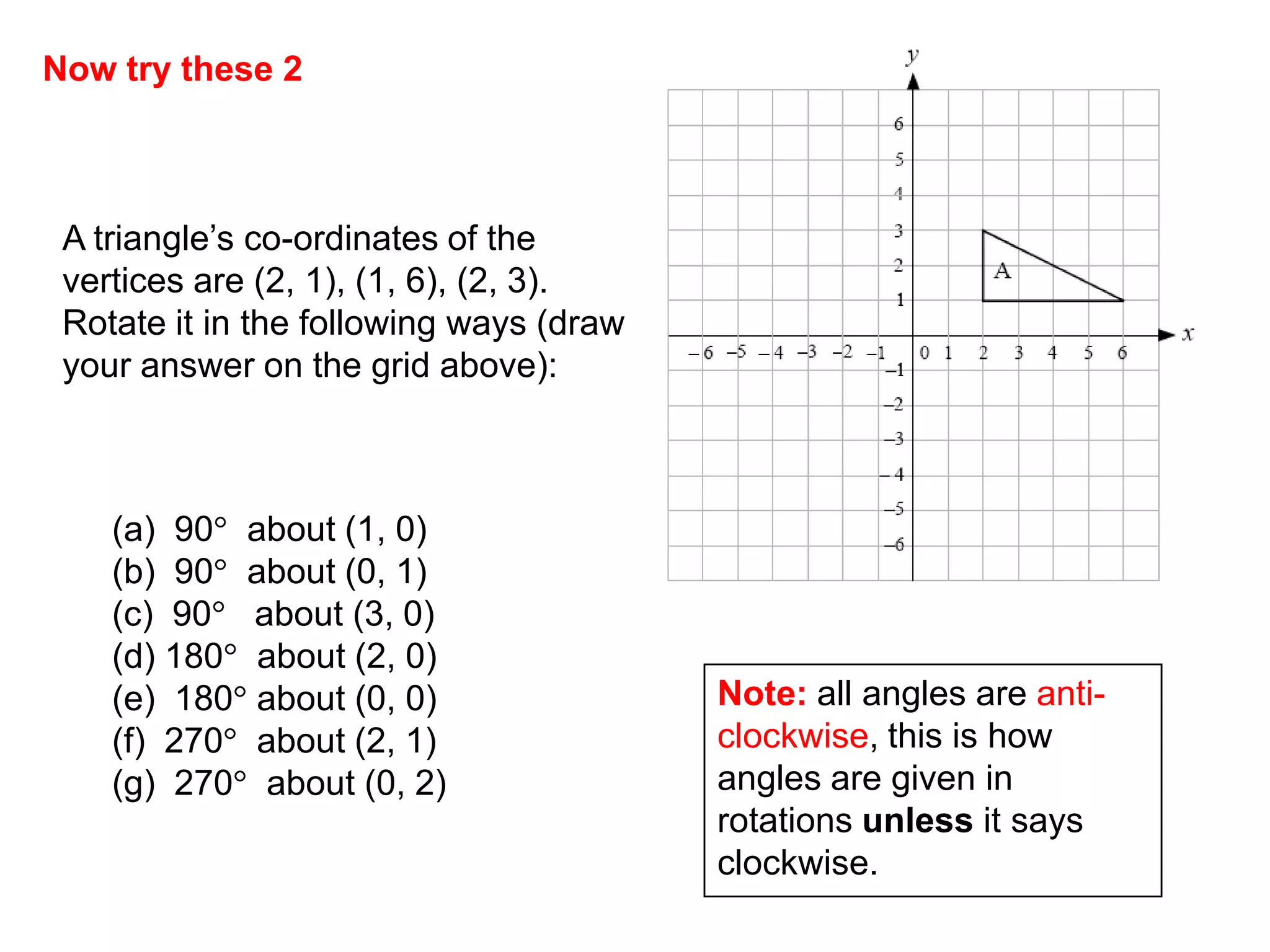
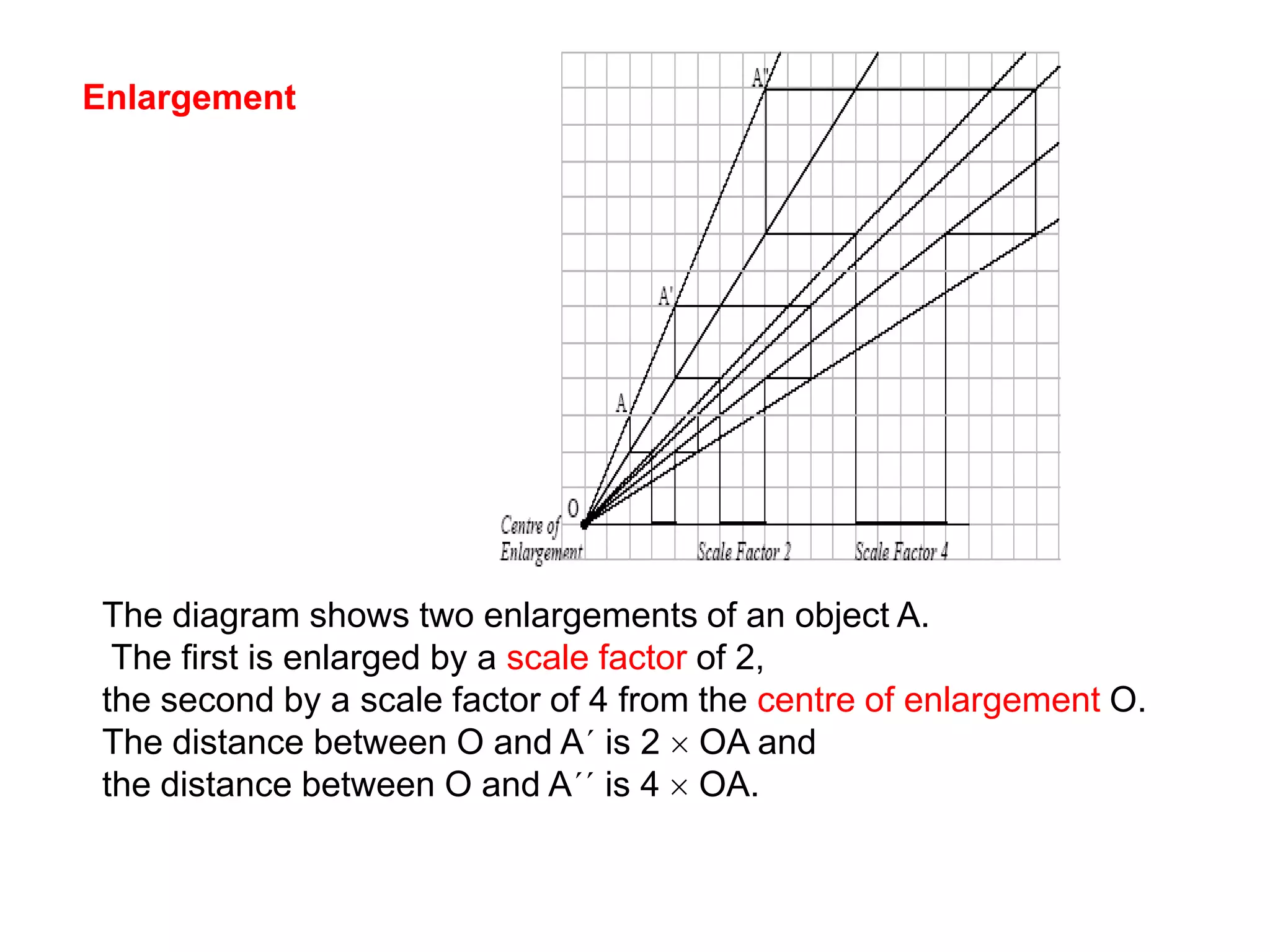
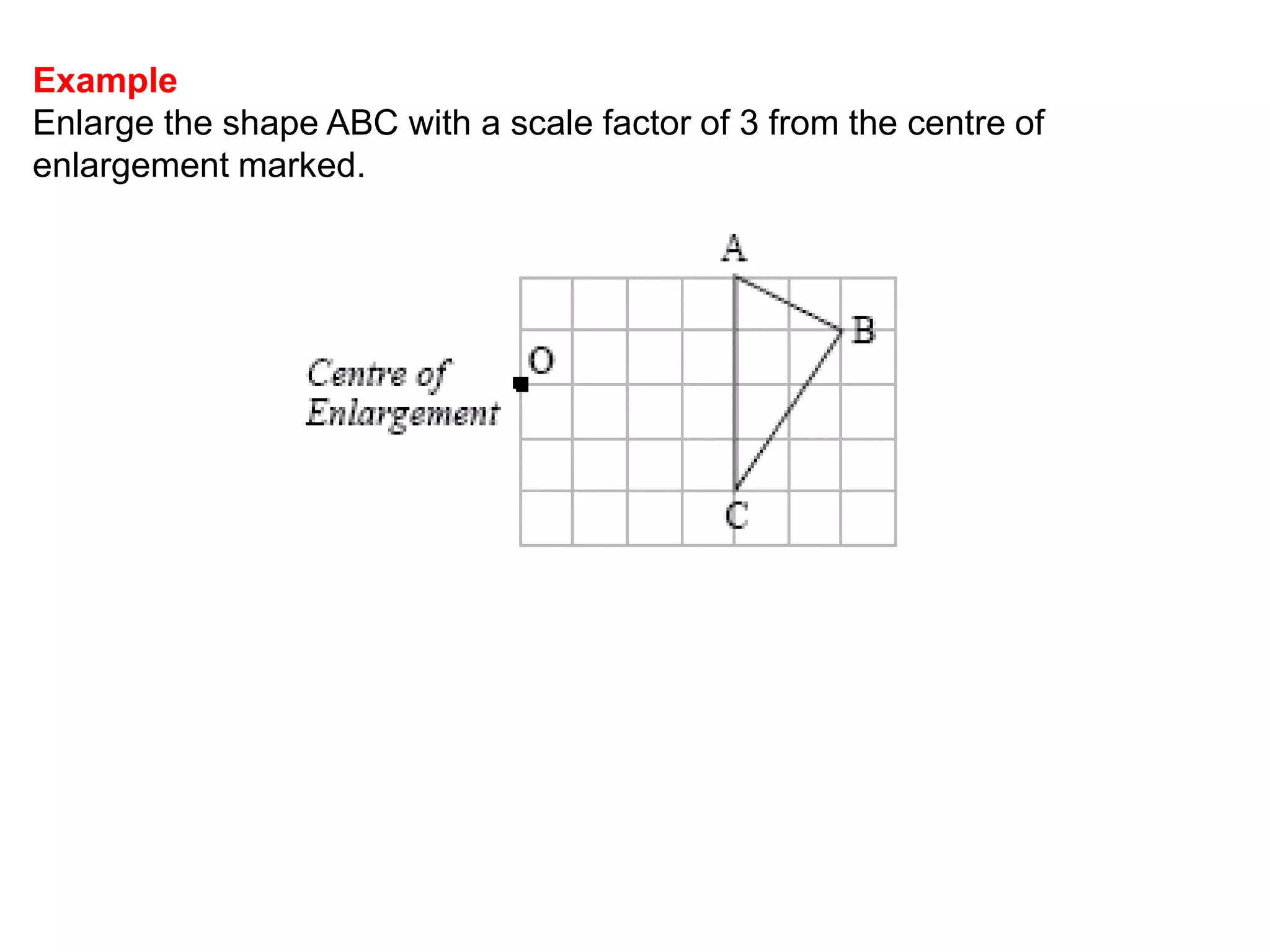
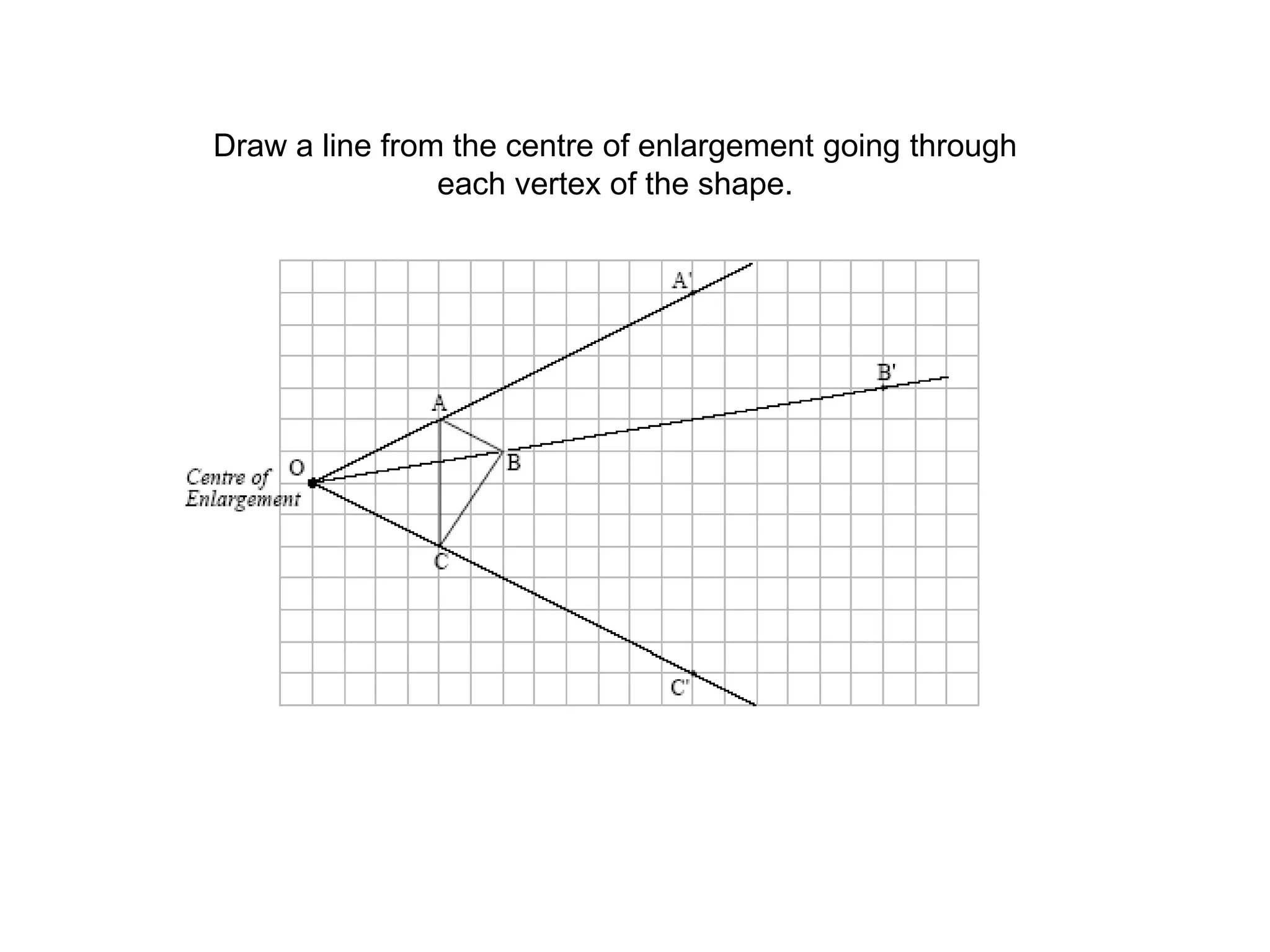
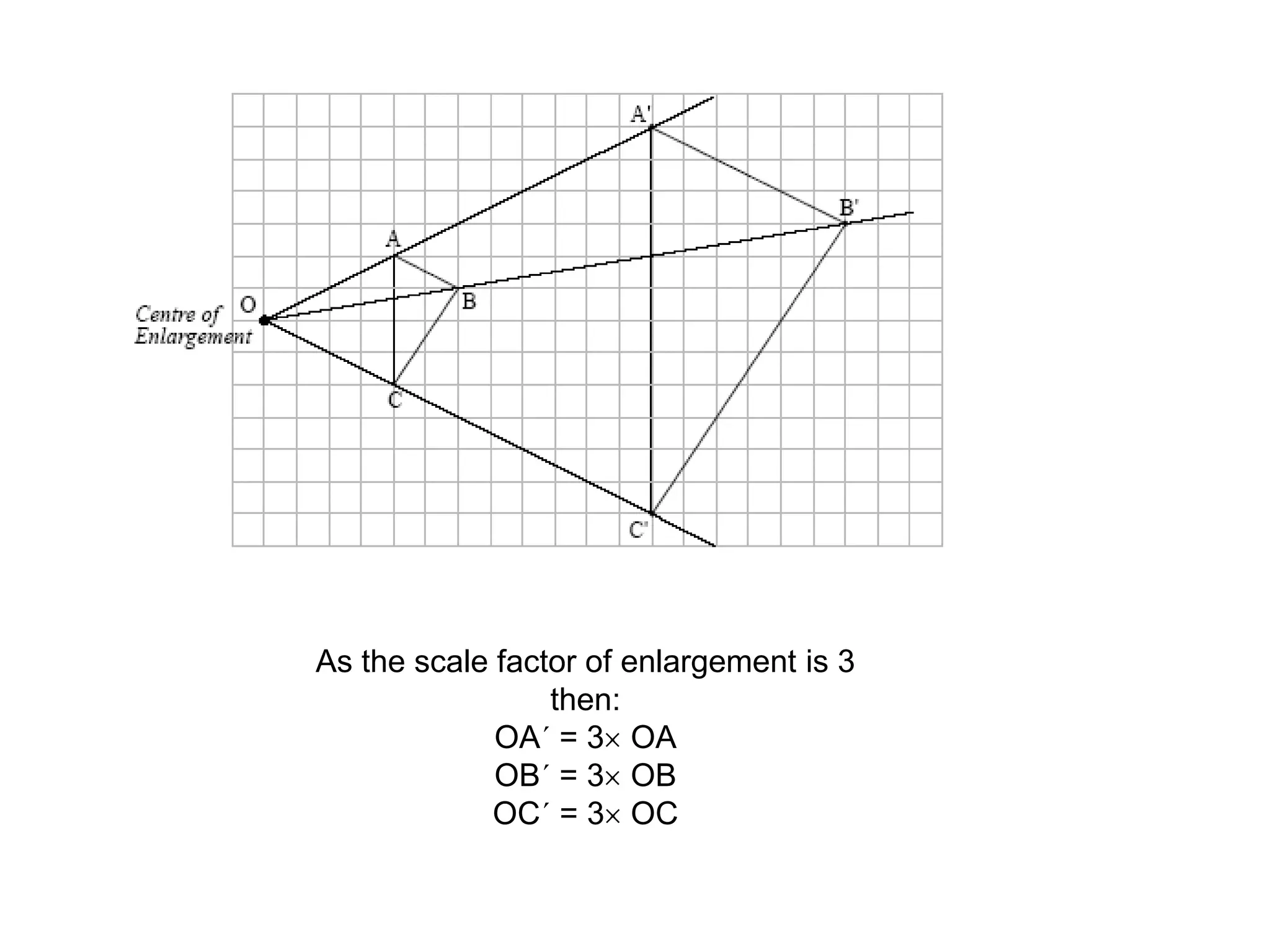
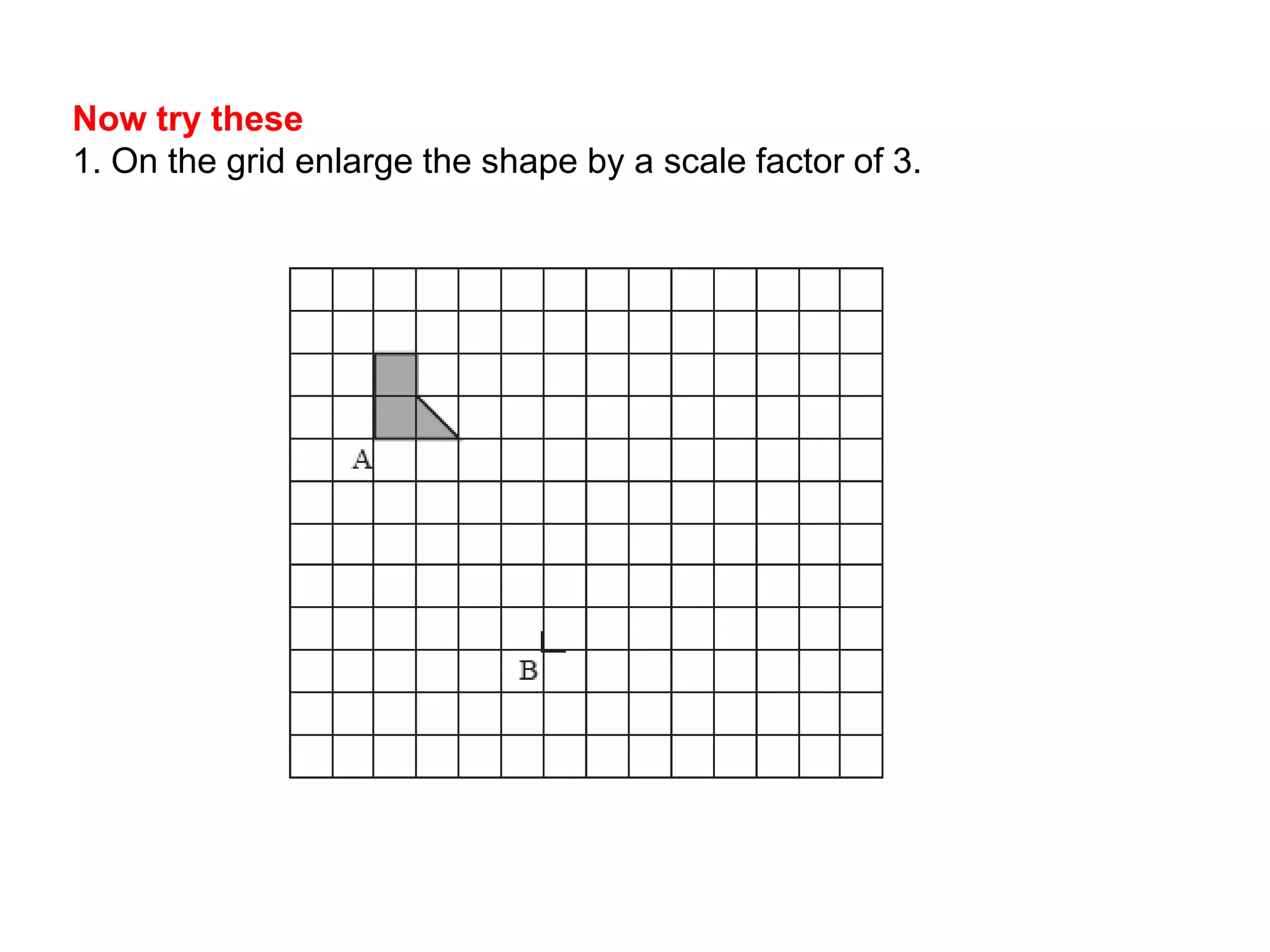
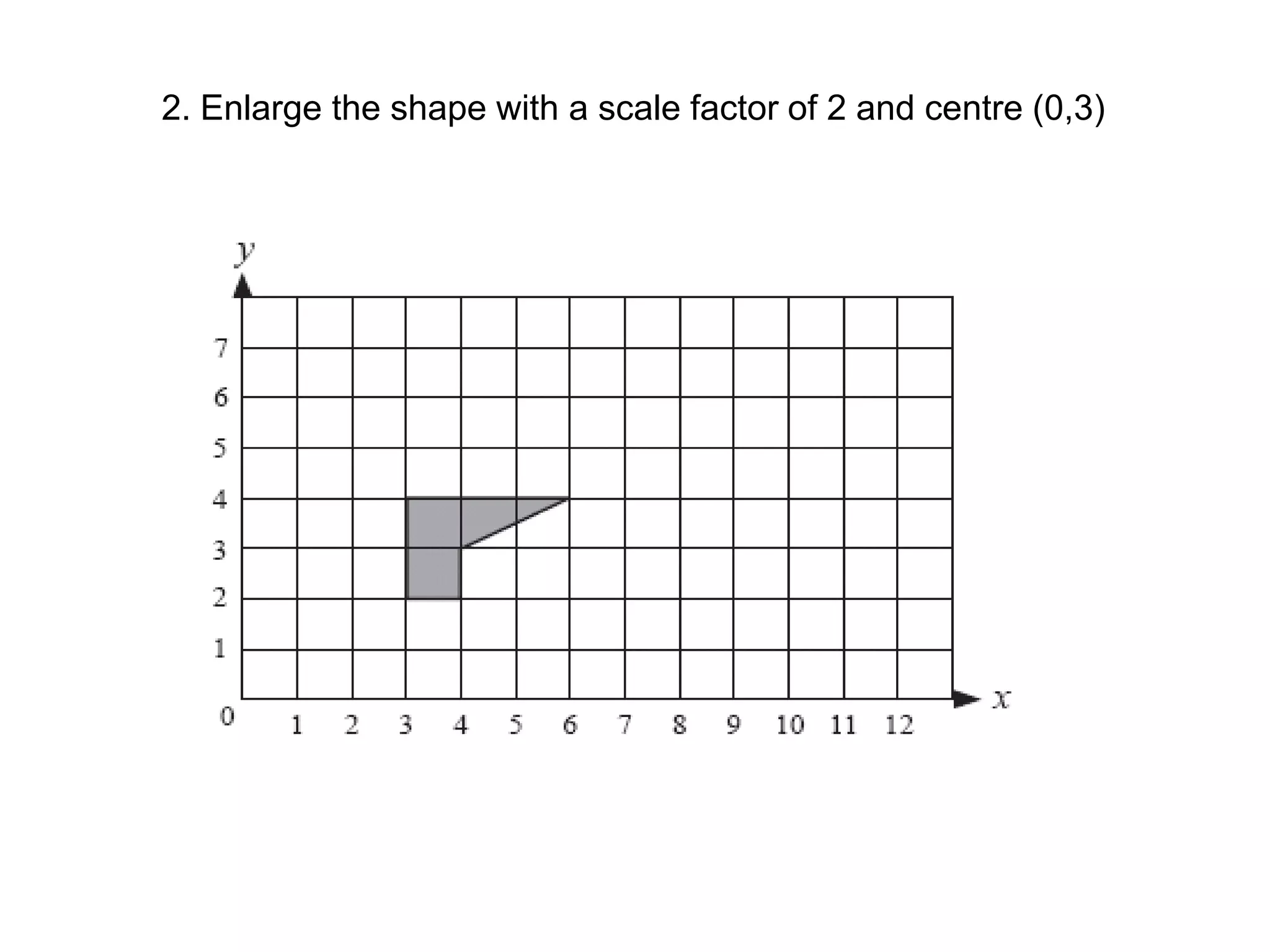
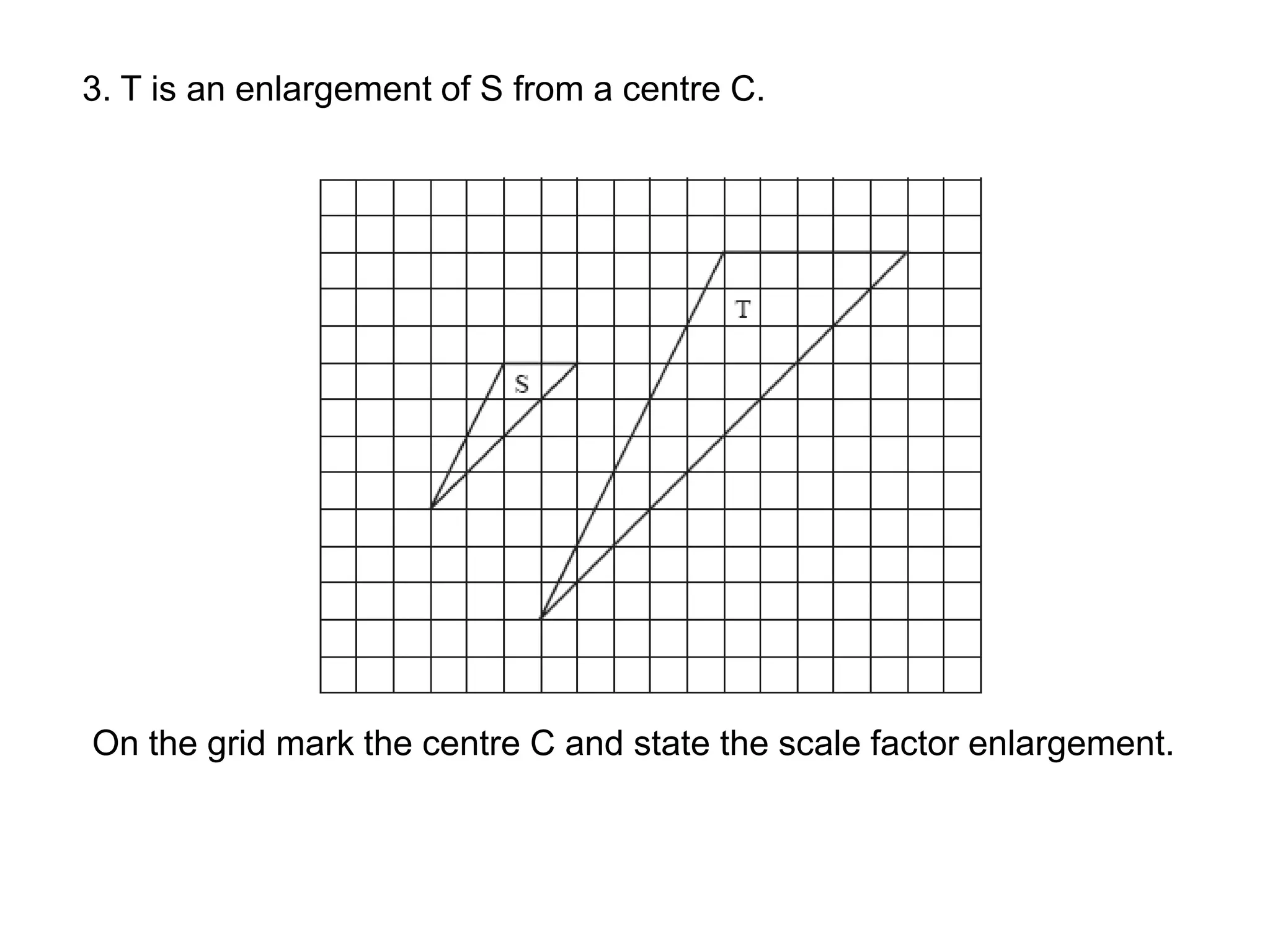
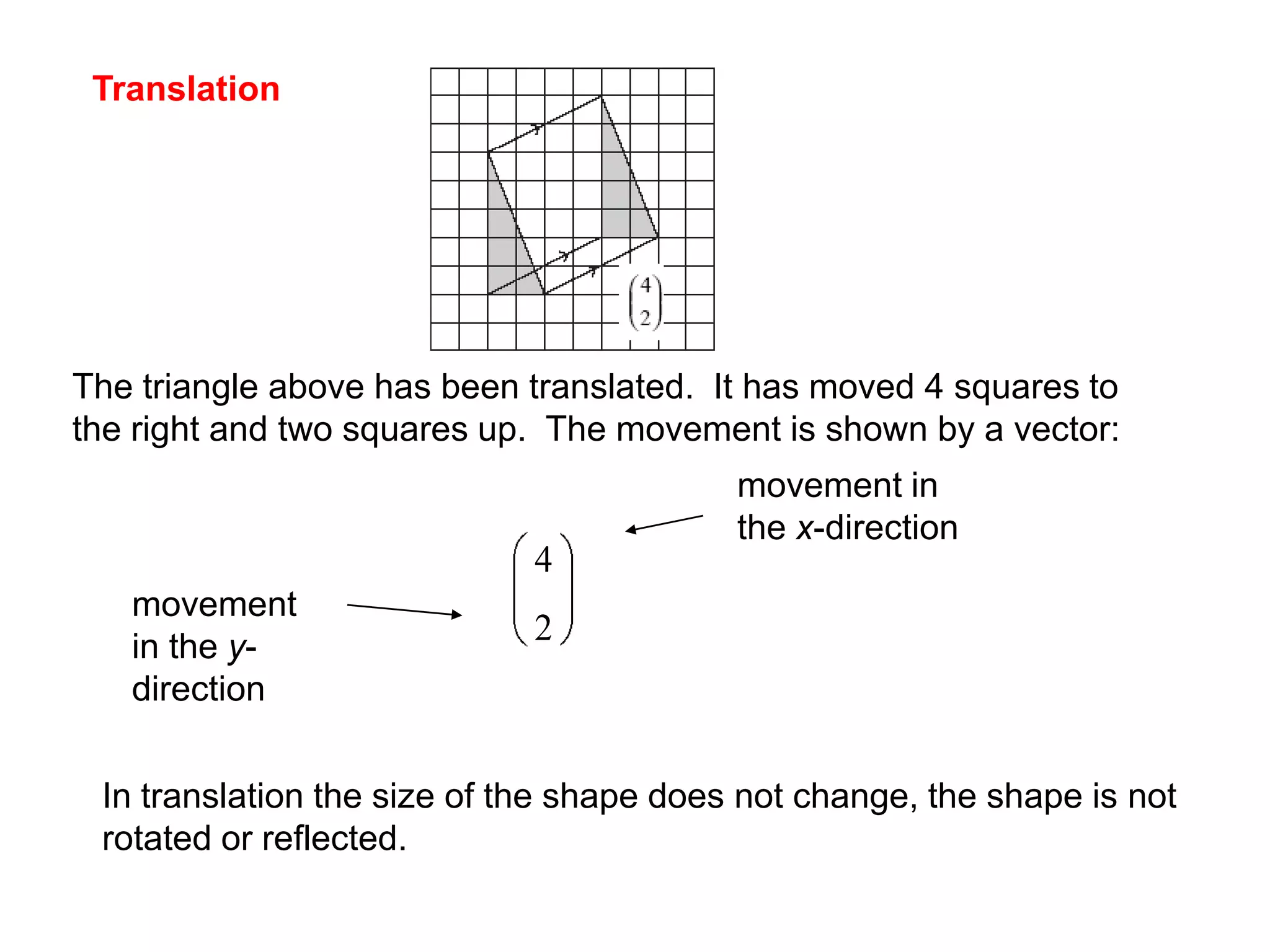
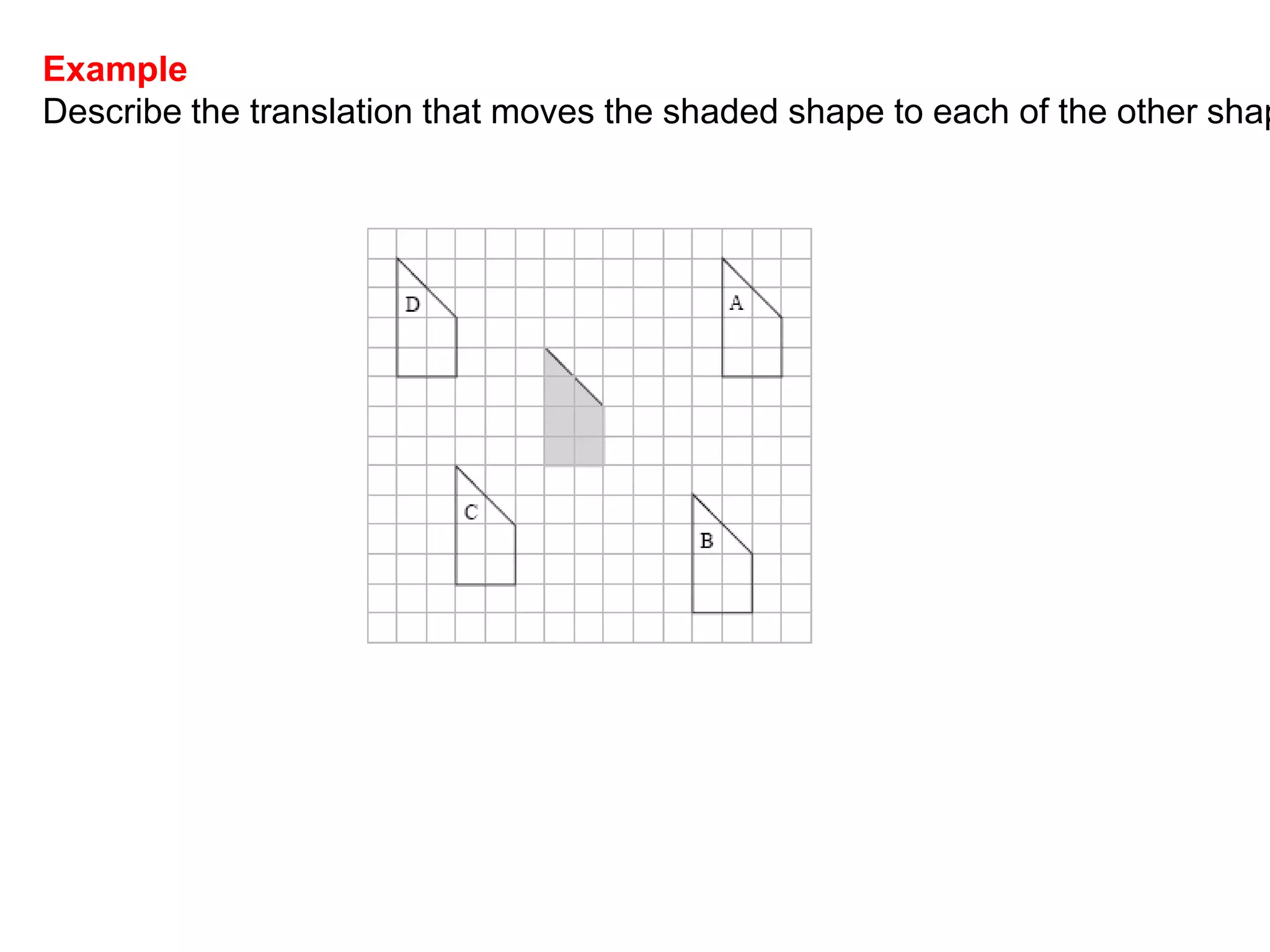
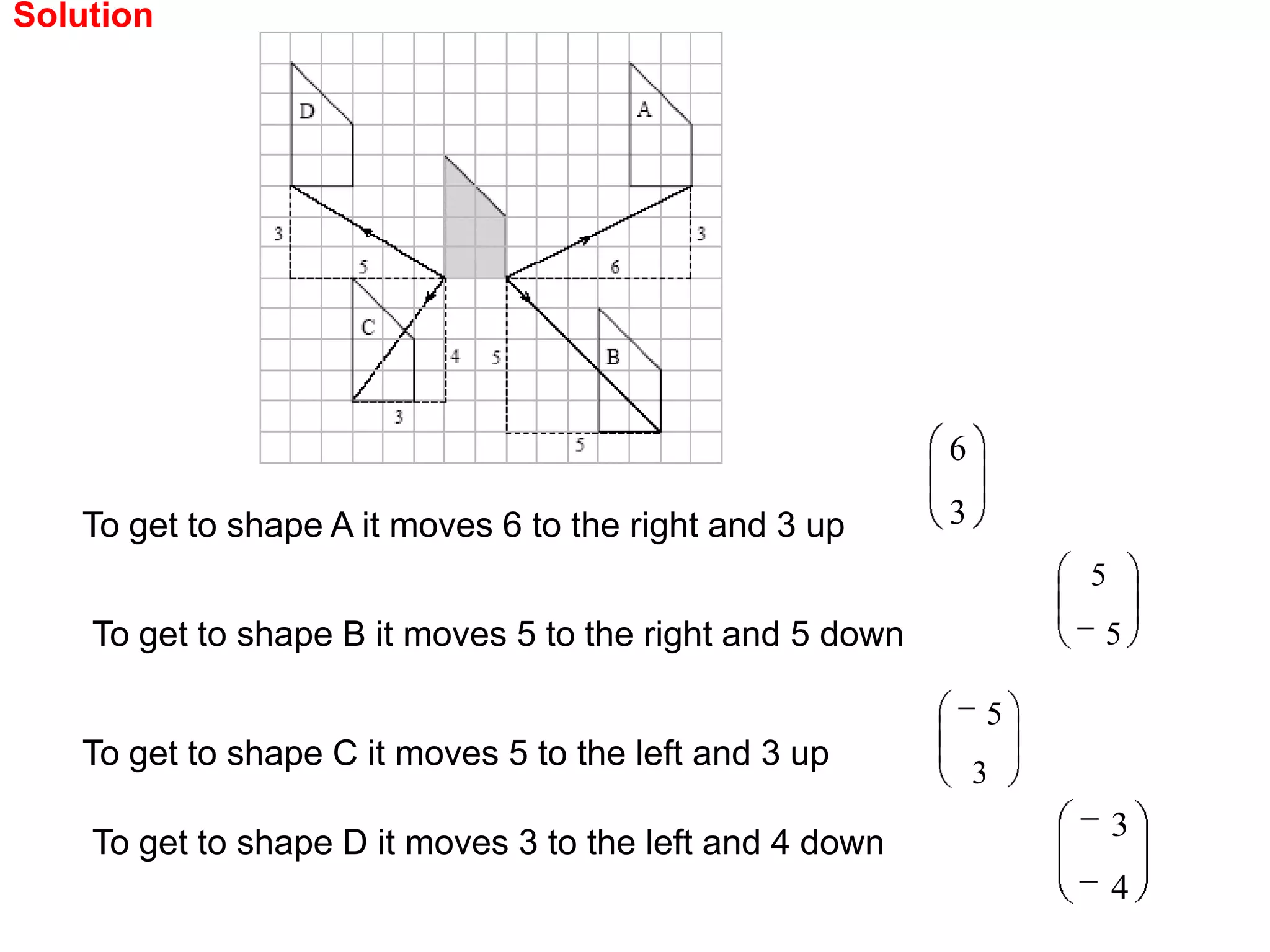
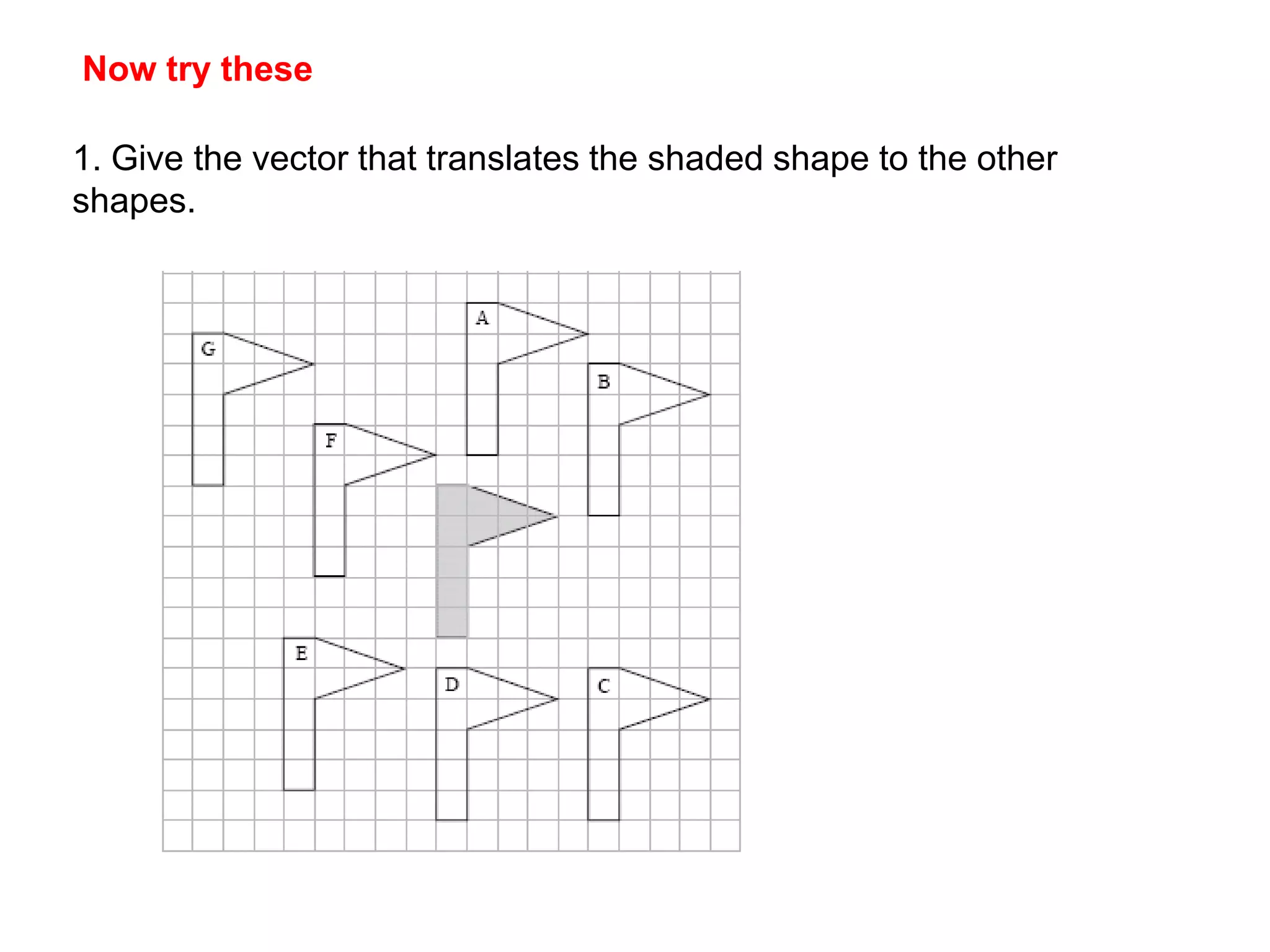
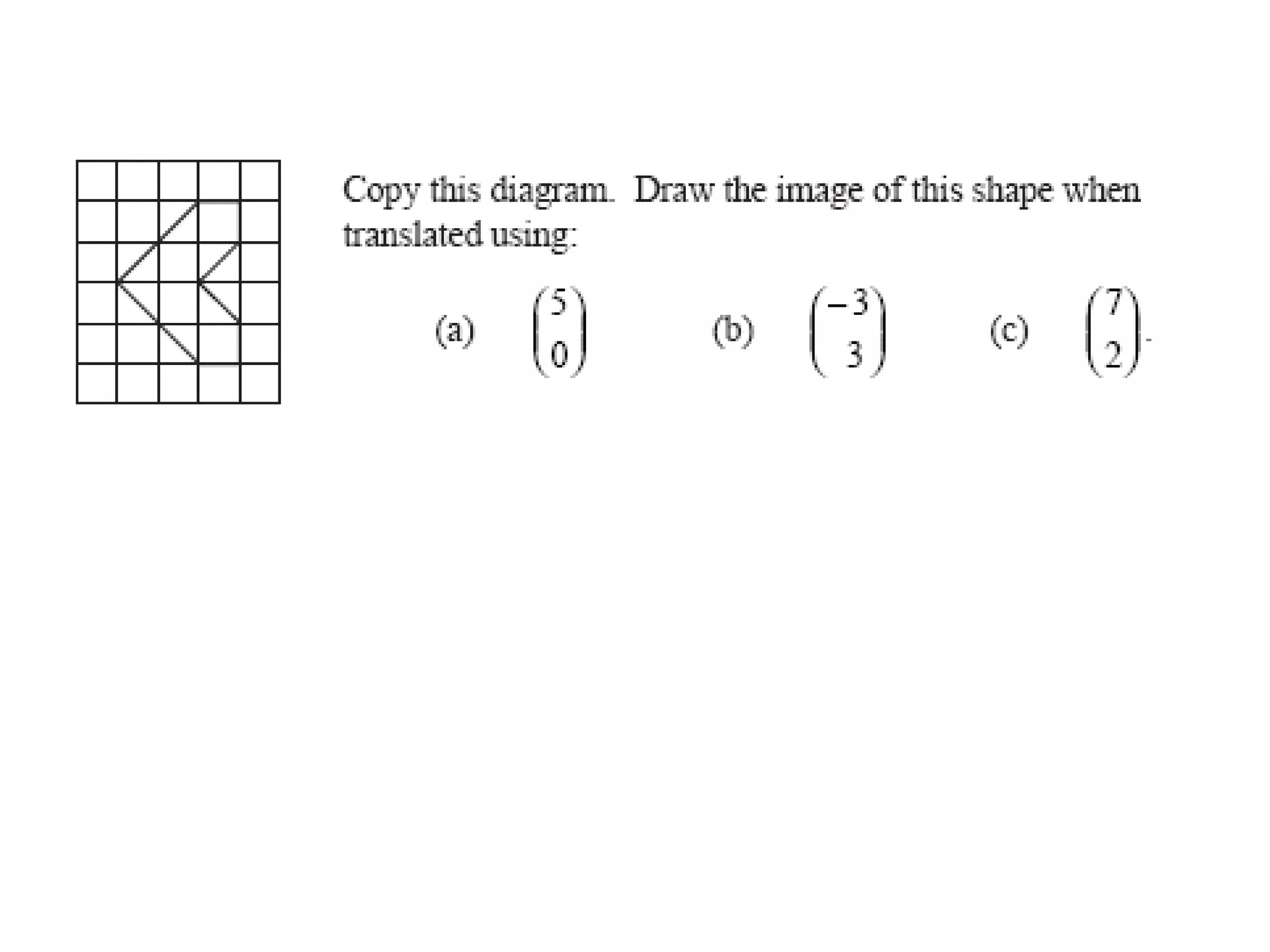
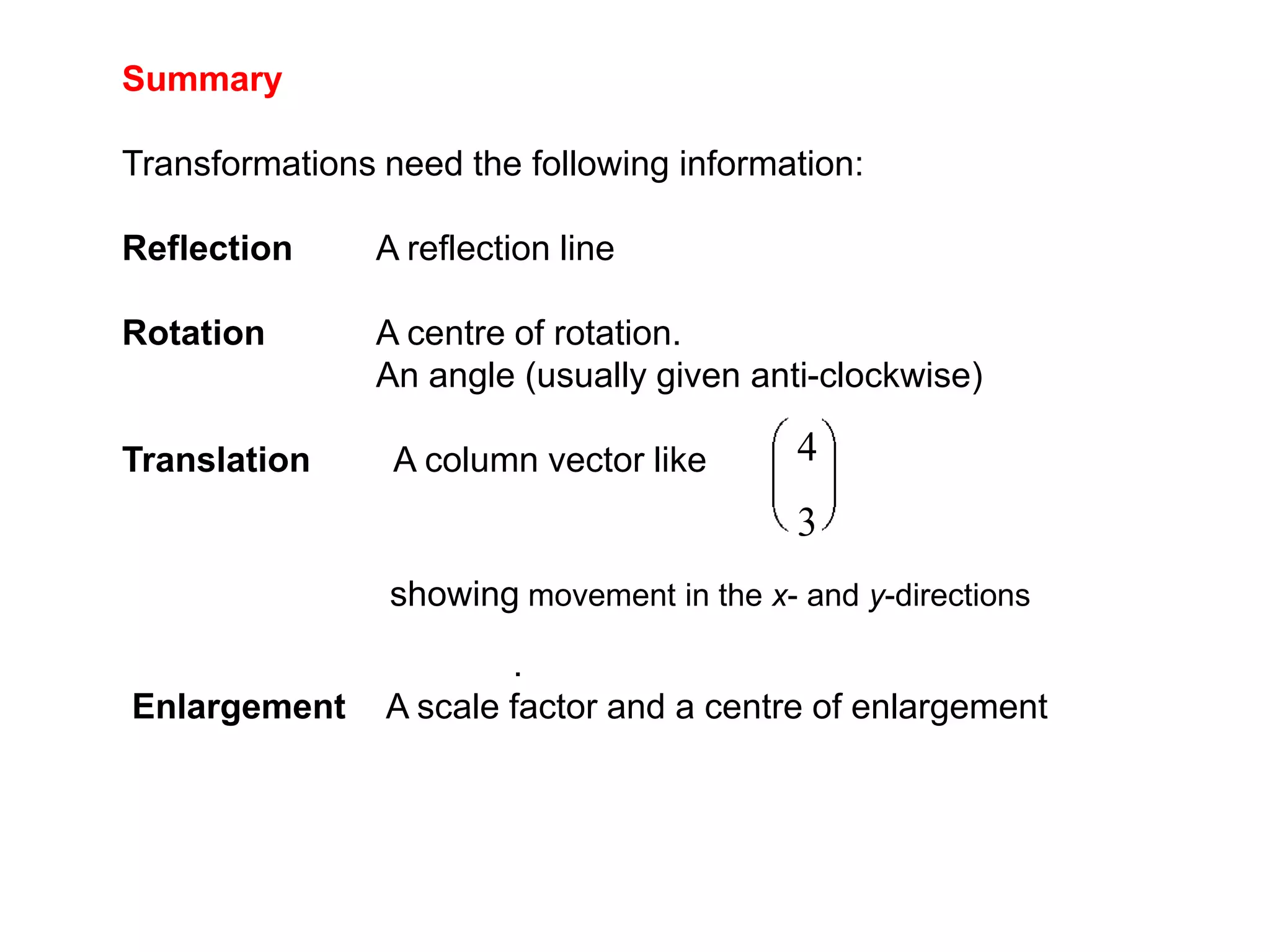
This document discusses different types of geometric transformations including reflections, rotations, translations, and enlargements. It provides examples and explanations of each type of transformation. Reflections require a mirror line and produce a image that is the same distance from the mirror line as the original shape. Rotations occur around a center of rotation when a shape is turned a specified angle. Translations move a shape without changing its size or orientation through a movement described by a vector. Enlargements produce similar shapes that are enlarged or reduced versions of the original through a scale factor from a center of enlargement.

1. TransformationsBTEOTSSSBAT solve problems involving reflection, rotation, translation and enlargement

2. Key wordsTransformationTranslationImageObjectReflectionRotationOriginEnlargementCongruentSimilar

3. A transformation changes a shape.There are four main types of transformations: Reflections,

4. Rotations

5. Enlargements and

6. TranslationReflectionThe triangles above are reflected in the dotted mirror line. The image is the same distance from the mirror line as the object.To describe a reflection we need a mirror line.

7. Now try these 1Draw the image of the objects in (a) and (b) on the sheet – it may go outside of the grid. 2. Draw the triangle ABC such that A is the point (1, 1) B is the point (3, 1) C is the point (1, 2). (a) Reflect the triangle in the x-axis to obtain triangle A1B1C1. What are the co-ordinates of triangle A1B1C1? (b) Reflect the triangle in the y-axis to obtain triangle A2B2C2. What are the co-ordinates of triangle A2B2C2?

8. RotationRotations occur when a shape is rotated a specified angle around a centre of rotation.

9. ExampleRotate this triangle 90° through the origin (0,0)First mark the centre of rotation.Draw around the original shape using tracing paper. Rotate the tracing paper 90° clockwise around the centre of rotation, draw the new position of the image.

10. Now try these 2A triangle’s co-ordinates of the vertices are (2, 1), (1, 6), (2, 3).Rotate it in the following ways (draw your answer on the grid above):(a) 90 about (1, 0)(b) 90 about (0, 1)(c) 90 about (3, 0)(d) 180 about (2, 0)(e) 180 about (0, 0)(f) 270 about (2, 1)(g) 270 about (0, 2)Note:all angles are anti-clockwise, this is how angles are given in rotations unless it says clockwise.

11. EnlargementThe diagram shows two enlargements of an object A. The first is enlarged by a scale factor of 2, the second by a scale factor of 4 from the centre of enlargement O.The distance between O and A´ is 2  OA and the distance between O and A´´ is 4  OA.

12. Example Enlarge the shape ABC with a scale factor of 3 from the centre of enlargement marked.

13. Draw a line from the centre of enlargement going through each vertex of the shape.

14. As the scale factor of enlargement is 3 then:OA´ = 3 OAOB´ = 3OBOC´ = 3 OC

15. Now try these 1. On the grid enlarge the shape by a scale factor of 3.

16. 2. Enlarge the shape with a scale factor of 2 and centre (0,3)

17. 3. T is an enlargement of S from a centre C.On the grid mark the centre C and state the scale factor enlargement.

18. TranslationThe triangle above has been translated. It has moved 4 squares to the right and two squares up. The movement is shown by a vector:movement in the x-directionmovement in the y-directionIn translation the size of the shape does not change, the shape is not rotated or reflected.

19. ExampleDescribe the translation that moves the shaded shape to each of the other shapes.;

20. SolutionTo get to shape A it moves 6 to the right and 3 up To get to shape B it moves 5 to the right and 5 down To get to shape C it moves 5 to the left and 3 up To get to shape D it moves 3 to the left and 4 down

21. Now try these1. Give the vector that translates the shaded shape to the other shapes.

23. Similarity and CongruenceShapes are called congruent when they have the same shape and size. If you translate, rotate or reflect a shape, the new shape will be congruent with the old one. Shapes are called similar when they have the same shape but are different sizes. If you enlarge a shape, the new shape will be similar to the old one.

24. SummaryTransformations need the following information:Reflection A reflection lineRotation A centre of rotation. An angle (usually given anti-clockwise)Translation A column vector like showing movement in the x- and y-directions .Enlargement A scale factor and a centre of enlargement

25. Images borrowed from CIMT’s MEP http://www.cimt.plymouth.ac.uk/projects/mepres/allgcse/allgcse.htm