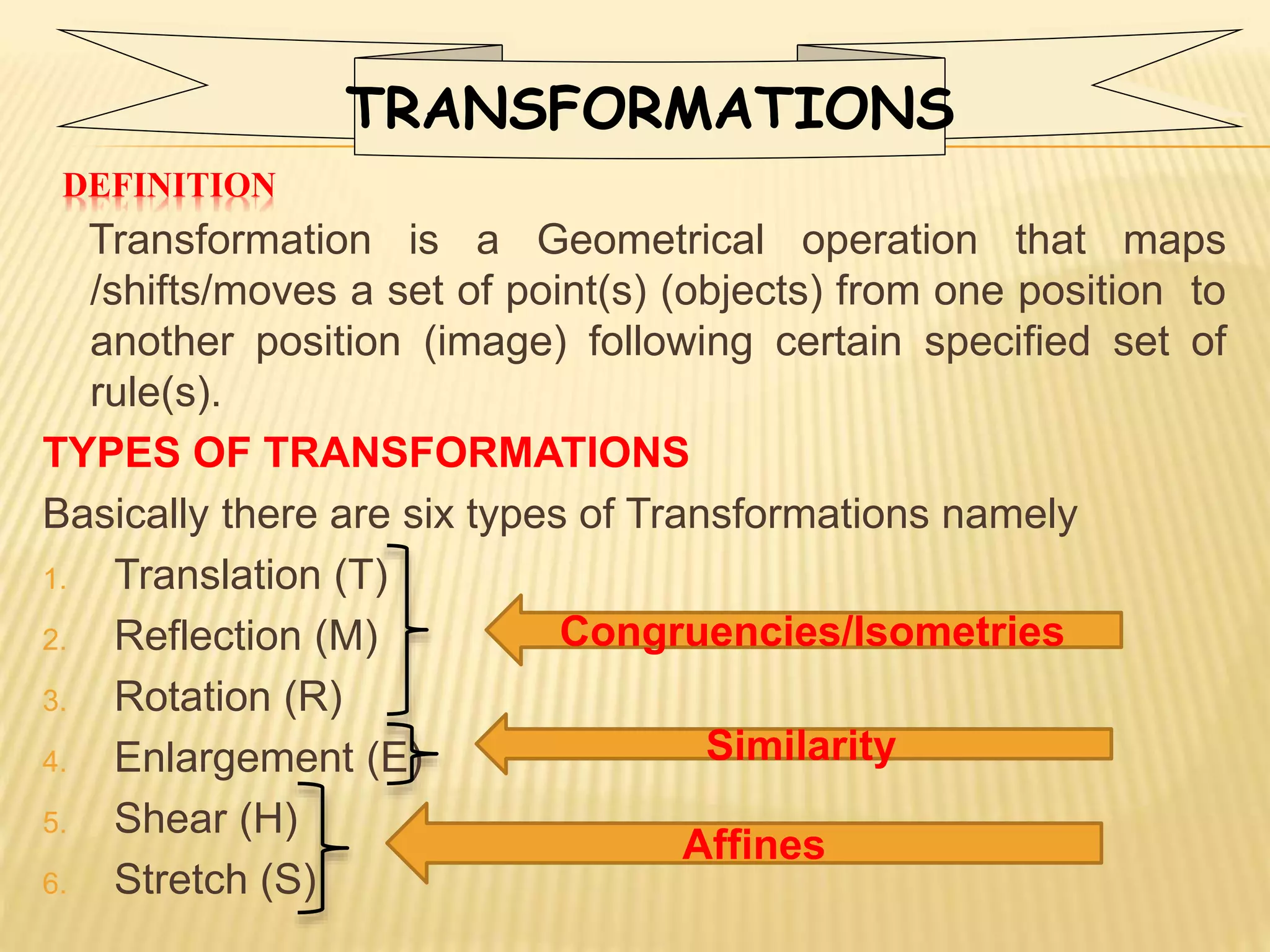
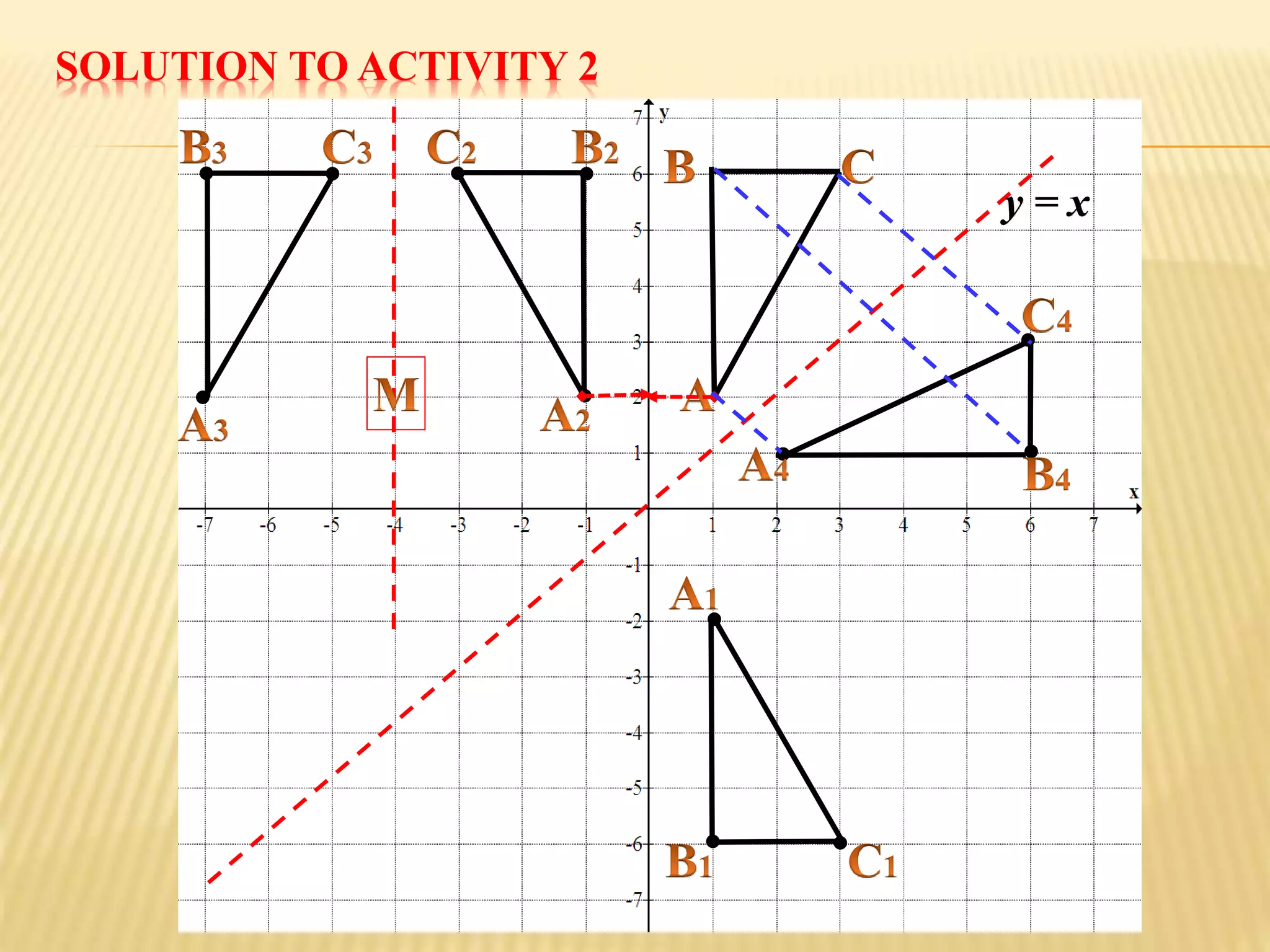
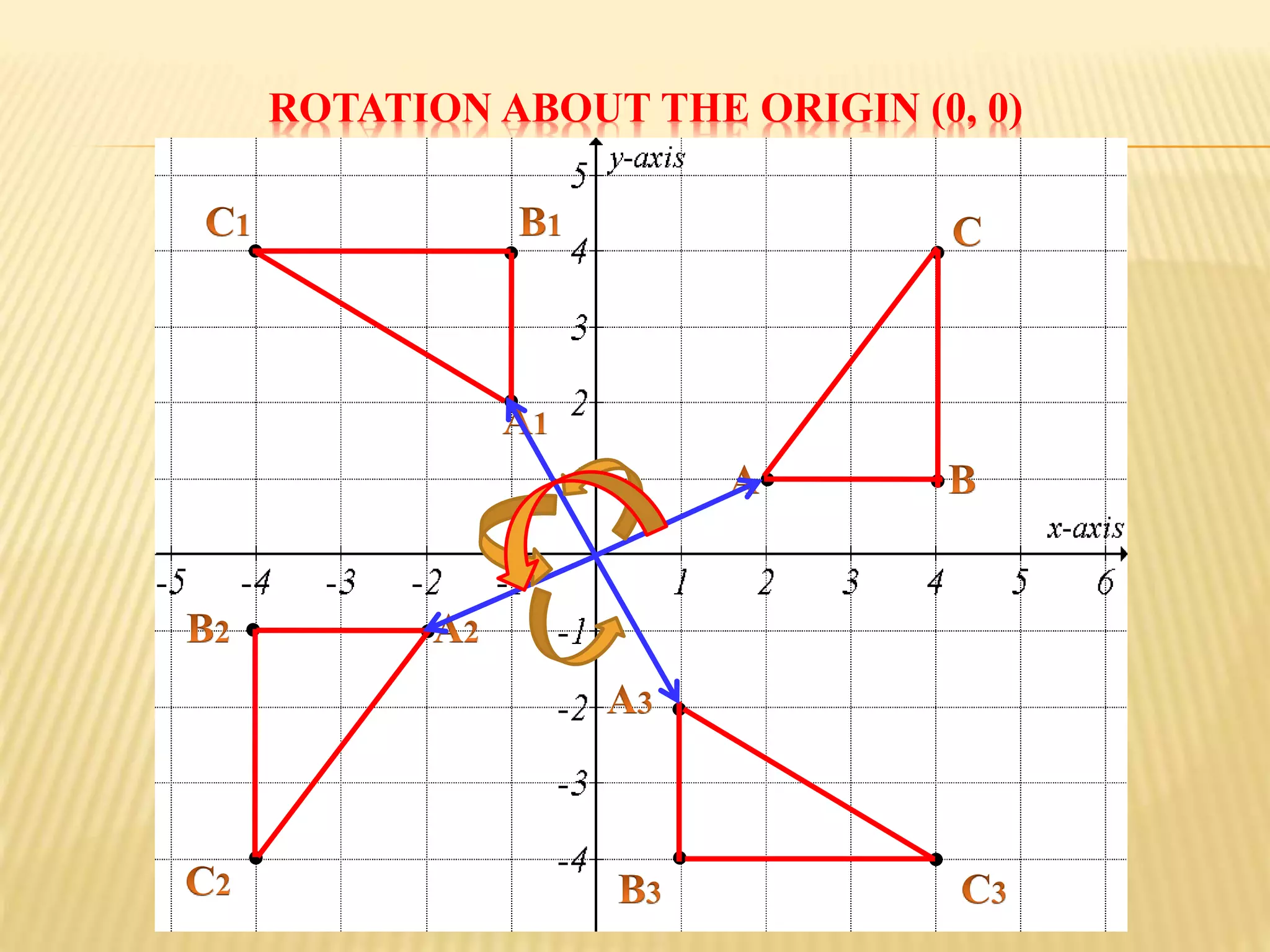
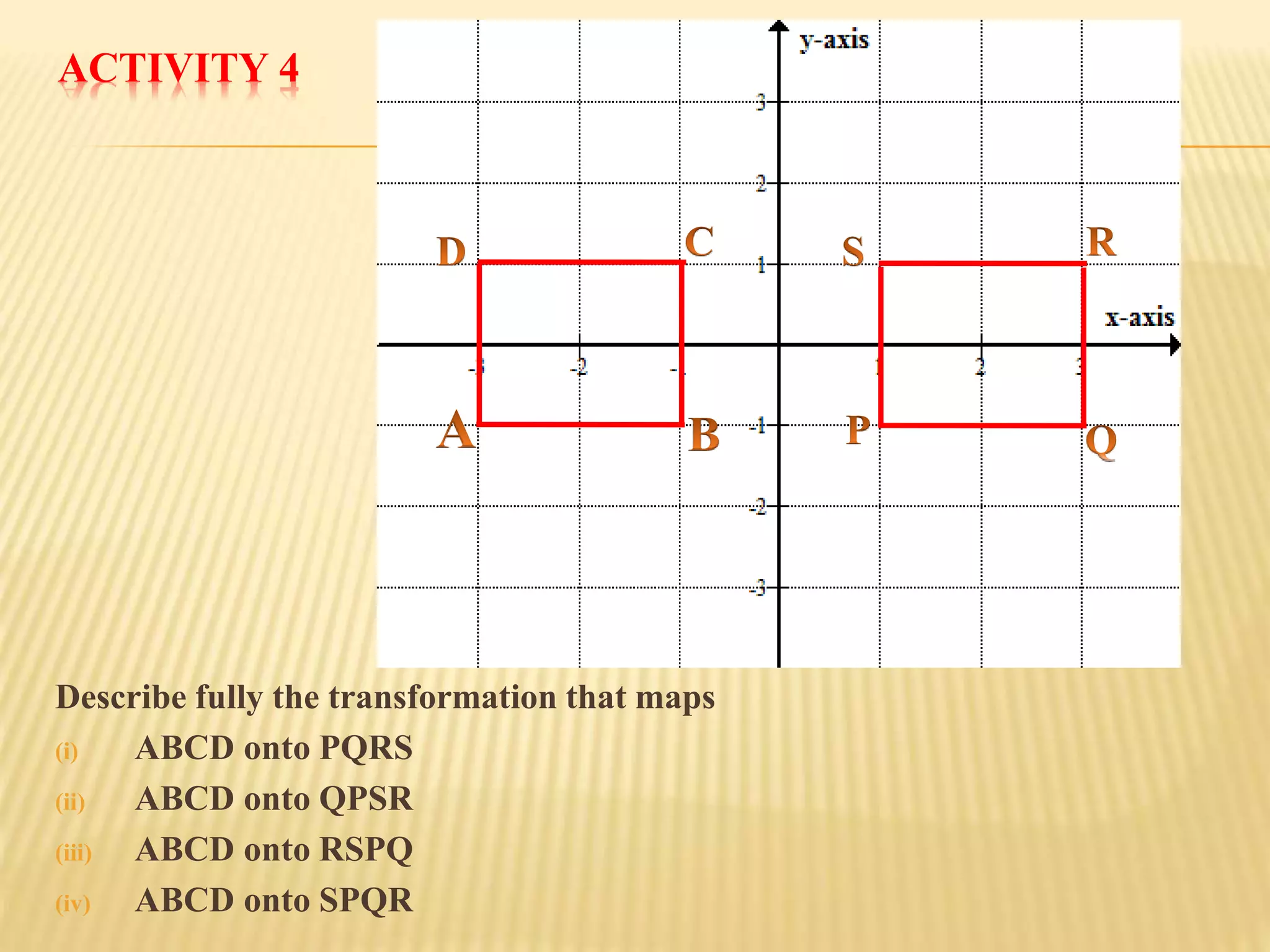
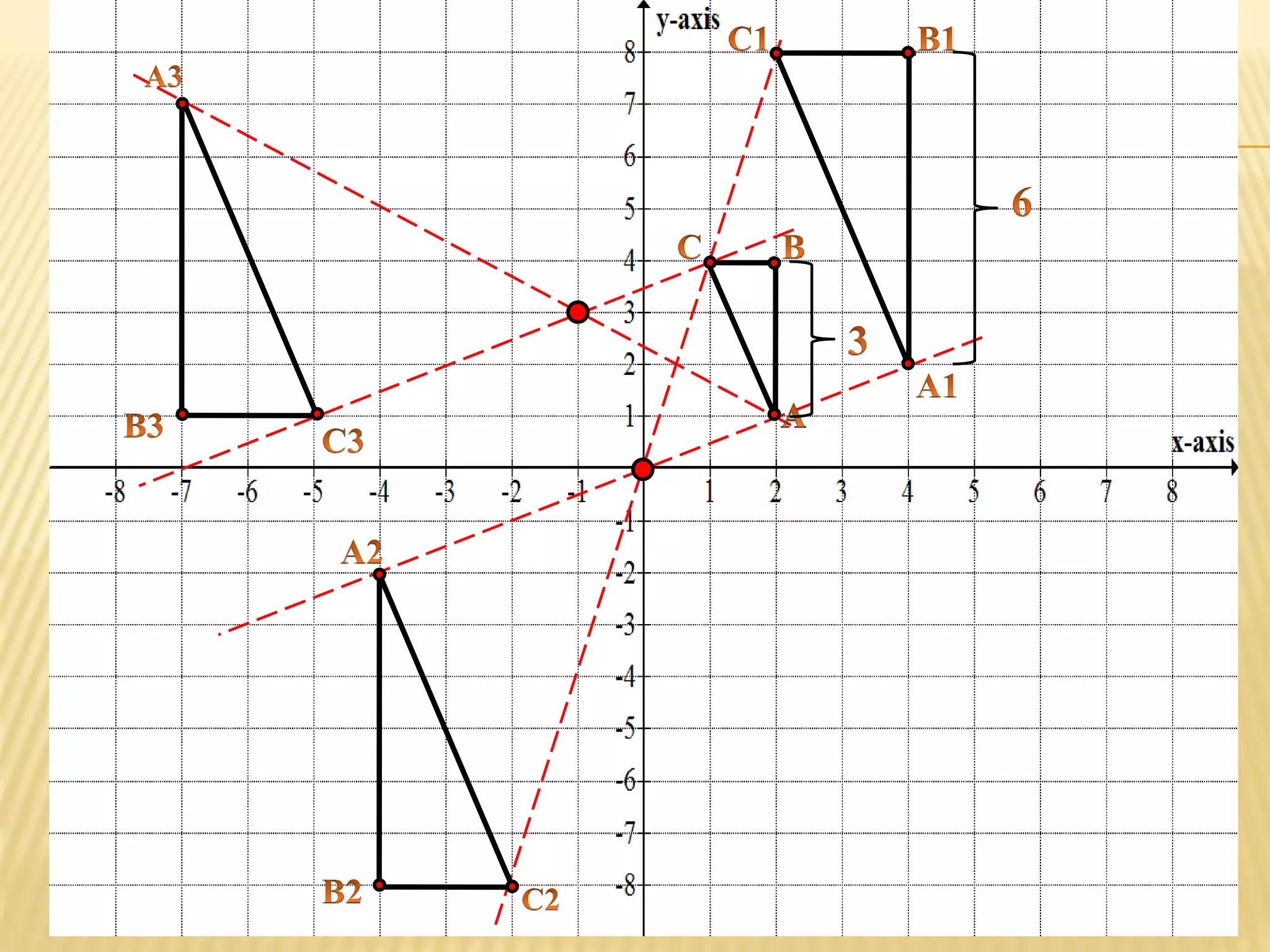
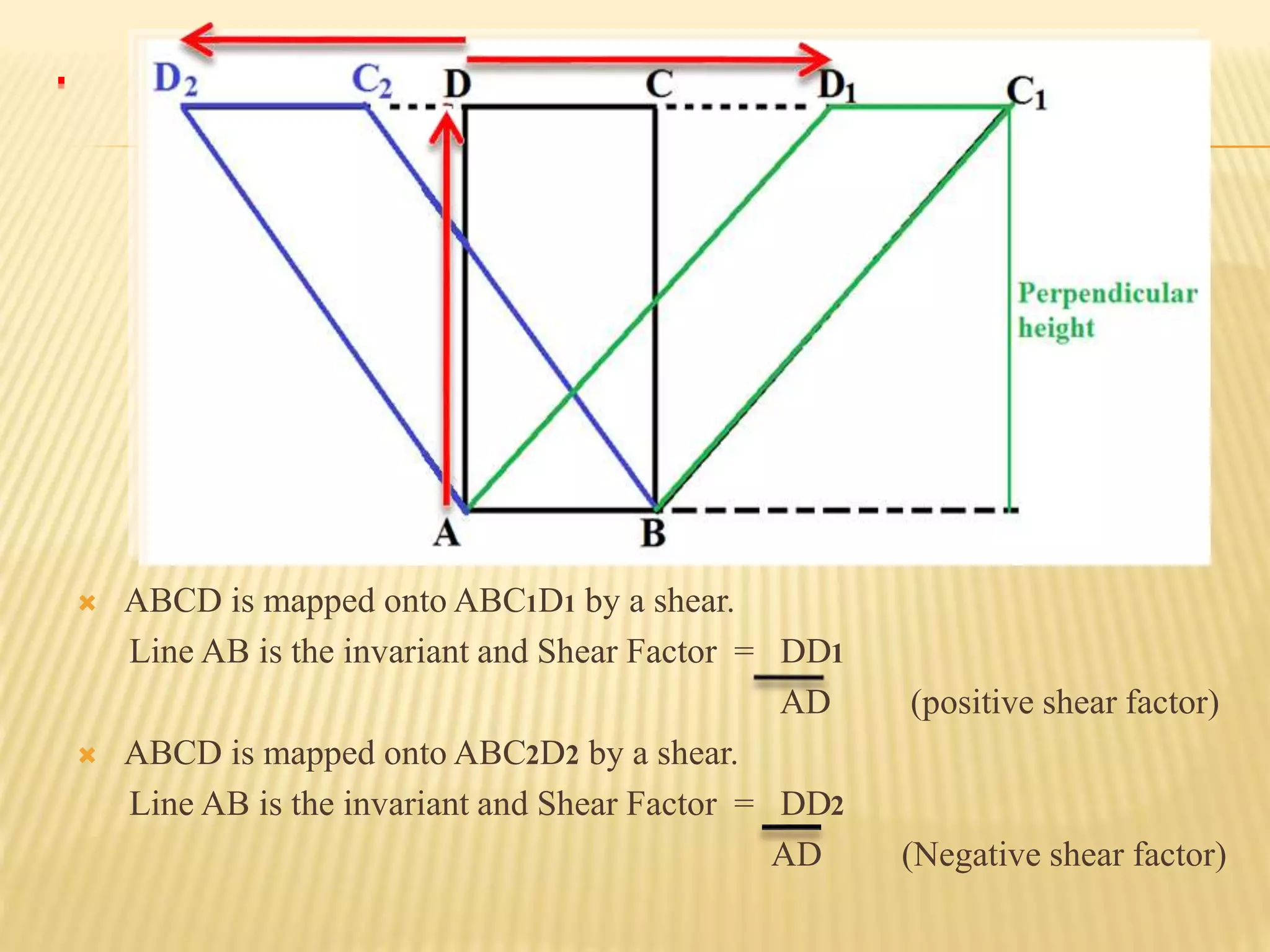
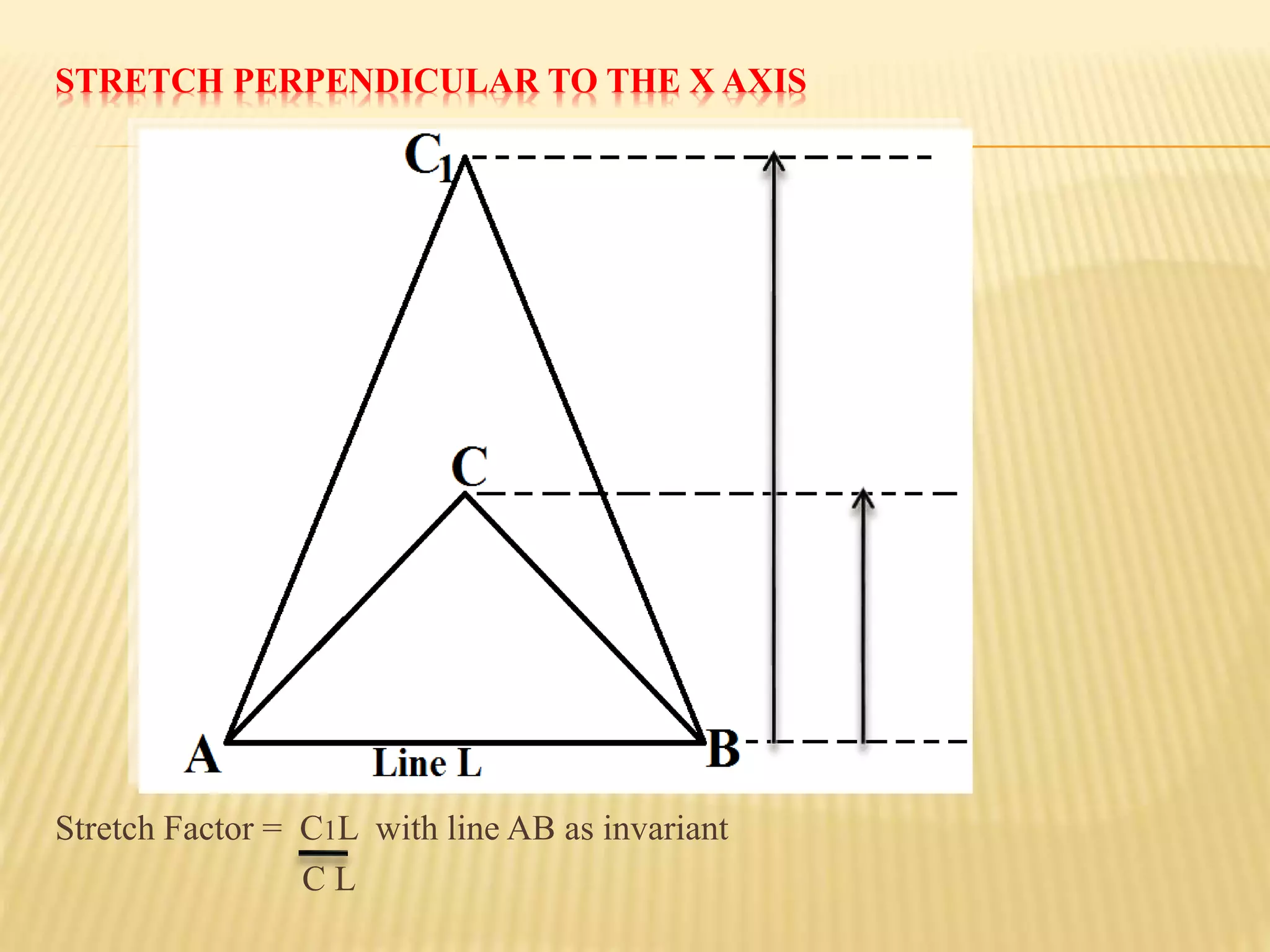
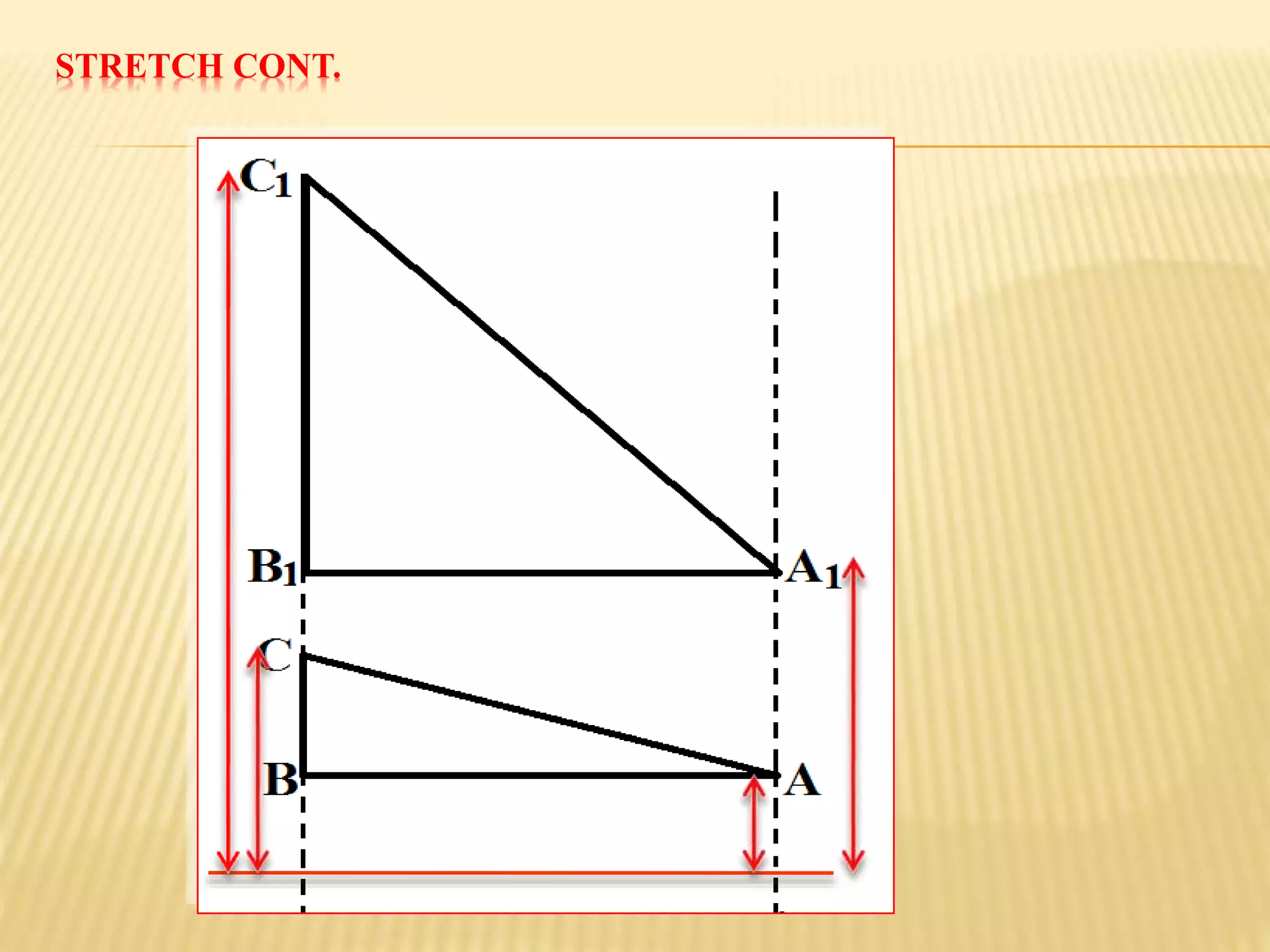
This document provides an overview of transformations presented by Mr. R. Munga, Head of Department for Mathematics at Hillside Secondary School. It defines transformations as geometric operations that map a set of points from one position to another following specified rules. There are six main types of transformations discussed: translation, reflection, rotation, enlargement, shear, and stretch. For each transformation type, the document provides the key properties, describes how to identify and fully specify the transformation, and includes example problems and solutions. The goal is to build students' understanding and ability to recognize, describe, and perform different types of geometric transformations.

1. REPUBLIC OF ZAMBIA
MINISTRY OF EDUCATION, VOCATION TRAINING
AND EARLY EDUCATION

2. PRESENTATION
by
Mr. R. Munga
Head of Department (Mathematics)
Hillside Secondary School.
prdm74@gmail.com
TRANSFORMATIONS

3. PRE REQUISITE KNOWLEDGE
 Coordinate geometry
 Locus
 Congruency and Similarity
 Vectors
 Angle measure
 matrices

4. DEFINITION
Transformation is a Geometrical operation that maps
/shifts/moves a set of point(s) (objects) from one position to
another position (image) following certain specified set of
rule(s).
TYPES OF TRANSFORMATIONS
Basically there are six types of Transformations namely
1. Translation (T)
2. Reflection (M)
3. Rotation (R)
4. Enlargement (E)
5. Shear (H)
6. Stretch (S)
Congruencies/Isometries
Affines
Similarity
TRANSFORMATIONS

5. 1. TRANSLATION ( T )
In a Translation,
1. The object and the image have exactly the same size and
shape. (congruent).
2. The object and the image face the same direction.
A Translation is fully described by a column vector / translation
vector. x
y
It is important to be aware of the positive and negative vector
components of the translation.
Objectives: Identify and name a translation.
Calculate the column Vector
Describing the translation fully.
Calculate coordinates and draw the image or the object on
the Cartesian plane.

6. ACTIVITY 1
(a) Triangle A has coordinates (1, 1), (4, 1) and (1, 2) and Triangle B
has Vertices (3, 4), (6, 4) and (3, 5). Draw and label the
Triangles A and B clearly.
(b) Name the transformation that maps ∆ A onto ∆ B
(c) ∆ A is mapped onto ∆ C by a translation. Write down its column
vector.
(d) ∆ A is mapped onto ∆ D by a translation whose column vector is
- 5
2 Calculate the coordinates of ∆ D, hence draw and label ∆ D
clearly.
(e) Describe fully the single transformation that maps ∆ D onto ∆ B

7. Solution to Activity 1

8. SOLUTION
(a) On the graph
(b) Translation
(c) Column Vector = Image coordinate – Object coordinate.
Column Vector = 0 - 4 = -4
-4 1 -5
(d) -6 = x - 1
2 y 1 ( x , y ) = (- 4, 3 )
(e) ∆ D onto ∆ B by a translation whose column vector is 7
1

9. 2. REFLECTION (M)
In a Reflection,
1. The object and the image have exactly the same size and shape.
(congruent).
2. The object and the image face the exact opposite direction.
3. A refection is fully described by the equation of the mirror line ( Usually
drawn as a dotted line)
4. The mirror line is the perpendicular bisector of the two corresponding
points ( from the Object and the Image)
Objectives: - Identify and name a reflection.
- Calculate the equation and draw the mirror line.
- Describe the reflection fully.
- Calculate coordinates and draw the image or the object on the
Cartesian plane.
Introduction of matrices for reflection in the x-axis and the y-axis.

10. ACTIVITY 2
(i) Name the transformation that maps triangle ∆ABC onto triangle
∆ A1B1C1.
(ii) ∆ ABC is reflected onto ∆A2B2C2 by a reflection in the y-axis.
Draw and label ∆A2B2C2.
(iii) ∆A2B2C2 is reflected onto ∆A3B3C3 in the line M. Draw, label
and write down the equation of line M.
(iv) ∆ABC is reflected onto ∆A4B4C4 in the line y = x. Draw and
label ∆A4B4C4
(v) Name the transformation that maps ∆ABC onto ∆A3B3C3.
(vi) Name the transformation that maps ∆A4B4C4 onto ∆A2B2C2.

11. SOLUTION TO ACTIVITY 2
y = x

12. 3. ROTATION (R)
In a Rotation,
1. The object and the image have exactly the same size and shape.
(congruent).
2. The direction of object and the image is neither the same nor direct
opposite.
A Rotation is fully described by the direction, angle and Centre of rotation
Objectives: - Identify and name a rotation.
- Find the centre by construction and measure the angle of
rotation Clockwise or anticlockwise.
- Describe the rotation fully.
- Calculate coordinates and draw the image
or the object on the Cartesian plane.
The angles matrices must include +90, 180 and - 90. centre (0, 0)

13. ROTATION ABOUT THE ORIGIN (0, 0)

14. MATRICES REPRESENTING ROTATION ABOUT (0,0)
 The Matrix 0 -1 represents an anticlockwise rotation of 90
1 0 about ( 0, 0 )
 The Matrix -1 0 represents an anticlockwise rotation of 180
0 -1 about ( 0, 0 )
 The Matrix 0 1 represents an clockwise rotation of 90
-1 0 about ( 0, 0 )

15. ACTIVITY 3
(i) ∆ABC is mapped onto ∆ PQR by an anticlockwise rotation of 90 Degrees.
Find the centre of rotation.
(ii) ∆ ABC is mapped onto ∆A1B1C1 by a clockwise rotation of 90 about (0,0).
Draw and label ∆A1B1C1.
(iii) ∆PQR is mapped onto ∆P1Q1R by a clockwise rotation of 90. Draw and label
∆P1Q1R.
(iv) Name the transformation that maps ∆ABC onto ∆P1Q1R.
(v) ∆P1Q1R. Is translated onto ∆A2B2C2 by a column vector 2
Draw and label clearly ∆A2B2C2. - 6
(i) Describe fully the transformation that maps ∆A2B2C2 onto ∆A1B1C1.

17. ACTIVITY 4
Describe fully the transformation that maps
(i) ABCD onto PQRS
(ii) ABCD onto QPSR
(iii) ABCD onto RSPQ
(iv) ABCD onto SPQR

18. SOLUTIONS TO ACTIVITY 4
(i) Translation
Column Vector = 4
0
(ii) Reflection
y-axis (x = 0 ) as the mirror line.
(iii) Rotation of 180 degrees.
Centre ( 0, 0 )
(iv) Clockwise rotation of 90 Degrees.
Centre ( 0, -2)

19. 3. ENLARGEMENT (E)
In an Enlargement,
1. The object and the image are Similar i.e. corresponding sides are in
the same ratio.
2. The direction of object and the image can either be the same or
opposite.
An Enlargement is fully described by the centre and Scale factor
Objectives: - Identify and name an Enlargement.
- Find the Scale factor of an Enlargement
- Find the centre of enlargement
- Recall the matrix for enlargement Centre (0,0) and apply it
to find the coordinates of the Image or object.
The matrix k 0 represents an enlargement centre (0,0) and Scale factor k
0 k

20. ACTIVITY 5
(a) Draw x and y axes for – 8 ≤ x ≤ 8 and – 8 ≤ y ≤ 8
(b) Draw and clearly label ∆ABC for which A(2,1), B(2,4) and C(1,4)
(c) ∆ABC is mapped onto ∆A1B1C1 by a matrix 2 0
0 2
(d) Describe fully the Transformation that maps ∆ABC onto
∆A1B1C1
(e) ∆ABC is mapped onto ∆A2B2C2 by an Enlargement centre (0,0)
and scale factor – 2.
(f) ∆ABC is mapped onto ∆A3B3C3 by an Enlargement. Find the
centre of enlargement and the scale factor.
(g) Describe fully the transformation that maps ∆A2B2C2 onto
∆A3B3C3.

22. SHEAR (H)
 In a shear the Object is sheared onto the Image with its area and perpendicular
height maintained.
 In a Shear the movements of the points is parallel to the invariant line.
 A shear is fully described by the equation of the invariant line and the shear
factor ( ± k ).
Objectives: - Identify and name a Shear.
- Find the Shear factor and the equation of the Invariant line.
- Recall the matrix for Shear x-axis / y-axis as the invariant
line and use it to find the coordinates of the Image or object.
The matrix 1 k represents a shear x-axis as the invariant and Shear factor k
0 1
The matrix 1 0 represents a shear y-axis as the invariant and Shear factor k
k 1

23. .
 ABCD is mapped onto ABC1D1 by a shear.
Line AB is the invariant and Shear Factor = DD1
AD (positive shear factor)
 ABCD is mapped onto ABC2D2 by a shear.
Line AB is the invariant and Shear Factor = DD2
AD (Negative shear factor)

24. SHEAR PARALLEL TO THE X-AXIS.
P Q

25. 6. STRETCH (S)
 A Stretch is an Enlargement in one direction.
 In a stretch the movement of points is perpendicular to the Invariant line.
 A stretch is fully described by the equation of the invariant line and the Stretch
factor ( ± k )
Objectives:- Identify and name a Stretch.
- Find the Stretch factor and equation of the Invariant line.
- Recall the matrix for Stretch x-axis/ y-axis as the invariant line and
use it to find the coordinates of the Image or object.
The matrix 1 0 represents a stretch x-axis as the invariant and Shear factor k
0 k
The matrix k 0 represents a stretch y-axis as the invariant and Shear factor k
0 1

26. STRETCH PERPENDICULAR TO THE X AXIS
Stretch Factor = C1L with line AB as invariant
C L

27. STRETCH CONT.

28. STRETCH CONT.
 In general k = area of image
area of object
 Invariant line parallel to the y-axis
 Invariant line parallel to the x - axis

29. Thank you for your participation
and Contributions