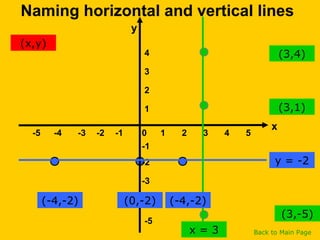
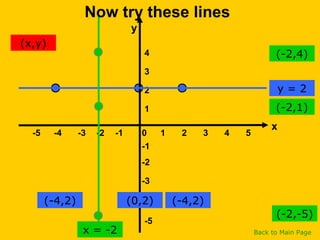
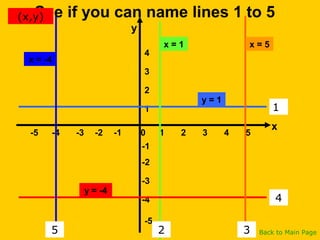
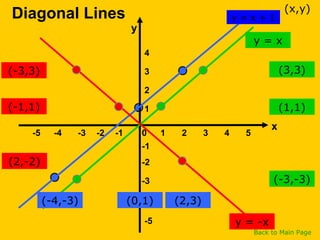
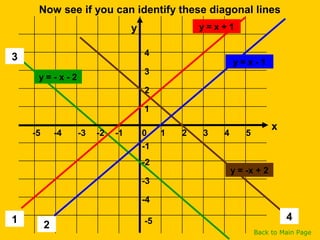
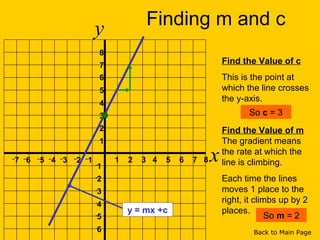
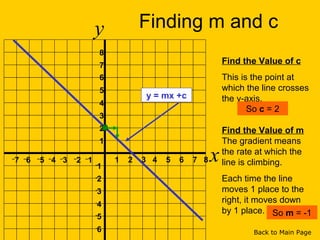
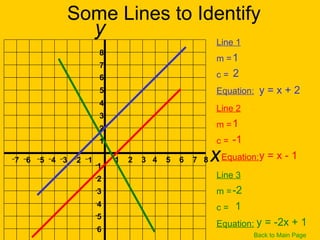
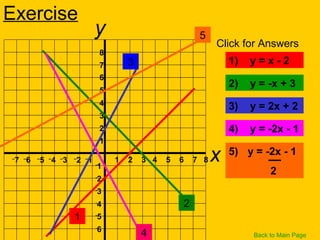
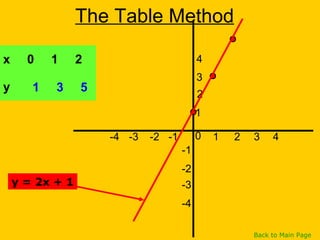
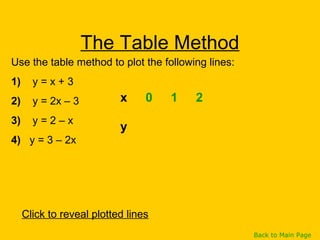
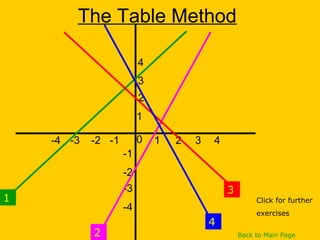
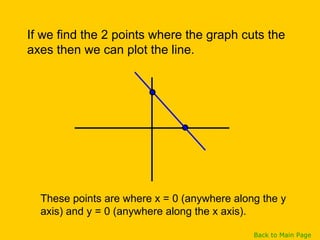
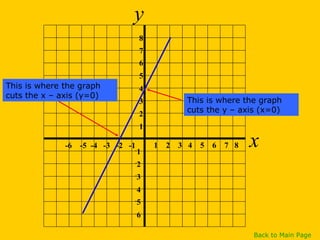
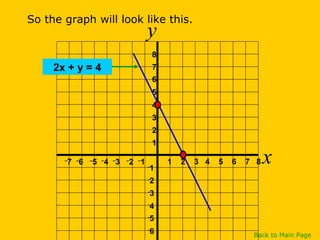
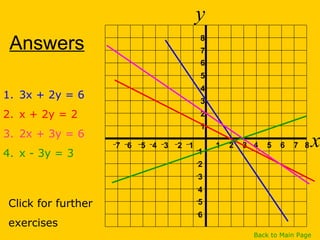
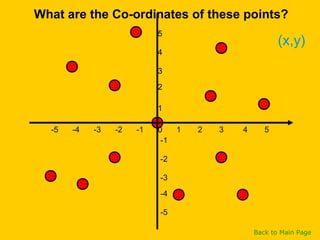
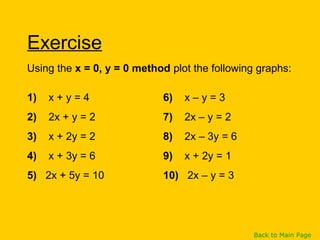This document discusses straight line graphs and various methods for plotting straight lines on a graph. It covers identifying horizontal, vertical and diagonal lines, writing equations in y=mx+c form, using a table method to plot lines by substituting x-values, and using the x=0, y=0 method to find two points and plot a line from its equation. Exercises are provided for students to practice identifying and plotting different types of straight lines.

1. Straight Line Graphs

2. Straight Line Graphs
Sections
1) Horizontal, Vertical and Diagonal Lines
(Exercises)
2) y = mx + c
(Exercises : Naming a Straight Line
Sketching a Straight Line)
3) Plotting a Straight Line - Table Method
(Exercises)
4) Plotting a Straight Line – X = 0, Y = 0 Method
(Exercises)
5) Supporting Exercises
Co-ordinates Negative Numbers Substitution

3. x
y
1
-5
-4
-3
-2
-1
4
3
2
1
-5 -4 -3 -2 0 2 3 54-1
Naming horizontal and vertical lines
(-4,-2) (0,-2) (-4,-2)
y = -2
(3,4)
(3,1)
(3,-5)
x = 3
(x,y)
Back to Main Page

4. 1
-5
-4
-3
-2
-1
4
3
2
1
-5 -4 -3 -2 0 2 3 54-1
Now try these lines
(-4,2) (0,2) (-4,2)
y = 2
(-2,4)
(-2,1)
(-2,-5)
x = -2
(x,y)
Back to Main Page
y
x

5. -5
-4
-3
-2
-1
4
3
2
1
1-5 -4 -3 -2 0 2 3 54-1
See if you can name lines 1 to 5(x,y)
1
5 3
4
2 Back to Main Page
y
x
y = 1
x = 1 x = 5
y = -4
x = -4

6. 1
-5
-4
-3
-2
-1
4
3
2
1
-5 -4 -3 -2 0 2 3 54-1
Diagonal Lines
(-4,-3) (0,1) (2,3)
(3,3)
(1,1)
(-3,-3)
y = -x
(x,y)
Back to Main Page
(2,-2)
(-1,1)
(-3,3)
y = x
y = x + 1
y
x

7. Back to Main Page
1
2
1
-5
-4
-3
-2
-1
4
3
2
1
-5 -4 -3 -2 0 2 3 54-1
3
4
Now see if you can identify these diagonal lines
x
y
y = x - 1
y = x + 1
y = - x - 2
y = -x + 2

8. y = mx + c
Every straight line can be written in this form. To do this the
values for m and c must be found.
y = mx + c
c is known as the intercept
m is known as the gradient
Back to Main Page

9. y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
Find the Value of c
This is the point at
which the line crosses
the y-axis.
Find the Value of m
The gradient means
the rate at which the
line is climbing.
Each time the lines
moves 1 place to the
right, it climbs up by 2
places.
Finding m and c
y = 2x +3y = mx +c
So c = 3
So m = 2
Back to Main Page

10. y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
Find the Value of c
This is the point at
which the line crosses
the y-axis.
Find the Value of m
The gradient means
the rate at which the
line is climbing.
Each time the line
moves 1 place to the
right, it moves down
by 1 place.
Finding m and c
y = 2x +3y = mx +c
So c = 2
So m = -1
Back to Main Page

11. y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
Line 1
m =
c =
Equation:
Some Lines to Identify
Line 2
m =
c =
Equation:
1
2
y = x + 2
Line 3
m =
c =
Equation:
1
-1
y = x - 1
-2
1
y = -2x + 1
Back to Main Page

12. y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
Exercise
Back to Main Page
Click for Answers
1
2
3
5
4
1) y = x - 2
2) y = -x + 3
3) y = 2x + 2
4) y = -2x - 1
5) y = -2x - 1
2

13. Further Exercise
Sketch the following graphs by using y=mx + c
1) y = x + 4
2) y = x - 2
3) y = 2x + 1
4) y = 2x – 3
5) y = 3x – 2
6) y = 1 – x
7) y = 3 – 2x
8) y = 3x
9) y = x + 2
2
10) y = - x + 1
2
Back to Main Page

14. The Table Method
We can use an equation of a line to plot a graph by
substituting values of x into it.
Example
y = 2x + 1
x = 0 y = 2(0) +1 y = 1
x = 1 y = 2(1) +1 y = 3
x = 2 y = 2(2) +1 y = 5
Now you just have to plot the points on to a graph!
Back to Main Page
x 0 1 2
y 1 3 5

15. The Table Method
0 1-1 432-2-3-4
-1
-2
-3
-4
1
2
3
4
y = 2x + 1
Back to Main Page
x 0 1 2
y 1 3 5

16. The Table Method
Use the table method to plot the following lines:
1) y = x + 3
2) y = 2x – 3
3) y = 2 – x
4) y = 3 – 2x
Click to reveal plotted lines
Back to Main Page
x 0 1 2
y

17. The Table Method
0 1-1 432-2-3-4
-1
-2
-3
-4
1
2
3
4
4
3
1
2 Back to Main Page
Click for further
exercises

18. Further Exercise
Using the table method, plot the following graphs.
1) y = x + 2
2) y = x – 3
3) y = 2x + 4
4) y = 2x – 3
5) y = 3x + 1
6) y = 3x – 2
7) y = 1 – x
8) y = 1 – 2x
9) y = 2 – 3x
10) y = x + 1
2
Back to Main Page
2

19. This method is used when x and y are on the same side.
Example: x + 2y = 4
The x = 0, y = 0 Method
To draw a straight line we only need 2 points to join
together.
Back to Main Page

20. These points are where x = 0 (anywhere along the y
axis) and y = 0 (anywhere along the x axis).
If we find the 2 points where the graph cuts the
axes then we can plot the line.
Back to Main Page

21. y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
-6 -5 -4 -3 -2 -1-
1
-
2
-
3
-
4
-
5
-
6
This is where the graph
cuts the y – axis (x=0)
This is where the graph
cuts the x – axis (y=0)
Back to Main Page

22. By substituting these values into the equation we
can find the other half of the co-ordinates.
Back to Main Page

23. Example
Question: Draw the graph of 2x + y = 4
Solution
x = 0
2(0) + y = 4
y = 4
1st
Co-ordinate = (0,4)
y = 0
2x + 0 = 4
2x = 4
x = 2
2nd
Co-ordinate = (2,0)
Back to Main Page

24. So the graph will look like this.
y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
2x + y = 4
Back to Main Page

25. Exercise
Plot the following graphs using the x=0, y=0 method.
1) x + y = 5
2) x + 2y = 2
3) 2x + 3y = 6
4) x + 3y = 3
Click to reveal plotted lines
Back to Main Page

26. Answers
y
x1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
–
7 –
6 –
5 –
4 –
3 –
2 –
1 -
1
-
2
-
3
-
4
-
5
-
6
1. 3x + 2y = 6
2. x + 2y = 2
3. 2x + 3y = 6
4. x - 3y = 3
Click for further
exercises
Back to Main Page

27. Exercise
1) x + y = 4
2) 2x + y = 2
3) x + 2y = 2
4) x + 3y = 6
5) 2x + 5y = 10
6) x – y = 3
7) 2x – y = 2
8) 2x – 3y = 6
9) x + 2y = 1
10) 2x – y = 3
Back to Main Page
Using the x = 0, y = 0 method plot the following graphs:

28. What are the Co-ordinates of these points?
-1
1
-5
-4
-3
-2
5
4
3
2
1
-5 -4 -3 -2 0 2 3 54-1
(x,y)
Back to Main Page

29. Negative Numbers
(1) 2 + 3 (2) 6 - 5 (3) 3 - 7 (4) -2 + 6
(5) -1 - 2 (6) -4 + 5 (7) -2 - 2 (8) 0 – 4
(9) -3 + 6 (10) -4 - 1 (11) 6 - 8 (12) -5 - 2
(13) -8 + 4 (14) -5 - (- 2) (15) 0 - (- 1)
(16) 7 - 12 + 9 (17) -4 - 9 + -2 (18) 14 - (- 2)
(19) -45 + 17 (20) 4 - 5½
Addition and Subtraction
Back to Main Page

30. Negative Numbers
(1) 4 x -3 (2) -7 x -2
(3) -5 x 4 (4) 28 ÷ -7
(5) -21 ÷ -3 (6) -20 ÷ 5
(7) -2 x 3 x 2 (8) -18 ÷ -3 x 2
(9) -2 x -2 x -2 (10) 2.5 x -10
Multiplication and Division
Back to Main Page

31. Substituting Numbers into Formulae
Exercise
Substitute x = 4 into the following formulae:
1) x – 2
2) 2x
3) 3x + 2
4) 1 – x
5) 3 – 2x
6) 4 - 2x
7) x - 3
2
8) 3 - x
2
9) 2x – 6
Click forward to reveal answers
2
8
14
-3
-5
-4
-1
1
2
Back to Main Page

32. Substituting Negative Numbers into Formulae
Exercise
Substitute x = -1 into the following formulae:
1) x – 2
2) 2x
3) 3x + 2
4) 1 – x
5) 3 – 2x
6) 4 - 2x
7) x - 3
2
8) 3 - x
2
9) 2x – 6
Click forward to reveal answers
-3
-2
-1
2
5
6
-3½
3½
-8
Back to Main Page