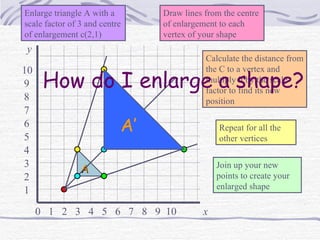
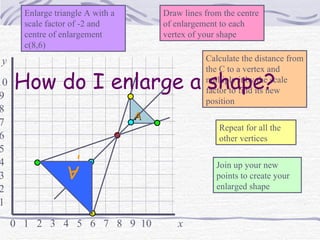
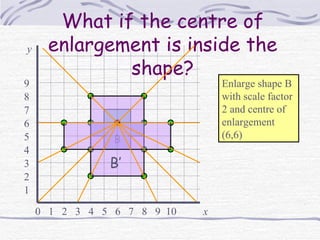
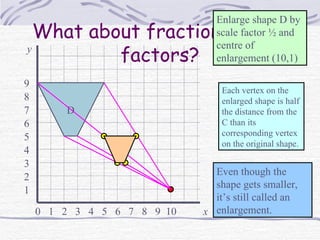
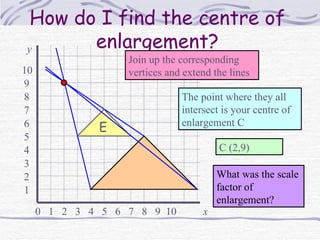
The document discusses enlargements of shapes using scale factors and centers of enlargement. It explains that the scale factor determines the size of the enlargement relative to the original shape. The center of enlargement determines where the enlarged shape is positioned. It provides examples of enlarging triangles with different scale factors and centers, including when the center is inside the original shape or when the scale factor is fractional. It also describes how to find the center of enlargement given a original and enlarged shape.

1. Enlargements Objectives To be able to: Enlarge shapes given a scale factor and centre of enlargement. Find centres of enlargement

2. Scale factors and centres of enlargement The size of an enlargement is described by its scale factor. For example, a scale factor of 2 means that the new shape is twice the size of the original , a scale factor of (-2) means that the new shape is reflect twice the size of the original. The position of the enlarged shape depends on the centre of enlargement.

3. How do I enlarge a shape? Enlarge triangle A with a scale factor of 3 and centre of enlargement c(2,1) Draw lines from the centre of enlargement to each vertex of your shape Calculate the distance from the C to a vertex and multiply it by the scale factor to find its new position Repeat for all the other vertices Join up your new points to create your enlarged shape 0 1 2 3 4 5 6 7 8 9 10 x 1 9 8 7 6 5 4 3 2 y 10 A A’

4. How do I enlarge a shape? Enlarge triangle A with a scale factor of -2 and centre of enlargement c(8,6) Draw lines from the centre of enlargement to each vertex of your shape Calculate the distance from the C to a vertex and multiply it by the scale factor to find its new position Repeat for all the other vertices Join up your new points to create your enlarged shape 0 1 2 3 4 5 6 7 8 9 10 x 1 9 8 7 6 5 4 3 2 y 10 A A’

5. What if the centre of enlargement is inside the shape? Enlarge shape B with scale factor 2 and centre of enlargement (6,6) B B’ 0 1 2 3 4 5 6 7 8 9 10 x 1 9 8 7 6 5 4 3 2 y

6. What about fractional scale factors? D Enlarge shape D by scale factor ½ and centre of enlargement (10,1) Even though the shape gets smaller, it’s still called an enlargement. Each vertex on the enlarged shape is half the distance from the C than its corresponding vertex on the original shape. 0 1 2 3 4 5 6 7 8 9 10 x 1 9 8 7 6 5 4 3 2 y

7. How do I find the centre of enlargement? Join up the corresponding vertices and extend the lines The point where they all intersect is your centre of enlargement C C (2,9) What was the scale factor of enlargement? 0 1 2 3 4 5 6 7 8 9 10 x 1 9 8 7 6 5 4 3 2 y 10 E