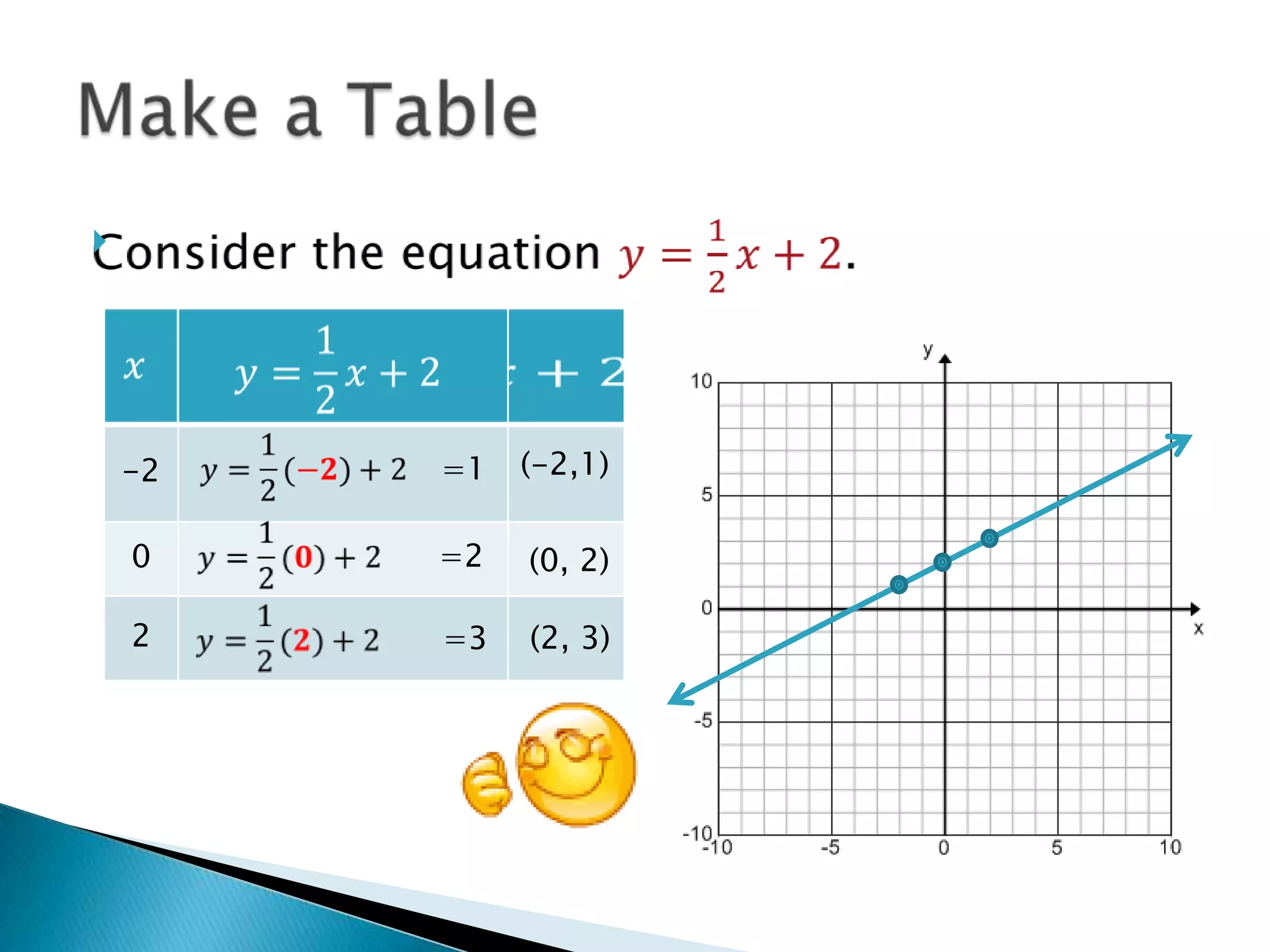
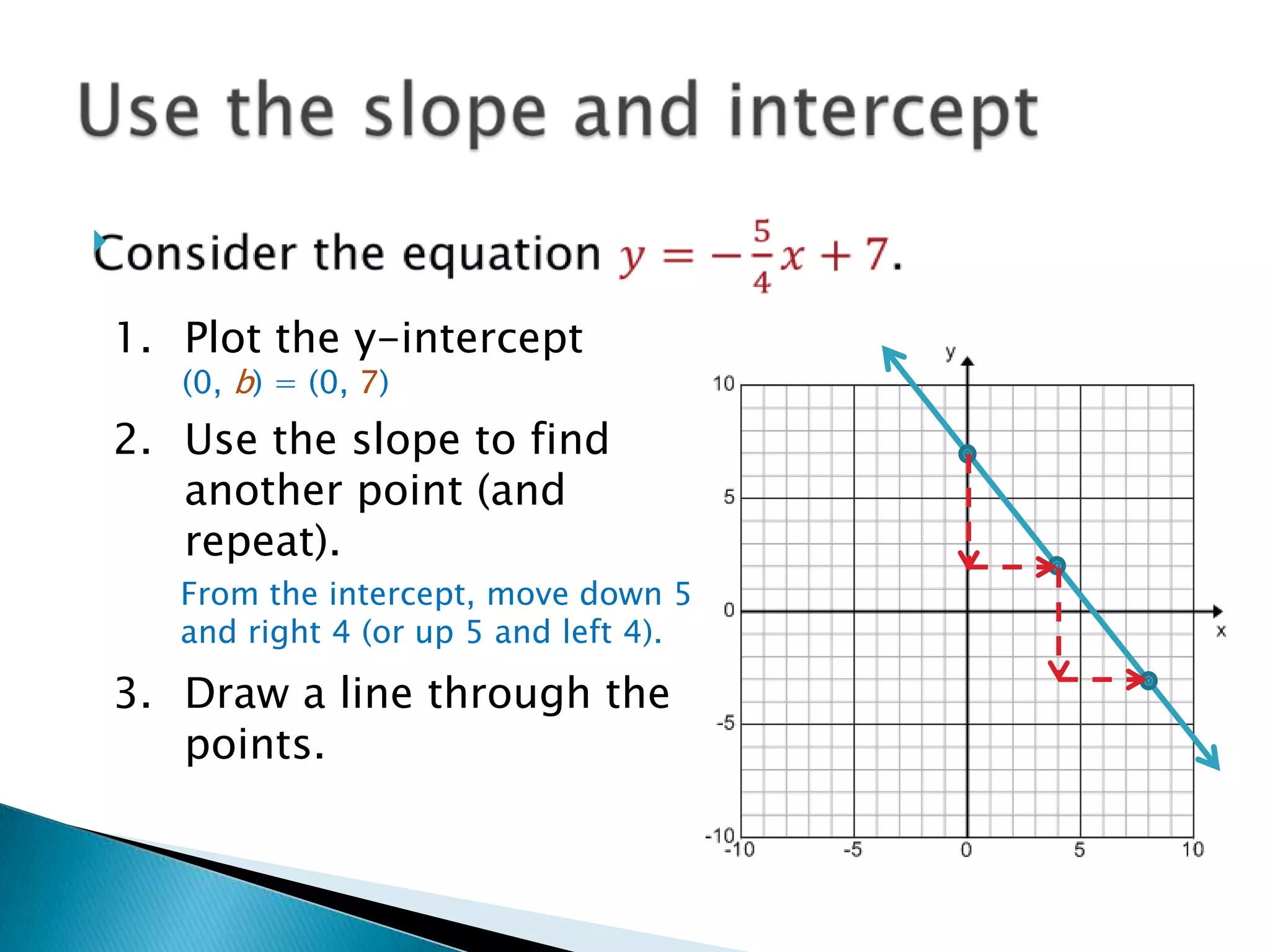
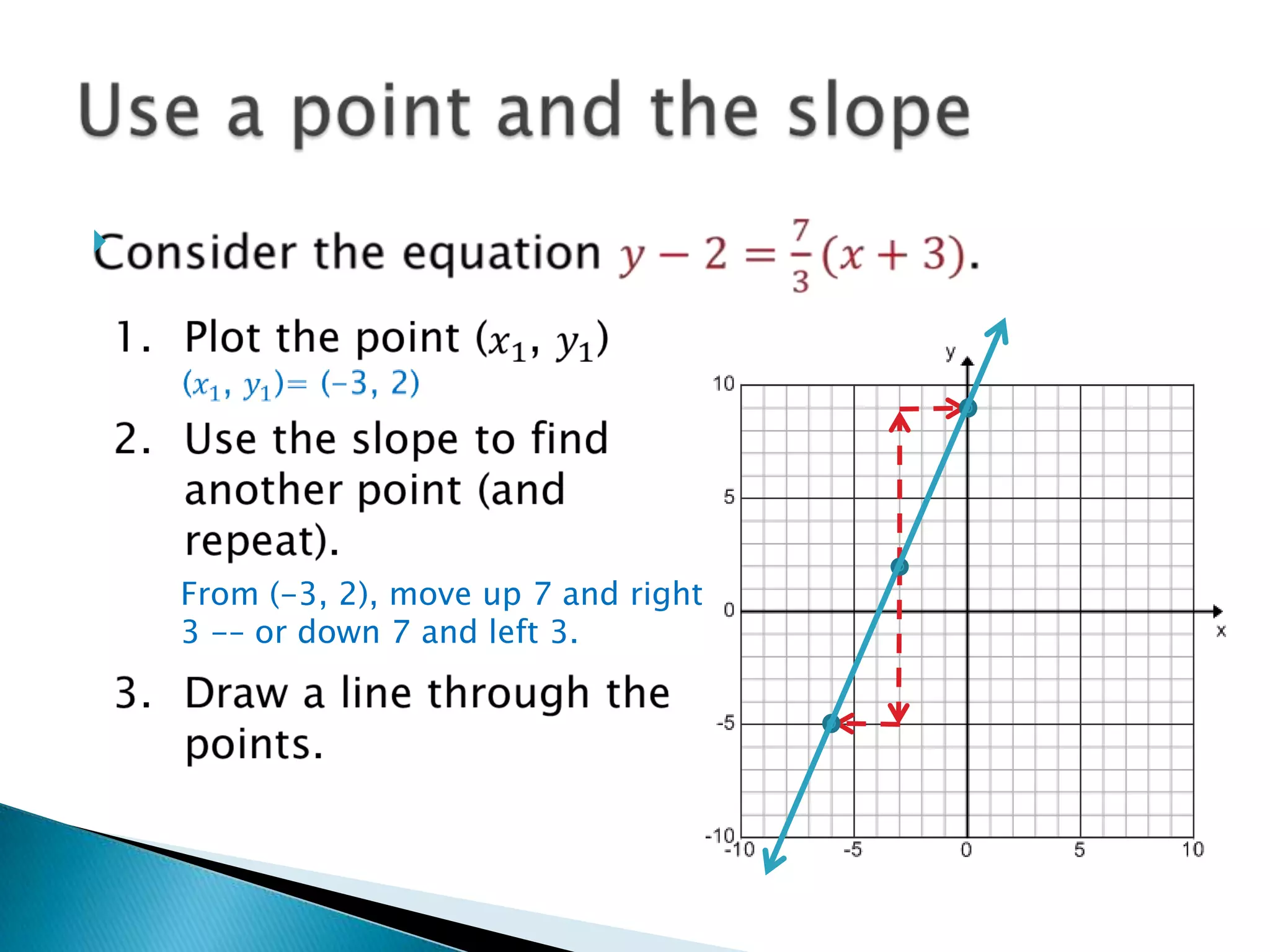
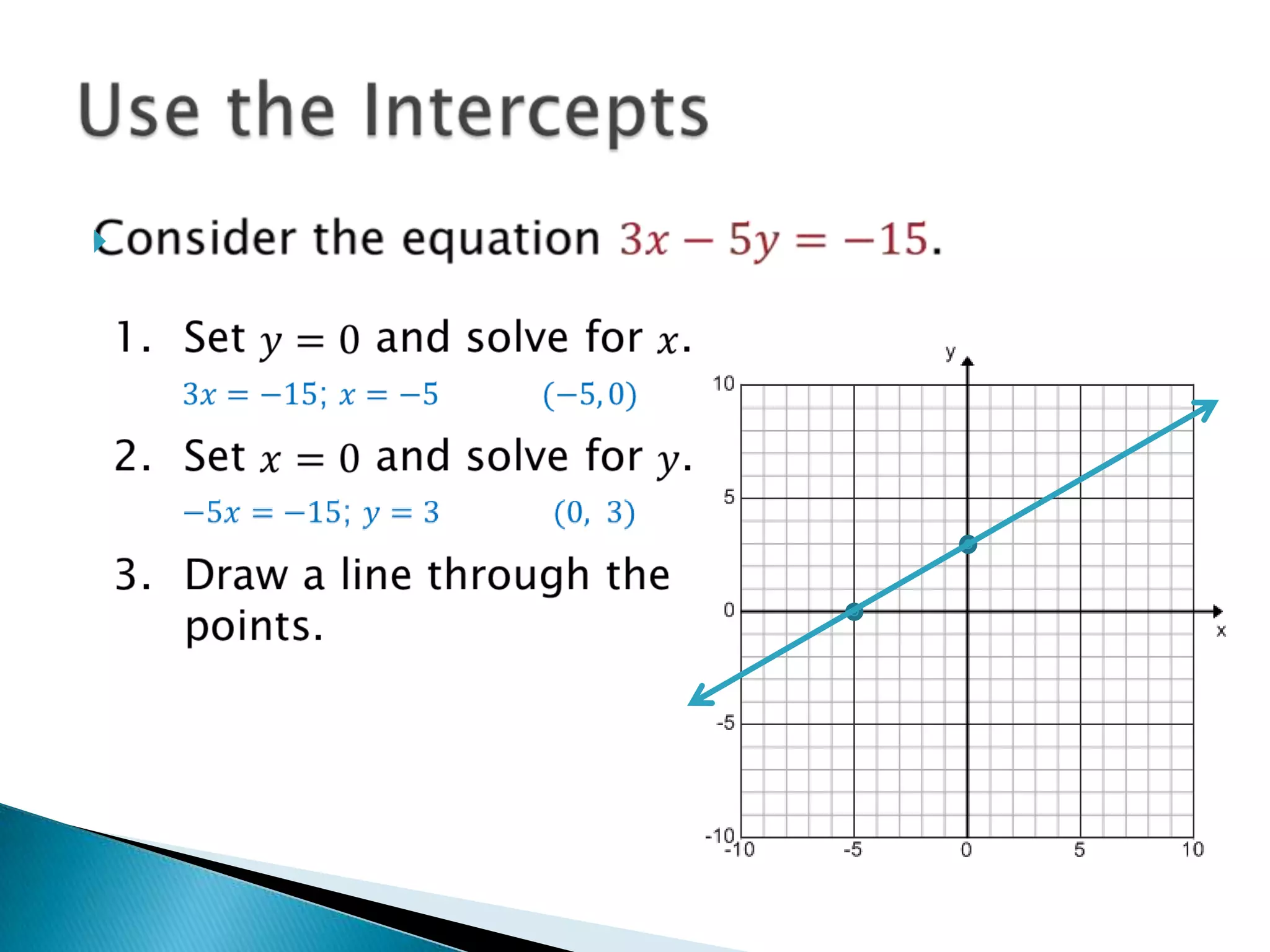
There are three main forms for writing linear equations: slope-intercept form (y=mx+b), point-slope form (y-y1=m(x-x1)), and standard form (Ax + By = C). Each form can be used to graph the line by finding ordered pairs that satisfy the equation and plotting those points. For slope-intercept form, a table of x-values with their corresponding y-values is made to find the points. For point-slope form and standard form, the given point and slope or intercepts are used to find another point which are then plotted and connected with a line.

1. Graphing Linear Equations

2. Linear Equations are most often expressed in one of three forms:Slope-Intercept Form: 𝑦=𝑚𝑥+𝑏,Point-Slope Form: 𝑦−𝑦1=𝑚(𝑥−𝑥1), andStandard Form: 𝐴𝑥+𝐵𝑦=𝐶.Each form allows for quick and easy ways to graph the line they represent. Forms of Linear Equations

3. One method for graphing a line is to use a table. This is most useful when we have an equation in slope-intercept form (𝑦=𝑚𝑥+𝑏).The steps are:Assign a value to the x-variable,Calculate the corresponding value for the y-coordinate, andRepeat.In this way, we can create a table of ordered pairs and plot them on the coordinate plane. Make a Table

4. Consider the equation 𝑦=12𝑥+2. Make a Table𝑦=12(−𝟐)+2 (-2,1)=1𝑦=12(𝟎)+2 =2(0, 2)𝑦=12(𝟐)+2 (2, 3)=3

5. Another method for graphing lines when an equation is in slope-intercept form is as follows:Plot the y-intercept on the coordinate plane; that's the point (0, b).Use the slope to find another point (and repeat).Draw a line through the points.Use the slope and intercept

6. Consider the equation𝑦=−54𝑥+7. Plot the y-intercept Use the slope to find another point (and repeat).Draw a line through the points.Use the slope and intercept(0, b) = (0, 7)From the intercept, move down 5 and right 4 (or up 5 and left 4).

7. This method is very similar to the slope-intercept method. To graph a line using this method, do the following:Plot the point (𝑥1, 𝑦1).Use the slope to find another point (and repeat).Draw a line through the points. Use a point and the slope

8. Consider the equation𝑦−2=73(𝑥+3). Plot the point (𝑥1, 𝑦1)Use the slope to find another point (and repeat).Draw a line through the points. Use a point and the slope(𝑥1, 𝑦1)= (-3, 2) From (-3, 2), move up 7 and right 3 -– or down 7 and left 3.

9. This method is used when the line is in Standard Form (𝐴𝑥+𝐵𝑦=𝐶). The x-intercept is easily calculated by setting y to 0 and solving for 𝑥.The y-intercept is calculated by setting 𝑥 to zero and solving for 𝑦.Plot the two intercepts and draw a line through them. Use the Intercepts

10. Consider the equation3𝑥−5𝑦=−15. Set 𝑦=0 and solve for 𝑥.Set 𝑥=0 and solve for 𝑦.Draw a line through the points. Use the Intercepts3𝑥=−15; 𝑥=−5(−5, 0) −5𝑥=−15; 𝑦=3(0, 3)