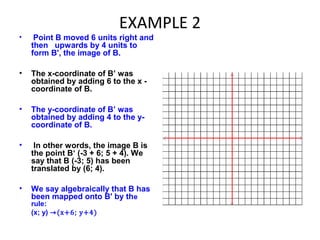
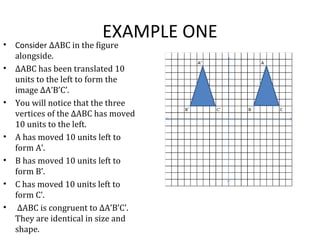
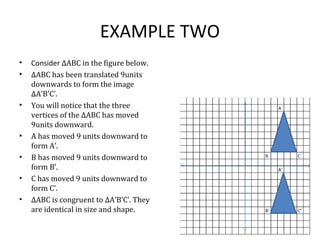
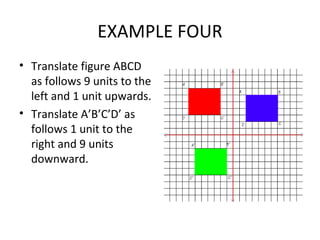
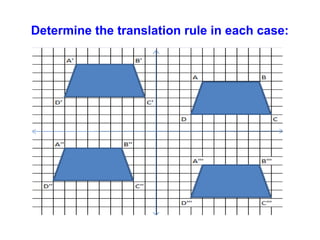
This document discusses translations in geometry. It begins by defining a translation as a horizontal or vertical slide that moves a figure without changing its shape or size. It then provides examples of translating points and figures by: 1) Translating individual points on a coordinate plane by moving them horizontally and vertically. 2) Translating triangles by moving their vertices horizontally and vertically, which demonstrates the triangle retains its shape and size. 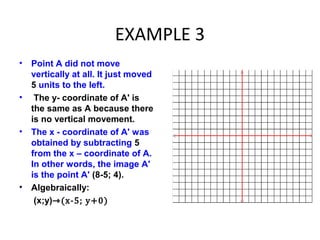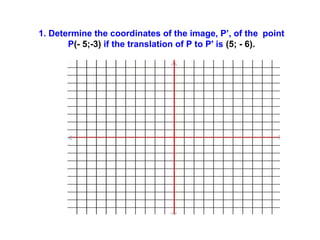3) Describing translations algebraically using notation like (x+p; y+q) to indicate a figure is translated p units horizontally and q units vertically.

1. • TARGET AUDIENCE : GRADES 7-9
• DURATION: 1 HOUR

3. Transformation geometry is the geometry of moving
points and shapes.
• The type of transformation dealt with in this
module is:
• Translations of p units horizontally and q
units vertically.
• A translation is a horizontal or vertical slide.
• The object translated does not change its
shape or size, that is the object and the
image are congruent.

4. TRANSLATION OF POINTS
• Let us first revise the
plotting of points on the
cartesian plane.
• Plot the following points on
the grid provided.
• A(2;4), B(-3;6),C(-5;-6),
• D(6;-4)
• Now translate each point 2
units to the right and 1 unit
downward.

5. EXAMPLE ONE
• Consider ∆ABC in the figure
alongside.
• ∆ABC has been translated 10
units to the left to form the
image ∆A’B’C’.
• You will notice that the three
vertices of the ∆ABC has moved
10 units to the left.
• A has moved 10 units left to
form A’.
• B has moved 10 units left to
form B’.
• C has moved 10 units left to
form C’.
• ∆ABC is congruent to ∆A’B’C’.
They are identical in size and
shape.

6. EXAMPLE TWO
• Consider ∆ABC in the figure below.
• ∆ABC has been translated 9units
downwards to form the image
∆A’B’C’.
• You will notice that the three
vertices of the ∆ABC has moved
9units downward.
• A has moved 9 units downward to
form A’.
• B has moved 9 units downward to
form B’.
• C has moved 9 units downward to
form C’.
• ∆ABC is congruent to ∆A’B’C’. They
are identical in size and shape.

7. EXAMPLE THREE
• In this example, ABC has first
translated 11 units to the left and
then 9 units downwards.
• Notice that the three vertices have
moved 11 units to the left and then
9 units downwards.
• A has moved 11 units to the left
and then 9 units downward to
form A‘
• B has moved 11 units to the left
and then 9 units downward to
form B‘
• C has moved 11 units to the left
and then 9 units downward to
form C‘
• Clearly, figure ABC is congruent to
A'B'C’ since they are identical in
size and shape.

8. EXAMPLE FOUR
• Translate figure ABCD
as follows 9 units to the
left and 1 unit upwards.
• Translate A’B’C’D’ as
follows 1 unit to the
right and 9 units
downward.

9. In each of the following
diagrams, a point has been
translated by a horizontal
move followed by a vertical
move to form its image.

10. Describe the translation and then represent the translation
in mathematical notation (algebraically).
• EXAMPLE 1
• Point A moved left by 8 units
and then downwards by 4
units to form A', the image of
A.
The x-coordinate of A' was
obtained by subtracting 8
from the x-coordinate of A.
The y-coordinate of A’ was
obtained by subtracting 4
from the y-coordinate of A.
In other words, the image A'
is the point A'(3-8; 5-4).
We say that A(3; 5) has been
translated by (-8 ; - 4).
Algebraically:
(x;y)⇾(x-8; y-4)

11. EXAMPLE 2
• Point B moved 6 units right and
then upwards by 4 units to
form B', the image of B.
• The x-coordinate of B’ was
obtained by adding 6 to the x -
coordinate of B.
• The y-coordinate of B’ was
obtained by adding 4 to the y-
coordinate of B.
• In other words, the image B is
the point B‘ (-3 + 6; 5 + 4). We
say that B (-3; 5) has been
translated by (6; 4).
• We say algebraically that B has
been mapped onto B' by the
rule:
(x; y) ⇾(x+6; y+4)

12. EXAMPLE 3
• Point A did not move
vertically at all. It just moved
5 units to the left.
• The y- coordinate of A' is
the same as A because there
is no vertical movement.
• The x - coordinate of A' was
obtained by subtracting 5
from the x – coordinate of A.
In other words, the image A'
is the point A' (8-5; 4).
• Algebraically:
(x;y)⇾(x-5; y+0)

13. To summarize:
• We translate the point (x; y) to the point
(x + p; y + q) by a translation of (p ; q)
• Where p is a horizontal move and q is a vertical move.
• If p > 0, the horizontal translation is to the right.
• If p < 0, the horizontal translation is to the left.
• If q > 0, the vertical translation is upward.
• If q < 0, the vertical translation is downward.

15. 1. Determine the coordinates of the image, P’, of the point
P(- 5;-3) if the translation of P to P' is (5; - 6).

16. 2. Represent the translation algebraically if the
point Q (5; 6) is translated to the point Q‘ (- 6; -5).

17. TRANSLATION OF A FIGURE
• Draw the image A'B'C'D' and
indicate the coordinates of
the vertices of the newly
formed figure.
• The translation here is
(7; - 10), i.e. 7 units to the
right and 10 units
downward.
• The coordinates of ABCD
are as follows: A(-1;3),
B(-6;3), C(-6;7) and D(-1;7)
• First draw ABCD.

18. Determine the translation rule in each case: