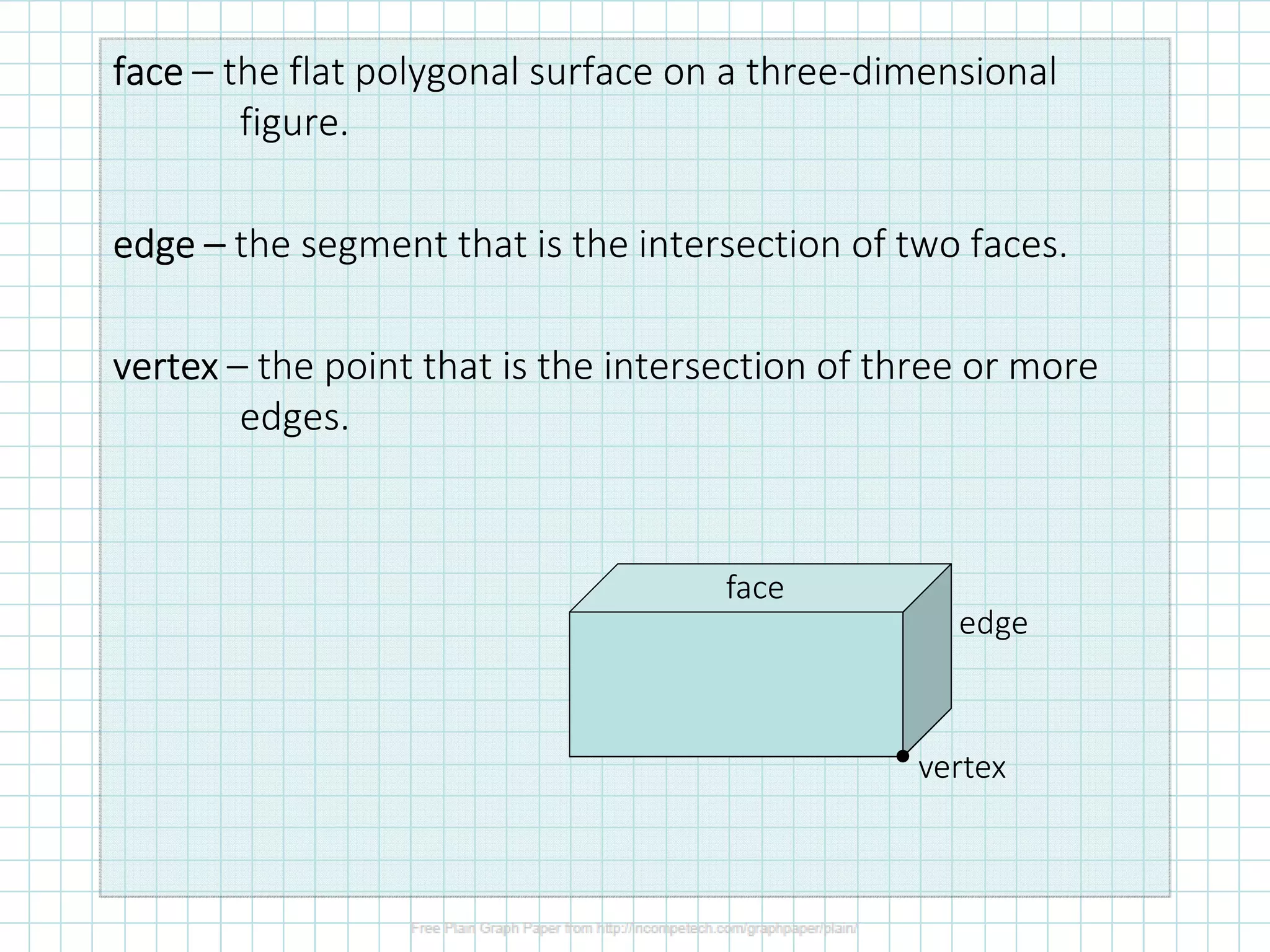
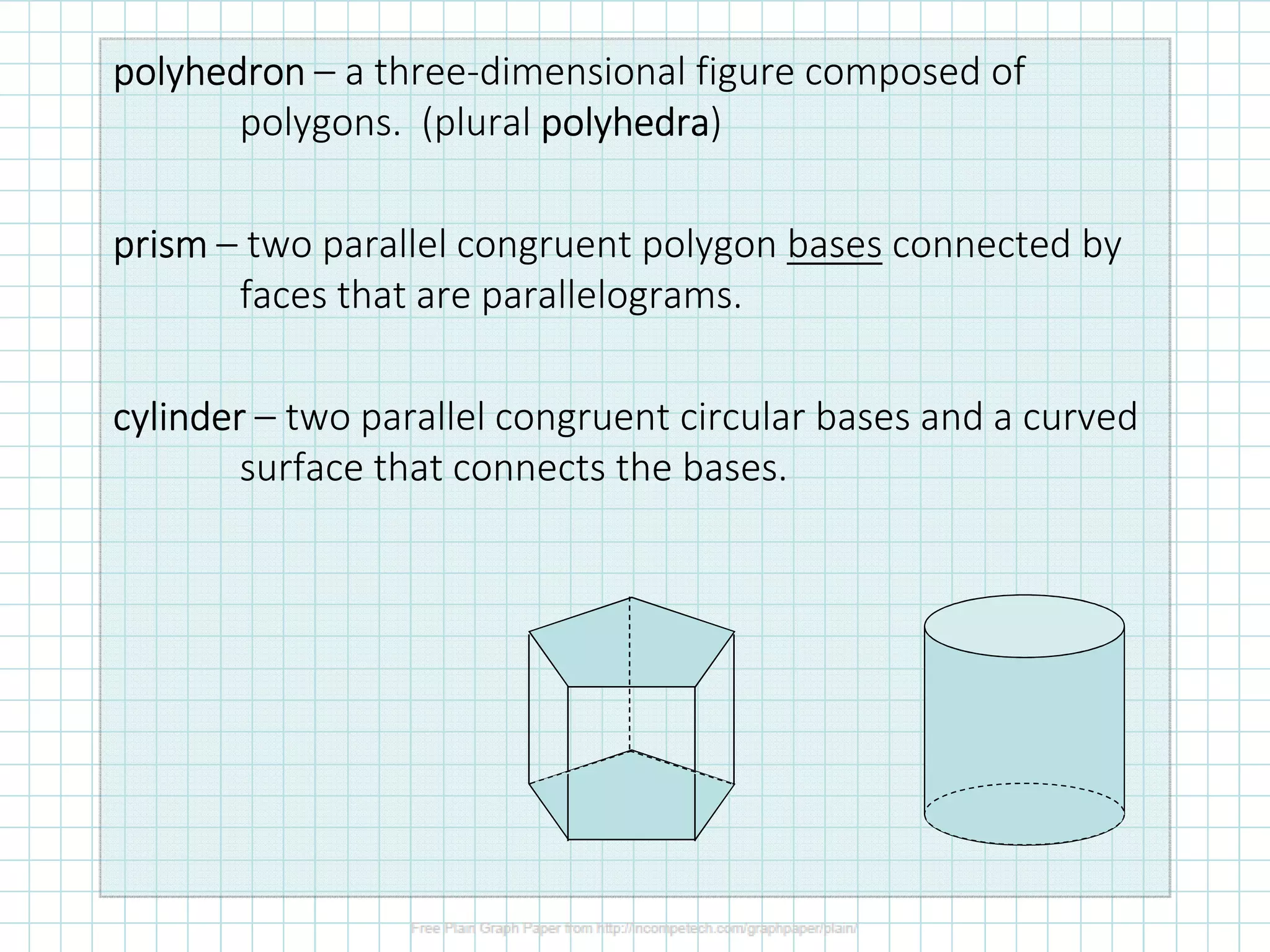
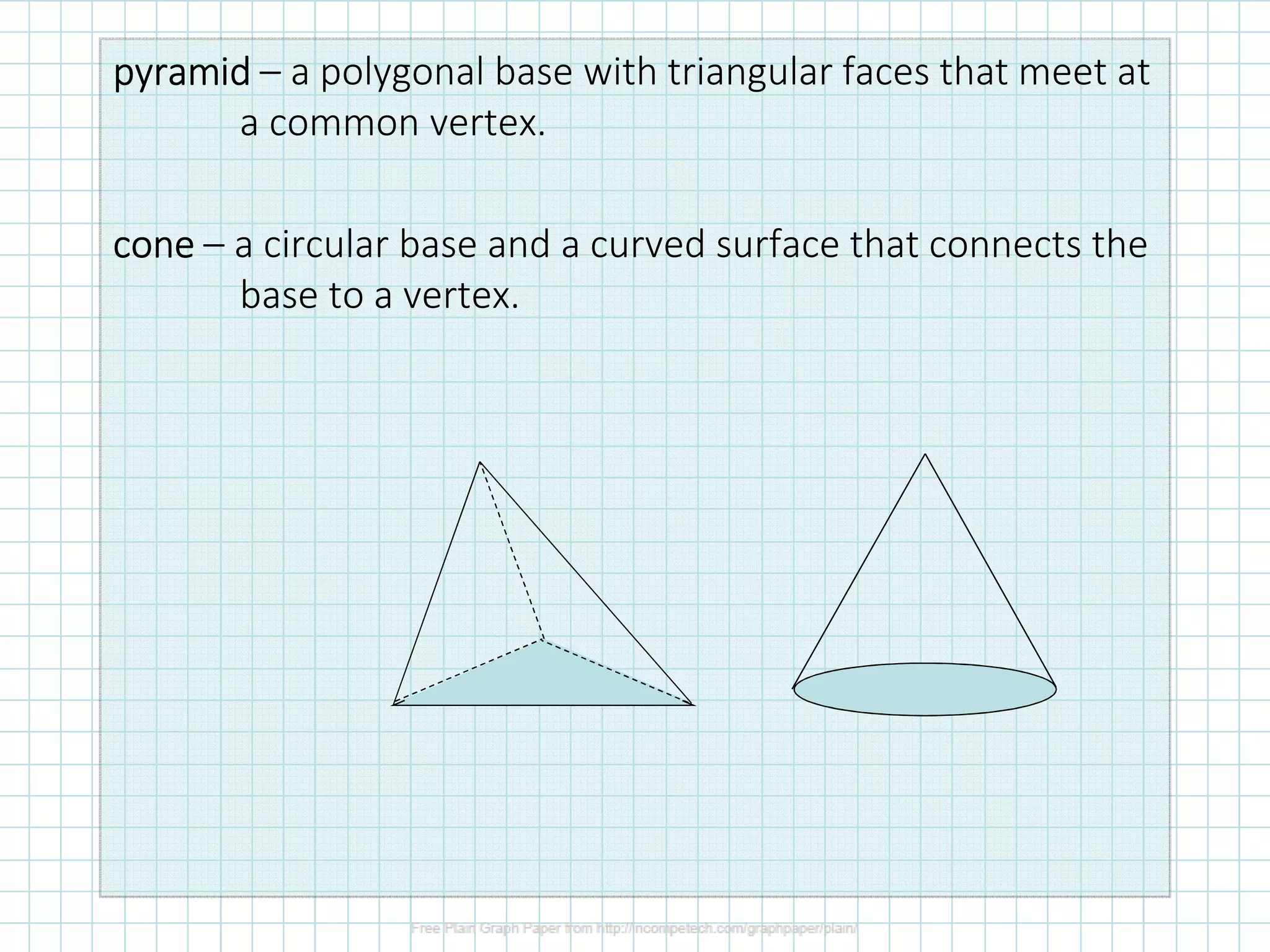
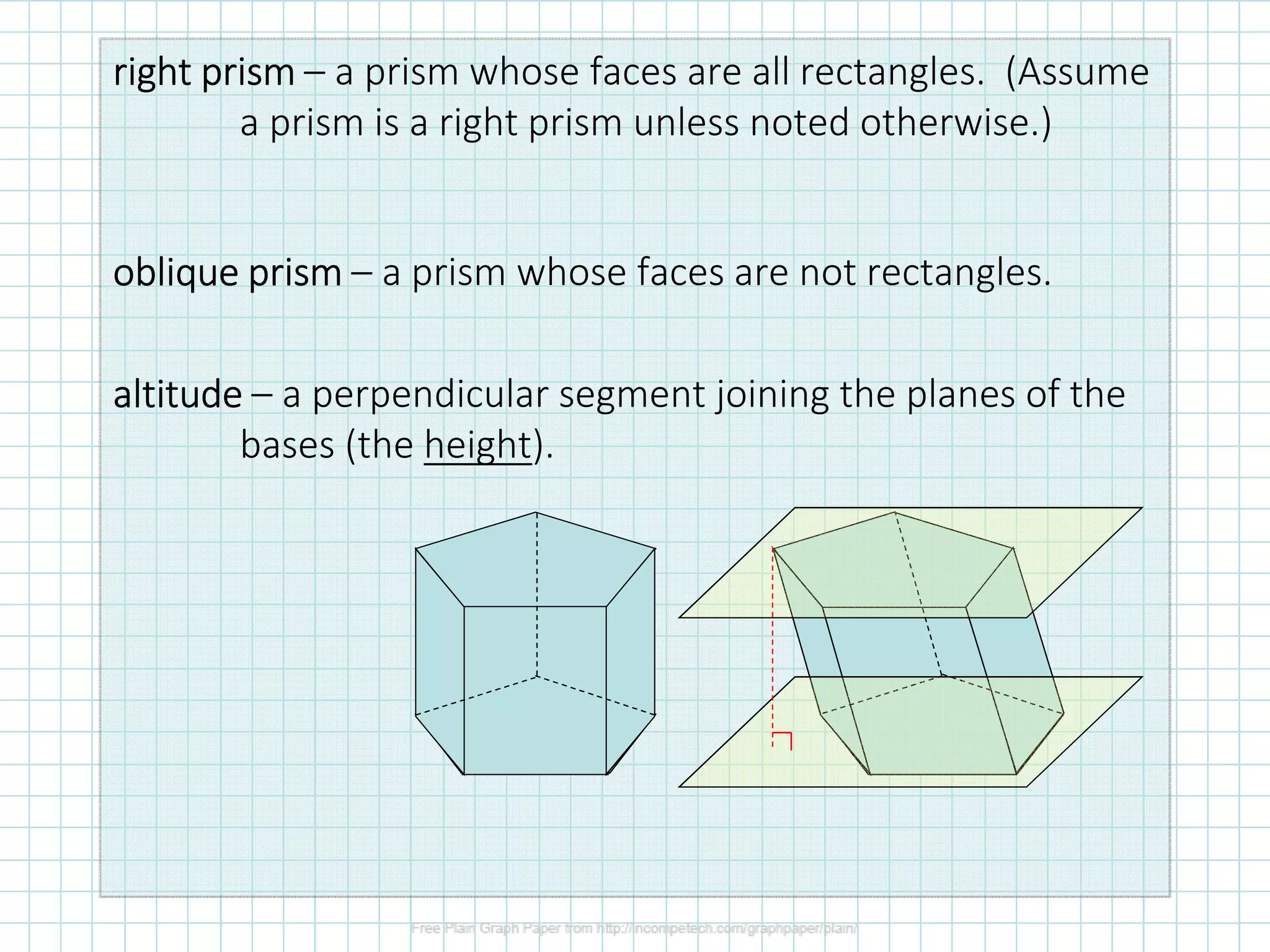
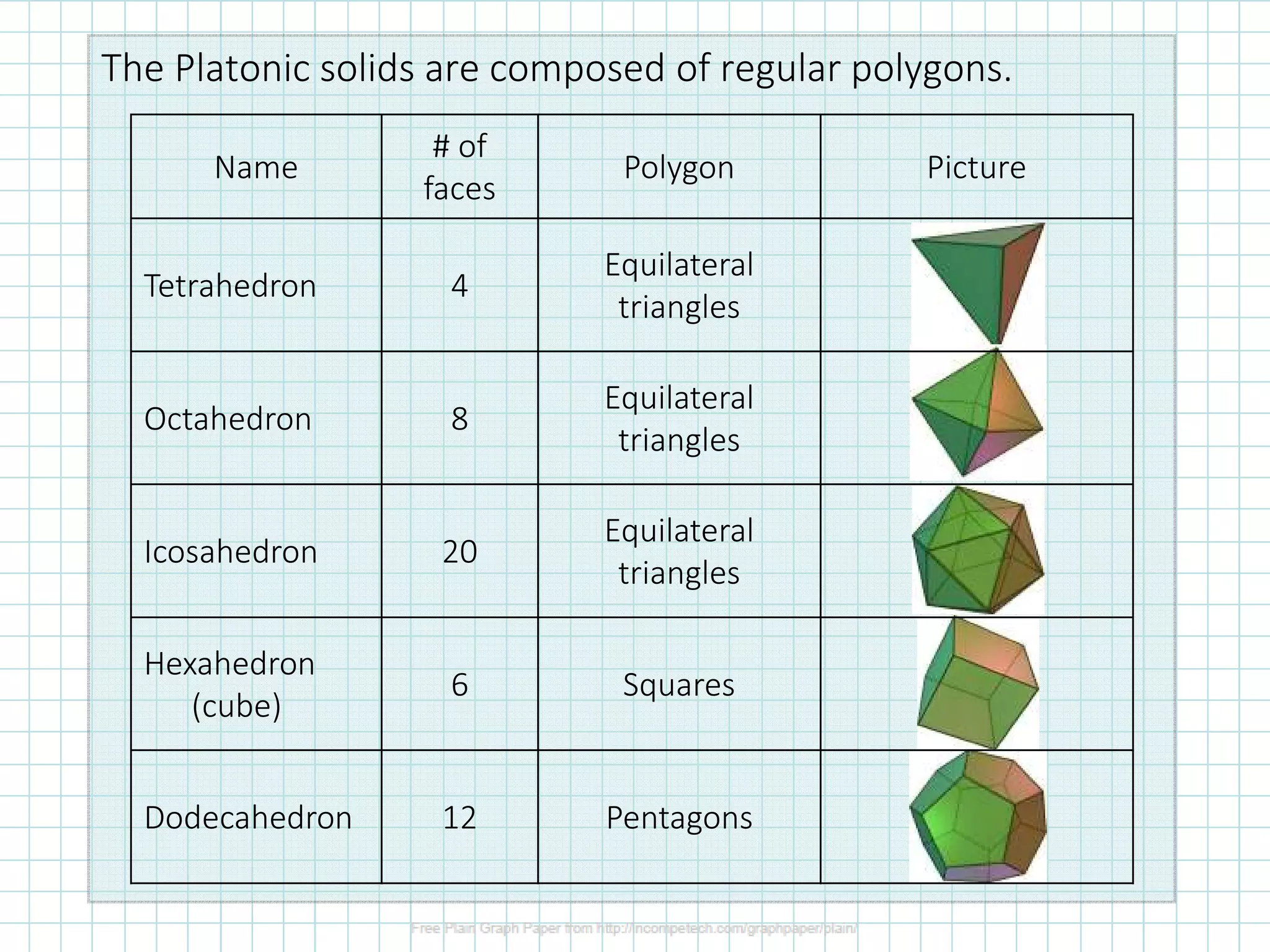
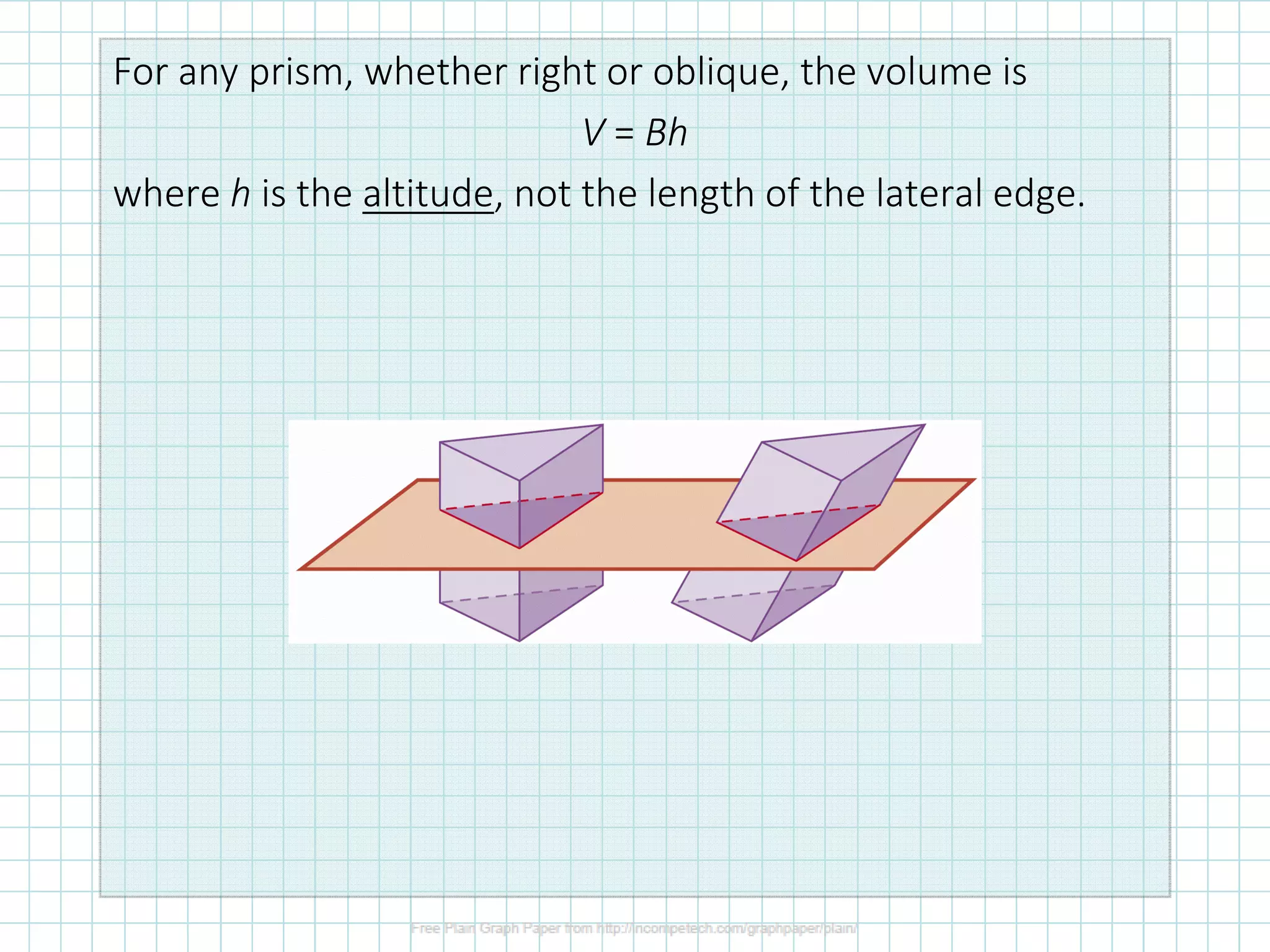
The document discusses classifying and calculating volumes of prisms and cylinders. It defines key terms like face, edge, and vertex. Prisms have two parallel congruent polygon bases connected by faces that are parallelograms, while cylinders have two parallel congruent circular bases. The volume of any prism or cylinder can be calculated as V=Bh, where B is the area of the base and h is the height or altitude. Examples calculate the volumes of different prisms and cylinders.

1. Volume of Prisms and Cylinders
The student is able to (I can):
• Classify three-dimensional figures according to their
properties
• Calculate the volumes of prisms and cylinders

2. facefacefaceface – the flat polygonal surface on a three-dimensional
figure.
edgeedgeedgeedge –––– the segment that is the intersection of two faces.
vertexvertexvertexvertex – the point that is the intersection of three or more
edges.
face
edge
vertex•

3. polyhedronpolyhedronpolyhedronpolyhedron – a three-dimensional figure composed of
polygons. (plural polyhedrapolyhedrapolyhedrapolyhedra)
prismprismprismprism – two parallel congruent polygon bases connected by
faces that are parallelograms.
cylindercylindercylindercylinder – two parallel congruent circular bases and a curved
surface that connects the bases.

4. pyramidpyramidpyramidpyramid – a polygonal base with triangular faces that meet at
a common vertex.
coneconeconecone – a circular base and a curved surface that connects the
base to a vertex.

5. rightrightrightright prismprismprismprism – a prism whose faces are all rectangles. (Assume
a prism is a right prism unless noted otherwise.)
obliqueobliqueobliqueoblique prismprismprismprism – a prism whose faces are not rectangles.
altitudealtitudealtitudealtitude – a perpendicular segment joining the planes of the
bases (the height).

6. A cubecubecubecube is a prism with six square faces. Other prisms and
pyramids are named for the shape of their bases:

7. The Platonic solids are composed of regular polygons.
Name
# of
faces
Polygon Picture
Tetrahedron 4
Equilateral
triangles
Octahedron 8
Equilateral
triangles
Icosahedron 20
Equilateral
triangles
Hexahedron
(cube)
6 Squares
Dodecahedron 12 Pentagons

8. Euler’s Formula
For any polyhedron with V vertices, E edges, and F faces:
V − E + F = 2.
Example: If a given polyhedron has 12 vertices and 18 edges,
how many faces does it have?
− + =
− + =
=
2
12 18 2
8
V E F
F
F

9. VolumeVolumeVolumeVolume
Let’s consider a deck of cards. If a deck is stacked neatly, it
resembles a right rectangular prism. The volume of the
prism is
V = Bh,
where B is the area of one card, and h is the height of the
deck.
If we shift the deck so that it becomes an
oblique prism, does it have the same
number of cards?

10. For any prism, whether right or oblique, the volume is
V = Bh
where h is the altitude, not the length of the lateral edge.

11. Likewise, for cylinders, it doesn’t matter whether the cylinder
is right or oblique, the volume is
V = Bh = πr2h

12. Examples
Find the volume of each figure:
1.
2.
10 ft.
8 ft.
3 m
19 m

13. Examples
Find the volume of each figure:
1.
2.
10 ft.
8 ft.
3 m
19 m
( )2 2
3 9 m= π = πB
3
(9 )(19) 171 mV = π = π
( )( )2
5 10
172.05
180
4tan
5
= =
 
 
 
B
V = (172)(8) = 1376 ft3