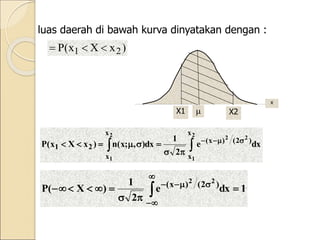
Dokumen ini membahas tentang distribusi teoritis dalam statistik, termasuk perbedaan antara distribusi teoritis dan distribusi frekwensi, serta menjelaskan berbagai jenis distribusi seperti binomial, poisson, dan normal. Penjelasan mencakup rumus-rumus dasar, aplikasi dalam percobaan, dan cara perhitungan probabilitas serta rata-rata. Selain itu, terdapat contoh penerapan distribusi dalam situasi nyata seperti pelemparan mata uang dan pelestarian energi.

1. DISTRIBUSI TEORITIS
Tita Talitha, MT

2. PENGERTIAN DISTRIBUSI
TEORITIS
 Distribusi teoritis adalah distribusi yang
frekwensinya diturunkan secara matematis.
 Pada distribusi frekwensi, frekwensinya diperoleh
dari hasil observasi/pengamatan.
 Perbedaan antara distribusi teoritis dan distribusi
frekwensi dapat dilihat pada tabel hasil observasi
pelemparan sebuah mata uang sebanyak 100 kali.

3. Sisi mata
uang
Percob.1 Percob.2 Percob.3 Percob.4
Sisi gambar 54 61 59 41
Sisi tulisan 46 39 41 59
Jumlah
percobaan
100 100 100 100

4. Kesimpulan:
 dari percobaan tersebut akan sampai pada teori
bahwa mata uang adalah setimbang, artinya
probabilita munculnya sisi gambar dan sisi tulisan
adalah sama, yaitu 50%.
 Distribusi teoritis munculnya sisi gambar dan
tulisan dari pelemparan sebuah mata uang logam
sebanyak 100 kali seperti yang terlihat pada tabel.
 Berdasarkan tabel diketahui bahwa frekwensi
teoritis diperoleh dengan mengalikan probabilita
dengan jumlah percobaan.

5. Sisi mata uang Probabilita Frekwensi
teoritis
Sisi gambar 1/2 1/2 x 100 = 50
Sisi tulisan 1/2 1/2 x 100 = 50
Jumlah 100

6. Manfaat mempelajari distribusi
teoritis
 Dengan mempelajari distribusi teoritisnya, maka
kita menjadi tahu pola distribusi frekwensinya.
 Contoh:
Pengusaha rumah makan perlu mengetahui pola
selera makan yang digemari para pelanggannya,
dengan melihat pengalaman masa lalu.
Dengan demikian pengusaha tersebut dapat
menyesuaikan persediaan barang-barangnya.

7. MACAM DISTRIBUSI
TEORITIS
Macam distribusi teoritis yaitu:
a. Distribusi Binomial
b. Distribusi Poisson
c. Distribusi Normal

8. VARIABEL DISKRIT DAN
VARIABEL KONTINYU
Variabel diskrit:
1. Variabel yang merupakan bilangan
bulat dan jumlahnya terbatas
2. Variabel yang merupakan hasil
penghitungan
Variabel kontinyu:
1. Variabel yang terdiri dari nilai-nilai yang
terletak dalam interval tertentu, bisa
berupa bilangan bulat maupun pecahan
2. Variabel yang merupakan hasil
pengukuran

9. DISTRIBUSI BINOMIAL
(Distribusi Probabilitas Diskrit)

10. Percobaan Bernoulli :
Sifat-sifat sebagai berikut :
 Percobaan itu terdiri dari n pengulangan
 Tiap pengulangan memberikan hasil yang
dapat diidentifikasi sukses atau gagal
 Probabilitas sukses dinyatakan dengan p,
tetap konstan (tidak berubah) dari satu
pengulangan ke pengulangan lainnya,
sedangkan probabilitas gagal adalah q = 1- p
 Tiap pengulangan dan pengulangan lainnya
saling bebas.

11. Distribusi Binomial
 Banyaknya X sukses dalam n pengulangan
suatu percobaan bernoulli disebut sebagai
variabel random Binomial, sedangkan
distribusi probabilitasnya disebut distribusi
Binomial dan nilainya dinyatakan sebagai :
b(x,n,p) dimana x = 1, 2, …, n
x
n
x
q
p
x
n
)
p
,
n
;
x
(
b 










12. Rata-rata dan Variansi Distribusi
Binomial:
 Rata-rata =
 Variansi =
np


npq
2


dimana : μ = rata-rata
n = jumlah percobaan
p = probabilita sukses
Deviasi standar dari distribusi binomial:
σ = √n x p (1-p)

13. DISTRIBUSI BINOMIAL
Contoh:
Sebuah mata uang dilempar sebanyak 5 kali.
Berapa probabilita munculnya sisi gambar
sebanyak 2 kali?
Jawab:
diketahui n = 5
x = 2
maka P (x,n) = nCx . px . q (n-x)
P (2,5) = 5C2 (1/2)2 x (1/2) (5-2)
= 10 x 1/4 x 1/8
= 10/32 = 5/16

14. DISTRIBUSI BINOMIAL
Contoh:
Berapa rata-rata dan deviasi standar dari
pelemparan sebuah mata uang yang dilempar 300
kali?
Jawab:
p = ½
n = 300
rata-rata (μ ) = 300 x ½
= 150
deviasi standar (σ) = √ 300 (1/2) (1/2)
= 8,66
Sehingga dalam jarak ± 2 standar deviasi, rata-rata
memperoleh sisi gambar sebanyak 150 – 2(8,66) dan 150 +
2(8,66). Atau 133 sampai 167 kali mendapatkan sisi gambar.




x

15. DISTRIBUSI POISSON
(Distribusi Probabilitas Diskrit)

16. Percobaan Poisson:
 Jika suatu percobaan menghasilkan
variabel random X yang menyatakan
banyak-nya sukses dalam daerah tertentu
atau selama interval waktu tertentu,
percobaan itu disebut percobaan Poisson.

17. Ciri-ciri distribusi poisson:
 Digunakan pada percobaan binomial jika n >50
dan P < 0,1.
 Percobaan bersifat random/acak, misalnya:
a. Kedatangan pasien di RS
b. Kedatangan mobil di POM bensin
c. Kedatangan mahasiswa di perpustakaan
d. Jumlah telepon yang masuk
 Percobaan bersifat independen
 Variabel diskrit

18. Distribusi Poisson
 Jumlah X dari keluaran yang terjadi selama
satu percobaan Poisson disebut Variabel
random Poisson, dan distribusi probabilitasnya
disebut distribusi Poisson.
 Bila x menyatakan banyaknya sukses yang
terjadi ,  adalah rata-rata banyaknya sukses
yang terjadi dalam interval waktu atau daerah
tertentu, dan e = 2,718 , maka rumus distribusi
Poisson adalah :
P(x) = (μx x e-μ ) / x !

19. Dimana: P(x) = probabilita peristiwa x
μ = rata-rata
x = jumlah sukses
e = bilangan alam = 2,7182
Rata-rata distribusi poisson:
μ = n x p

20. DISTRIBUSI POISSON
Contoh Soal:
Berdasarkan pengalaman, setiap mencetak 10.000
lembar kertas terdapat 100 lembar yang rusak.
Pada suatu waktu perusahaan mencetak 1000
lembar kertas. Hitunglah probabilitanya:
a. Tepat mendapat 5 lembar kertas yang rusak.
b. Mendapatkan paling banyak 2 lembar kertas
yang rusak.
c. Paling sedikit mendapat 2 kertas yang rusak.

21. DISTRIBUSI POISSON
Jawab:
Diketahui:
Probabilita mendapatkan kertas yang rusak
P = 100/10.000
= 0,01
μ = n x p
= 1000 x 0,01
= 10
a. P (x = 5) = (10 5 x e -10)/ 5!
= (100000 x 0,000045) / 120
= 0,0375
b. P (x ≤ 2) = P(x=0) + P(x=1) + P(x=2)

22. Hubungan Distribusi Poisson
dengan Distribusi Binomial
 Distribusi Poisson sebagai suatu bentuk
pembatasan distribusi Binomial pada saat n besar,
sedangkan p mendekati 0, dan np konstan.
 Sehingga bila n besar dan p mendekati 0, distribusi
Poisson dapat digunakan untuk memperkirakan
probabilitas Binomial, dengan  = np

23. Distribusi Normal
(Distribusi Probabilitas Kontinyu)

24. Kurva Normal dan Variabel
Random Normal
 Distribusi probabilitas kontinyu yang
terpenting adalah distribusi normal dan
grafiknya disebut kurva normal.
 Variabel random X yang distribusinya
berbentuk seperti lonceng disebut variabel
random normal.

x




25. Sifat kurva normal, yaitu :
 Kurva mencapai maksimum pada
 Kurva setangkup terhadap garis tegak
yang melalui
 Kurva mempunyai titik belok pada
 Sumbu x merupakan asimtot dari kurva
normal
 Seluruh luas di bawah kurva, di atas
sumbu x adalah 1


x


x




x

26. DISTRIBUSI NORMAL
Sifat-sifat distribusi normal :
◦ Bentuknya menyerupai lonceng dengan sebuah
puncak
◦ Nilai rata-rata (mean) pada distribusi normal akan
terletak ditengah-tengah dari kurve normal.
◦ Bentuknya simetris dengan nilai mean = median
=modus
◦ Ujung masing-masing sisi kurve sejajar dgn
sumbu horisontal dan tidak memotong sumbu
horisontal tsb.
◦ Sebagian besar data ada ditengah-tengah dan
sebagian kecil ada pada masing-masing sisi/tepi.
◦ 68% data berada dalam jarak ± 1 standar deviasi ,
95% data berada dalam jarak ± 2 standar deviasi,

27. Distribusi Normal
 Variabel random X berdistribusi
normal, dengan mean dan variansi
mempunyai fungsi densitas
)
2
(
)
x
( 2
2
e
2
1
)
,
;
x
(
n 












 x

28. luas daerah di bawah kurva dinyatakan dengan :
)
x
X
x
(
P 2
1 


X1
x














2
1
2
2
2
1
x
x
)
2
(
)
x
(
x
x
2
1 dx
e
2
1
dx
)
,
;
x
(
n
)
x
X
x
(
P
1
dx
e
2
1
)
X
(
P )
2
(
)
x
( 2
2







 







X2


29. Distribusi Normal Standar (1)
 apabila variabel X ditransformasikan
dengan substitusi
 maka :




x
Z


 









 2
1
2
1
2
2
1
2 z
z
z
z
z
2
1
z
z
z
2
1
2
1 dz
)
1
,
0
;
z
(
n
dz
e
2
1
dz
e
2
1
)
z
Z
z
(
P
ternyata substitusi




x
Z
menyebabkan distribusi normal )
,
;
z
(
n 
 menjadi
)
1
,
0
;
z
(
n , yang disebut distribusi normal standar.

30.  Karena transformasi ini, maka
selanjutnya nilai
ini dapat dihitung dengan
menggunakan tabel distribusi normal
standar.
)
x
X
x
(
P 2
1 

Distribusi Normal Standar (2):

31. Hubungan Distribusi Normal & Distribusi
Binomial:
 Jika n besar dan p atau q menuju 0, maka
distribusi binomial dapat didekati oleh
distribusi normal, sehingga bila X adalah
variabel random yang berdistribusi Binomial
dengan mean dan variansi
maka berdistribusi normal standar
np


npq
2


npq
np
X
Z



32. DISTRIBUSI NORMAL
 Contoh penggunaan kurve normal
Nilai rata-rata mata kuliah statistik dari 200 orang
mahasiswa adalah 6 dengan standar deviasi 2.
Berapa jumlah mahasiswa yang mendapat nilai 8
keatas?
jawab :
1
2
)
6
8
(
)
(





s
x
z


33. DISTRIBUSI NORMAL
 Dengan melihat tabel kurve normal dapat dilihat
bahwa luas daerah 0 sampai dengan 1 adalah
34,13 % (prosentase jumlah mahasiswa yang
nilainya 6 sampai 8)
 Jadi prosentase mahasiswa yang nilainya di atas 8
adalah 50% - 34,13% = 15,87%
 Dengan demikian jumlah mahasiswa yang nilainya
di atas 8 adalah 200 x 15,87% = 31,74 = 32 orang.

34. 6 8
34,13%
50% 15,87%
DISTRIBUSI NORMAL

35. DISTRIBUSI NORMAL
 Setelah dimulainya suatu program pelestarian
energi, PLN mencatat bahwa penghematan
penggunaan listrik yang dilakukan oleh para
pemakai di daerah tertentu rata-rata adalah 10,4
KWH setiap bulannya dengan standar deviasi 7,8
KWH. Apabila rekening untuk seseorang
pelanggan dipilih secara acak. Hitunglah
probabilitanya:
1. Penghematan listrik yang digunakan lebih dari
5 KWH
2. Penghematan listrik yang digunakan antara 5-
15 KWH.
3. Penghematan listrik yang digunakan kurang
dari 5 KWH