Distribusi Normal merupakan salah satu materi pelajaran matematika Peminatan Kelas XII Program MIPA

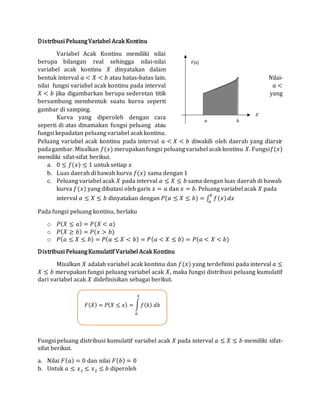
1. Distribusi PeluangVariabel Acak Kontinu
Variabel Acak Kontinu memiliki nilai
berupa bilangan real sehingga nilai-nilai
variabel acak kontinu 𝑋 dinyatakan dalam
bentuk interval 𝑎 < 𝑋 < 𝑏 atau batas-batas lain. Nilai-
nilai fungsi variabel acak kontinu pada interval 𝑎 <
𝑋 < 𝑏 jika digambarkan berupa sederetan titik yang
bersambung membentuk suatu kurva seperti
gambar di samping.
Kurva yang diperoleh dengan cara
seperti di atas dinamakan fungsi peluang atau
fungsi kepadatan peluang variabel acak kontinu.
Peluang variabel acak kontinu pada interval 𝑎 < 𝑋 < 𝑏 diwakili oleh daerah yang diarsir
padagambar. Misalkan 𝑓(𝑥) merupakanfungsi peluangvariabel acak kontinu 𝑋. Fungsi 𝑓(𝑥)
memiliki sifat-sifat berikut.
a. 0 ≤ 𝑓(𝑥) ≤ 1 untuk setiap 𝑥
b. Luas daerah di bawah kurva 𝑓(𝑥) sama dengan 1
c. Peluang variabel acak 𝑋 pada interval 𝑎 ≤ 𝑋 ≤ 𝑏 sama dengan luas daerah di bawah
kurva 𝑓(𝑥) yang dibatasi oleh garis 𝑥 = 𝑎 dan 𝑥 = 𝑏. Peluang variabel acak 𝑋 pada
interval 𝑎 ≤ 𝑋 ≤ 𝑏 dinyatakan dengan 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = ∫ 𝑓(𝑥)
𝑏
𝑎
𝑑𝑥
Pada fungsi peluang kontinu, berlaku
o 𝑃( 𝑋 ≤ 𝑎) = 𝑃(𝑋 < 𝑎)
o 𝑃( 𝑋 ≥ 𝑏) = 𝑃(𝑥 > 𝑏)
o 𝑃( 𝑎 ≤ 𝑋 ≤ 𝑏) = 𝑃( 𝑎 ≤ 𝑋 < 𝑏) = 𝑃( 𝑎 < 𝑋 ≤ 𝑏) = 𝑃(𝑎 < 𝑋 < 𝑏)
Distribusi PeluangKumulatif Variabel Acak Kontinu
Misalkan 𝑋 adalah variabel acak kontinu dan 𝑓(𝑥) yang terdefinisi pada interval 𝑎 ≤
𝑋 ≤ 𝑏 merupakan fungsi peluang variabel acak 𝑋, maka fungsi distribusi peluang kumulatif
dari variabel acak 𝑋 didefinisikan sebagai berikut.
Fungsi peluang distribusi kumulatif variabel acak 𝑋 pada interval 𝑎 ≤ 𝑋 ≤ 𝑏 memiliki sifat-
sifat berikut.
a. Nilai 𝐹( 𝑎) = 0 dan nilai 𝐹( 𝑏) = 0
b. Untuk 𝑎 ≤ 𝑥1 ≤ 𝑥2 ≤ 𝑏 diperoleh
𝐹( 𝑋) = 𝑃( 𝑋 ≤ 𝑥) = ∫ 𝑓( 𝑘) 𝑑𝑘
𝑥
𝑎

2. 1) Untuk nilai 𝐹(𝑥1) ≤ 𝐹(𝑥2)
2) Nilai 𝑃( 𝑥1 ≤ 𝑋 ≤ 𝑥2) = 𝑃( 𝑋 ≤ 𝑥2)− 𝑃( 𝑋 ≤ 𝑥1) = 𝐹( 𝑥2)− 𝐹( 𝑥1)
c. 0 ≤ 𝐹(𝑥) ≤ 1 untuk setiap 𝑥
d.
𝑑𝐹(𝑥)
𝑑𝑥
= 𝑓(𝑥)
Contoh. Variabel X dengan fungsi kepadatan peluang
𝑓( 𝑥) = {
𝑥, 𝑢𝑛𝑡𝑢𝑘 0 < 𝑥 < 2
0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
Tentukanlah
a. 𝑃(𝑥 < 1)
b. 𝑃 (1 < 𝑥 <
3
2
)
c. 𝐹(𝑥)
d. 𝑓 (
3
2
)
Jawab
a. 𝑃( 𝑥 < 1) = ∫ 𝑥
1
0
𝑑𝑥 = [
1
2
𝑥2
]
0
1
=
1
2
. 12
−
1
2
. 02
=
1
2
b. 𝑃 (1 < 𝑥 <
3
2
) = ∫ 𝑥
3
2
1
𝑑𝑥 = [
1
2
𝑥2
]
1
3
2
=
1
2
.
3
2
2
−
1
2
.12
=
9
8
−
1
2
=
5
8
c. 𝐹( 𝑥) = 𝑃( 𝑋 ≤ 𝑥) = ∫ 𝑥
𝑥
0
𝑑𝑥 = [
1
2
𝑥2
]
0
𝑥
=
1
2
𝑥2
− 0 =
1
2
𝑥2
𝐹( 𝑥) = {
0, 𝑢𝑛𝑡𝑢𝑘 𝑥 ≤ 0
1
2
𝑥2
, 𝑢𝑛𝑡𝑢𝑘 0 < 𝑥 < 2
1 𝑢𝑛𝑡𝑢𝑘 𝑥 ≥ 2
d. 𝑓 (
3
2
) =
3
2
karena 𝑓(𝑥) bukan peluang jadi nilainya bisa lebih dari 1
Contoh. Diketahui fungsi kepadatan peluang 𝑓( 𝑥) = {
1
8
𝑥, 𝑢𝑛𝑡𝑢𝑘 0 ≤ 𝑥 ≤ 4
0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
tentukan 𝐹(𝑥)
Jawab.
𝐹( 𝑥) = 𝑃( 𝑋 ≤ 𝑥) = ∫
1
4
𝑥
0
𝑥 𝑑𝑥 = [
1
8
𝑥2
]
0
𝑥
=
1
8
𝑥2
− 0 =
1
8
𝑥2

3. 𝐹( 𝑥) = {
0 𝑢𝑛𝑡𝑢𝑘 𝑥 < 0
1
8
𝑥2
𝑢𝑛𝑡𝑢𝑘 0 ≤ 𝑥 ≤ 4
1 𝑢𝑛𝑡𝑢𝑘 𝑥 > 4
Contoh. Diketahui 𝑓( 𝑥) = {
𝑎𝑥2
, 𝑢𝑛𝑡𝑢𝑘 1 < 𝑥 < 4
0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
a. Tentukan nilai 𝑎 agar 𝑓(𝑥) merupakan fungsi kepadatan peluang (fkp)
b. Untuk nilai 𝑎 yang didapat, tentukan 𝑃(2 < 𝑥 < 3)
Jawab.
a. Agar 𝑓(𝑥) merupakan fungsi kepadatan pelaung maka ∫ 𝑓( 𝑥)
∞
−∞
𝑑𝑥 = 1 → ∫ 𝑎𝑥24
1
𝑑𝑥 = 1
[
1
3
𝑎𝑥3
]
1
4
= 1
1
3
𝑎. 43
−
1
3
𝑎. 13
= 1
64𝑎
3
−
1
3
𝑎 = 1
63𝑎
3
= 1
𝑎 =
1
21
Fungsi kepadatan peluang 𝑓( 𝑥) = {
1
21
𝑥2
, 𝑢𝑛𝑡𝑢𝑘 1 < 𝑥 < 4
0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
b. 𝑃(2 < 𝑥 < 3) = ∫
1
21
𝑥23
2
𝑑𝑥 = [
1
63
𝑥3
]
2
3
=
1
63
. 33
−
1
63
. 23
=
27
63
−
8
63
=
19
63
Distribusi kemiringan
Sebuah kurva atau histogram yang tidak simetris melambangkan kemiringan
distribusi. Misalnya, distribusi untuk kurva yang tinggi di kiri dan memiliki ekor ke kanan
dikatakan miring positif (positively skewed). Demikian pula, distribusi untuk kurva yang
tinggi di sebelahkanan danmemiliki ekorke kiri adalah dikatakan miring negatif (negatively
skewed).

4. Dalam distribusi positif miring, ekor panjang berada di arah positif. Ini kadang-
kadang dikatakan miring ke kanan. Dalam distribusi miring negatif, ekor panjang berada di
arah negatif. Ini kadang-kadang dikatakan miring ke kiri.
Contoh. Klasifikasikan Distribusi Data
Tentukan apakah data {14, 15, 11, 13, 13, 14, 15, 14, 12, 13, 14, 15} kurvanya miring positif,
miring negatif, atau berdistribusi normal.
Jawab.
Buat tabel frekuensi untuk data. Kemudian gunakan tabel untuk membuat histogram.
Karena histogram tinggi di sebelah kanan dan memiliki ekor ke kiri, datanya miring negatif.
Fungsi Peluang Variabel Acak Berdistribusi Normal
Perhatikan kurva pada gambar di samping, kuva
berbentuklonceng(genta)dansimetris terhadap 𝑥 =
𝜇. Kurva di atas sumbu 𝑋 dan mendekati sumbu 𝑋.
Variabel acak yang memiliki distribusi peluang
seperti gambar tersebut dinamakan variabel acak
normal. Fungsi peluang variabel acak normal
bergantung pada nilai rata-rata 𝜇 dan simpangan
baku 𝜎. Variabel acak 𝑋 yng memiliki peluang
berdistibusi normal dilambangkan dengan

5. 𝑋~𝑁( 𝜇, 𝜎), dibaca 𝑋 berdistribusi normaldenganrata-rata 𝜇 dansimpangan baku 𝜎. Fungsi
peluang variabel acak 𝑋~𝑁( 𝜇, 𝜎) didefinisikan sebagai berikut.
Dari kurva variabel acak 𝑋~𝑁( 𝜇, 𝜎) diperoleh sifat-sifat distribusi normal sebagai berikut.
a. Kurva selalu di atas sumbu X dan simetris terhadap garis 𝑥 = 𝜇
b. Median = modus = nilai rata-rata 𝜇
c. Untuk 𝑥 → ±∞kurvamendekati sumbu 𝑋 sehinggakurva memiliki asimtot sumbu X atau
y=0
d. Luas daerah di bawah kurva sama dengan 1
e. Peluag variabel acak 𝑋~𝑁( 𝜇, 𝜎) pada interval 𝑎 < 𝑋 < 𝑏 sama dengan luas daerah di
bawah kurva 𝑓(𝑥) yang dibatasi oleh garis 𝑥 = 𝑎 dan 𝑥 = 𝑏.
Peluang variabel acak 𝑋~𝑁( 𝜇, 𝜎) pada interval 𝑎 < 𝑋 < 𝑏 dinyatakan dengan
𝑃( 𝑎 < 𝑋 < 𝑏) =
1
𝜎√2𝜋
∫ 𝑒
−
1
2
(
𝑥−𝜇
𝜎
)
2𝑏
𝑎
𝑑𝑥
Bentuk kurva ditentukan oleh nilai rata-rata 𝜇 dan simpangan baku 𝜎. Nilai rata-rata
menentukan letak simetri suatu kurva, sedangkan simpangan baku menunjukkan seberapa
jauh data tersebut tersebar.
a. Rata-rata sama, simpangan baku berbeda
b. Rata-rata berbeda, simpangan baku sama
c. Rata-rata berbeda, simpangan baku berbeda
𝑓( 𝑥) = 𝑃( 𝑋 = 𝑥) =
1
𝜎√2𝜋
𝑒
−
1
2
(
𝑥−𝜇
𝜎
)
2
𝑢𝑛𝑡𝑢𝑘 − ∞ < 𝑥 < ∞

6. Perhatikan pula gambar berikut, gambar A dan B memiliki nilai rata-rata yang sama
dan simpangan baku berbeda, sedangkan gambar B dan C simpangan baku sama
tetapi nilai rata-rata berbeda.
Contoh. Perhatikan gambar berikut.
a. Manakah yang lebih besar rataan A atau B
b. Manakah yang lebih besar simpangan baku A atau B
jawab.
a. Garis simetri A adalah 15 dan garis simetri B adalah 12. Jadi nilai rata-rata A
lebih besar daripada nilai rata-rata B
b. Kurva B lebih memanjang dari kurva A, maka simpangan baku B lebih besar dari
A
Aturan Empiris

7. Bentuk kurva yang tidak memiliki kriteria di atas dikatakan memiliki distribusi tidak
simetris (distribusi menceng ke kiri atau menceng ke kanan). Fungsi kepadatan peluang
kurva normal di atas cukup rumit, maka untuk menghitung nilai peluang digunakan aturan
empiris yaitu dengan pendekatan luas yang membagi kurva normal menjadi tiga persentase
yaitu 68%, 95% dan 99,7% sehingga dikenal juga dengan aturan 68-95-99,7. Luas daerah di
bawah kurva sama dengan 1, tetapi jika dihitung luas daerah yang diarsir pada gambar di
samping diperoleh:
 Sekitar 68% dari hasil pengamatan terjadi dalam jangkauan ( 𝜇 − 𝜎) sampai ( 𝜇 + 𝜎)
 Sekitar 95% dari hasil pengamatan terjadi dalam jangkauan ( 𝜇 − 2𝜎) sampai ( 𝜇 + 2𝜎)
 Sekitar 99,7% dari hasil pengamatan terjadi dalam jangkauan ( 𝜇 − 3𝜎) sampai ( 𝜇 + 3𝜎)
Jika dibagi menjadi 6 bagian diperoleh kurva berikut
Latihan. Pak Adam memberi ujian 30 siswa materi Aljabar 2 di akhir semester pertama.
Skor itu terdistribusi secara normal dengan skor rata-rata 78 dan simpangan baku 6.
a. Berapa persen dari kelas yang akan Anda harapkan memiliki skor antara 72 dan 84?
b. Berapa persen dari kelas yang akan Anda berharap mendapat nilai antara 90 dan 96?
c. Kira-kira berapa banyak siswa memperoleh skor antara 84 dan 90?
Jawab.
a. Selisih dengan simpangan baku

8. 𝑏𝑎𝑤𝑎ℎ:
(72−78)
6
= −
6
6
= 1 dan 𝑎𝑡𝑎𝑠:
(84−78)
6
=
6
6
= 1
Koefisin dari 𝜎 adalah -1 dan 1
Hasil pengamatan terjadi dalam jangkauan ( 𝜇 − 𝜎) sampai ( 𝜇 + 𝜎)
Dari daerah luas daerah yang diarsir pada gambar sekitar 68%
Jadi skor antara 72 dan 84 adalah 68,4%
b. Selisih dengan simpangan baku
𝑏𝑎𝑤𝑎ℎ:
(90−78)
6
=
12
6
= 2 dan 𝑎𝑡𝑎𝑠:
(96−78)
6
=
18
6
= 3
Koefisin dari 𝜎 adalah +2 dan +3
Hasil pengamatan terjadi dalam jangkauan ( 𝜇 + 2𝜎) sampai ( 𝜇 + 3𝜎)
Dari daerah luas daerah yang diarsir pada gambar sekitar 2,15%
Jadi skor antara 72 dan 84 adalah 2,15%
c. Selisih dengan simpangan baku
𝑏𝑎𝑤𝑎ℎ:
(84−78)
6
=
6
6
= 1 dan atas
(90−78)
6
=
12
6
= 2
Koefisien dari 𝜎 adalah +1 dan +2
Persentase skor adalah 13,6%
Banyak siswa = 13,6% × 1.800 = 244,8 = 245 siswa
Distribusi Normal Baku
Jika nilai 𝜇 = 0 dan 𝜎 = 1, diperoleh distribusi
normal baku (standar). Variabel acak Z berdistribusi
normal baku dengan 𝑍~𝑁(0,1). Fungsi peluang
variabel acak 𝑍~𝑁(0,1) didefinisikan sebagai
𝑓( 𝑧) = 𝑃( 𝑍 = 𝑧) =
1
√2𝜋
𝑒
−
1
2
𝑧2
𝑢𝑛𝑡𝑢𝑘 − ∞ < 𝑧 < ∞
Kurva variabel acak 𝑍~𝑁(0,1) seperti gambar di atas.
Fungsi distributif kumulatif variabel acak 𝑍~𝑁(0,1) didefinisikan sebagai
Dengan mentransformasikan variabel acak X, di mana absis pada garis simetrinya
adalah 𝑋 = 𝜇 dari distribusi normal ke variabel Z dengan absis pada garis simterinya adalah
𝑋 = 0, diperolehdistribusi normal baku (distribusi normalstandar). Grafik distibusi normal
baku dengan absis sumbu simetri 𝑍 = 0 (berkaitan dengan 𝑋 = 𝜇 pada grafik distibusi
𝐹( 𝑧) = 𝑃( 𝑍 ≤ 𝑧) = ∫ 𝑓( 𝑧) 𝑑𝑧
𝑧
−∞
=
1
√2𝜋
∫ 𝑒−
1
2
𝑧2
𝑧
−∞
𝑑𝑧

9. normal) serta berturut-turut 𝑍 = ±1, 𝑍 = ±2 dan 𝑍 = ±3, yang berkaitan dengan 𝑋 = 𝜇 ±
𝜎, 𝑋 = 𝑋 = 𝜇 ± 2𝜎, dan 𝑋 = 𝜇 ± 3𝜎, ditunjukkan pada gambar berikut.
Transformasi dari distribusi normal dengan variabel acak 𝑋̅ = 𝜇, simpangan baku 𝜎 ke
distribusi normal baku yang telah dibuatkan tabelnya dengan variabel 𝑍 dan rata-ratanya
telah ditransformasikan ke 0 dengan menggunakan persamaan:
Bentuk di atas biasa disebut skor Z. Penting mengetahui perbedaan antara x dan z. Variabel
acak x disebut skormentah danmewakili nilai dalam ditribusi normaltidak baku, sedangkan
z mewakili nilai dalam distribusi normal baku.
Contoh. Berat badan siswa mempunyai distribusi normal dengan rata-rata = 60 dan deviasi
standar = 10. Tentukan nilai variabel normal baku bagi siswa yang memiliki berat badan 50
dan 70 !
Jawab.
Diketahui 𝜇 = 60 dan 𝜎 = 10
Untuk berat badan 50 diperoleh 𝑍 =
50−60
10
=
−10
10
= −1
Untuk berat badan 70 diperoleh 𝑍 =
70−60
10
=
10
10
= +1
MenentukanPeluang Variabel Acak
Jika variabel acak X telah ditrasnformasikan ke dalam variabel Z maka peluang dapat
dihitung dengan menentukan bagian-bagian luas dari distribusi normal baku dengan
menggunakan tabel distribusi normal baku. Cara menentukan bagian-bagian luas dari
distribusi simpangan baku sebagai berikut.
𝑍 =
𝑋 − 𝜇
𝜎

10. 1. Hitung persamaan Z dengan menggunakan rumus transformasi sampai dua tempat
desimal
2. Gambarkan kurvanya
3. Letakkan nilai Z pada sumbu horizontal, tarik garis vertikal sampai memotong kurva
4. Luas yang tertera dalam tabel distribsui normal adalah luas daerah antara garis
vertikal pada langkah 3 dengan garis vertikal yang ditarik dari titik nol
5. Dalam tabel, cari tempat nilai Z pada kolom paling kiri hingga cocok sampai satu
desimal sedangkan desimal keduanya dicari pada baris paling atas
6. Dari Z kolom kiri tarik garis horizontal ke kanan dan dari Z di baris atas tarik garis
vertikal ke bawah, maka pertemuan garis horizontal dan garis vertikal menunjukkan
bilangan yang luasnya dicari
7. Bilangan yang didapat harus ditulis dalam bentuk 0,xxxx (pecahan dalam bentuk
empat desimal). Karena luas total kurva = 1 dan kurva simetris terhadap garis
vertikal yang melalui Z=0, maka luas bagian di sisi kiri Z=0 sama dengan luas bagian
di sisi kanan Z=0, yaitu 0,5
Pada distribusi Z berlaku
 𝑃( 𝑍 ≤ 𝑧) = 𝑃( 𝑍 < 𝑧)
 𝑃( 𝑍 ≥ 𝑧) = 𝑃( 𝑍 > 𝑧)
Ada tujuh bentuk berbeda dari pernyataan peluang (probabilitas) yang mungkin kita
perlukan untuk menyelesaikan model distribusi normal baku, semuanya bisa diselesaikan
dengan bekerja mengguanakan tabel distribusi normal baku
Bentuk 1: 𝑷( 𝒁 < 𝒂) = 𝑷( 𝒁 ≤ 𝒂) dengan a bilanganpositif
Contoh. Jika 𝑍~𝑁(0,1) maka tentukan 𝑃( 𝑍 ≤ 0,23)
Jawab.
𝑍~𝑁(0,1) dibaca 𝑍 berdistibusi normal dengan 𝜇 = 0 dan 𝜎 = 1
Yang ditanyakan adalah peluang 𝑍 kurang dari 0,23 atau 𝑃( 𝑍 ≤ 0,23). Tanda ≤ atau <
sama saja

11. Kita akan cari 0,2 pada kolom paling kiri dan angka 3
pada baris atas hingga diperoleh bilangan 0,0910. Ini
berarti 𝑃(0 < 𝑍 < 0,23) = 0,0910
Luas kurva di samping
𝑃( 𝑍 ≤ 0,23) = 0,5 + 𝑃(0 < 𝑍 < 0,23) = 0,5 + 0,0910 = 0,5910
Bentuk 2: 𝑷( 𝒁 > 𝒂) = 𝑷( 𝒁 ≥ 𝒂) dengan a bilanganpositif
Contoh. Jika 𝑍~𝑁(0,1) maka tentukan 𝑃( 𝑍 > 1,23)
Jawab.
Kita akan cari 1,2 pada kolom paling kiri dan
angka 3 pada baris atas hingga diperoleh
bilangan 0,3907. Ini berarti 𝑃(0 < 𝑍 <
1,23) = 0,3907
Luas kurva di samping
𝑃( 𝑍 > 1,23) = 0,5 − 𝑃(0 < 𝑍 < 1,23)
= 0,5 − 0,3907 = 0,1093
Bentuk 3: 𝑷( 𝒁 < 𝒂) = 𝑷( 𝒁 ≤ 𝒂) dengan a bilangannegatif
Contoh. tentukanlah nilai peluang 𝑃( 𝑍 < −0,7)
Jawab.
Yang ditanya adalah 𝑃( 𝑍 < −0,7). Tetapi tabel hanya tersedia 𝑃(0 < 𝑍 < 0,7) untuk 𝑧 > 0.
Dari gambar terlihat 𝑃( 𝑍 < −0,7) = 𝑃(𝑍 > 0,7), Karena berlaku sifat simetri
Kita cari bilangan 0,7 pada kolom paling kiri dan angka 0 pada baris paling atas hingga
diperoleh bilangan 0,2580.

12. Ini berarti 𝑃(0 < 𝑍 < 0,7) = 0,2580
Lihat kurva di samping
𝑃( 𝑧 < −0,7) = 0,5 − 𝑃(0 < 𝑍 < 0,7) = 0,5 − 0,2580 = 0,2420
Bentuk 4: 𝑷( 𝒁 ≥ 𝒂) = 𝑷( 𝒁 > 𝒂) dengan a bilangannegatif
Contoh. Tentukan 𝑃( 𝑍 ≥ −1,28)
Jawab.
𝑃(−1,28 ≤ 𝑍 ≤ 0) = 𝑃(0 ≤ 𝑍 ≤ 1,28)
Kita cari bilangan 1,2 pada kolom paling kiri dan
angka 8 pada baris paling atas hingga diperoleh
bilangan 0,3997
Lihat kurva di samping
𝑃( 𝑍 ≥ −1,28) = 𝑃(−1,28 < 𝑍 < 0) + 0,5
= 𝑃(0 < 𝑍 < 1,28) + 0,5
= 0,3977 + 0,5
= 0,8977
Bentuk 5: 𝑷( 𝒂 ≤ 𝒁 ≤ 𝒃) = 𝑷( 𝒂 < 𝒁 < 𝒃)dengan a bilangannegatif, dan b bilangan positif
Contoh. Tentukan peluang 𝑃(−0,42 < 𝑍 < 1,27)
Jawab.
Dari gambar terlihat daerah yang diarsir dapat dibagi dua menjadi 𝑃(−0,42 < 𝑍 < 0) dan
𝑃(0 < 𝑍 < 1,27)
Pertama kita tentukan 𝑃(−0,42 < 𝑍 < 0), nilainya sama saja dengan 𝑃(0 < 𝑍 < 0,42). Kita
cari bilangan 0,4 pada kolom paling kiri dan angka 2 pada baris paling atas hingga
diperoleh bilangan 0,1628
Selanjutnya tentukan nilai 𝑃(0 < 𝑍 <
1,27) Kita cari bilangan 1,2 pada kolom paling
kiri dan angka 7 pada baris paling atas
hingga diperoleh bilangan 0,3980
Lihat kurva di samping
𝑃(−0,42 < 𝑍 < 1,27) = 𝑃(−0,42 < 𝑍 < 0) + 𝑃(0 < 𝑍 < 1,27)
𝑃(−0,42 < 𝑍 < 1,27) = 𝑃(0 < 𝑍 < 0,42) + 𝑃(0 < 𝑍 < 1,27)
= 0,1628 + 0,3980

13. = 0,5608
Bentuk 6: 𝑷( 𝒂 ≤ 𝒁 ≤ 𝒃) = 𝑷( 𝒂 < 𝒁 < 𝒃)dengan a bilangannegatif, dan b bilangan negatif
Contoh. Tentukan peluang dari 𝑃(−1,2 < 𝑍 < −0,5)
zawab.
Pertama tentukan nilai 𝑃(−,12 < 𝑍 < 0) =
𝑃(0 < 𝑍 < 1,2) = 0,3849
Kemudian tentukan nilai 𝑃(−0,5 < 𝑍 < 0) =
𝑃(0 < 𝑍 < 0,5) = 0,1915
𝑃(−1,2 < 𝑍 < −0,5)
= 𝑃(−,12 < 𝑍 < 0) − 𝑃(−0,5 < 𝑍 < 0)
= 0,3849 − 0,1915 = 0,1934
Bentuk 7: 𝑷( 𝒂 ≤ 𝒁 ≤ 𝒃) = 𝑷( 𝒂 < 𝒁 < 𝒃)dengan a bilanganpositif, dan b bilangan positif
Contoh. Tentukan 𝑃(0,81 < 𝑍 < 1,94)
Jawab.
Pertama tentukan nilai 𝑃(0 < 𝑍 < 1,94) = 0,4738
Kemudian nilai 𝑃(0 < 𝑍 < 0,81) = 0,2910
Sehingga nilai 𝑃(0,81 < 𝑍 < 1,94) = 𝑃(0 < 𝑍 <
1,94) − 𝑃(0 < 𝑍 < 0,81)
= 0,4738 − 0,2910
= 0,1828
PenerapanDistibusi Normal Baku
Contoh. Rata-rata berat sebuah kotak adalah 283 gram dan simpangan baku 1,6 gram.
Berapakah probabilitas sebuah kotak dibawah 284,5 gram ?
Jawab.

14. Diketahui 𝜇 = 283 𝑔𝑟𝑎𝑚 ; 𝜎 = 1,6 ; 𝑥 = 284,5
𝑧 =
𝑥 − 𝜇
𝜎
=
284,5 − 283
1,6
=
1,5
1,6
= 0,94
𝑃( 𝑋 < 284,5) = 𝑃( 𝑍 < 0,94)
= 0,5 + 𝑃(0 < 𝑍 < 0,94)
= 0,5 + 0,3264
= 0,8264 atau 82,64%
Contoh. Sebuah pabrik baterai memproduksi baterai dengan daya tahan 400 jam. Jika
simpangan baku 20 jam. Berapa peluang baterai tersebut hidup antara 400 hingga 434,4
jam!
Jawab
Diketahui 𝜇 = 400; 𝜎 = 20; 𝑥1 =
400; 𝑥2 = 434,4
𝑧1 =
𝑥1 − 𝜇
𝜎
=
400 − 400
20
=
0
20
= 0
𝑧2 =
𝑥2 − 𝜇
𝜎
=
434,4 − 400
20
=
34,4
20
= 1,72
𝑃(400 < 𝑋 < 434,4) = 𝑃(0 < 𝑍 < 1,72)
𝑃(0 < 𝑍 < 1,72) = 0,4573
Contoh. Sebuah permen dipotong dengan rata-rata 25 mm. Dengan simpangan baku 2 cm.
Berapa persenkah kemungkinan permen diproduksi dengan panjang dibawah 23 mm?
Jawab.

15. Diketahui 𝜇 = 25 𝑚𝑚 ; 𝜎 = 2 ; 𝑥 = 23
𝑧 =
𝑥 − 𝜇
𝜎
=
23 − 25
2
=
−2
2
= −1
𝑃( 𝑍 < −1) = 0,5 − 𝑃(0 < 𝑧 < 1)
= 0,5 − 0,3413
= 0,1587 atau 15,87%
Contoh. Sebuah alat elektronik diberikan jaminan tak akan rusak rata-rata 800 hari. Dengan
simpangan baku 40 hari. Berapa peluang alat elektronik tersebut tak akan rusak antara 778
hari sampai 834 hari
Jawab.
Diketahui 𝜇 = 800; 𝜎 = 40; 𝑥1 =
778; 𝑥2 = 834
𝑧1 =
𝑥1−𝜇
𝜎
=
778−800
40
=
−22
40
= −0,55
𝑧2 =
𝑥2 − 𝜇
𝜎
=
834 − 800
40
=
34
40
= 0,85
𝑃(778 < 𝑋 < 834)
= 𝑃(−0,55 < 𝑍 < 0,85)
𝑃(−0,55 < 𝑍 < 0,85)
= 𝑃(0 < 𝑍 < 0,55)
+ 𝑃(0 < 𝑍 < 0,85)
𝑃(0,5 < 𝑍 < 0,85) = 0,2088 + 0,3023 = 0,5111 atau 51,11%
Contoh. PT Work Electric, memproduksi Bohlam Lampu yang dapat hidup rata-rata 900
jam dengan simpangan baku 50 jam. PT Work Electric ingin mengetahui berapa persen
produksi pada kisaran antara 800-1.000 jam, sebagai bahan promosi bohlam lampu. Hitung
berapa probabilitasnya!
Jawab:
Diketahui 𝜇 = 900; 𝜎 = 50; 𝑥1 = 800; 𝑥2 = 1000
𝑧1 =
𝑥1 − 𝜇
𝜎
=
800 − 900
50
=
−100
50
= −2,00

16. 𝑧2 =
𝑥2 − 𝜇
𝜎
=
1000 − 900
50
=
100
50
= 2,00
𝑃(800 < 𝑋 < 1000) = 𝑃(−2,00 < 𝑍 < 2,00)
𝑃(−2,00 < 𝑍 < 2,00)
= 𝑃(−2,00 < 𝑍 < 0)
+ 𝑃(0 < 𝑍 < 2,00)
𝑃(0,5 < 𝑍 < 0,85) = 2𝑃(0 < 𝑍 < 2,00) =
2(0,4772) = 0,9544 atau 95,44%
Jadi 95,44% produksi berada pada kisaran 800-1.000 jam. Jadi jika PT Work Electric
mengklaim bahwa lampu bohlamnya menyala 800-1.000 jam, mempunyai probabilitas
benar 95,44%, sedang sisanya 4,56% harus dipersiapkan untuk garansi.
PendekatanDistribusi Binomial dengan Distribusi Normal
Pendekatan distribusi normal terhadap distribusi binomial dengan menggunakan
rata-rata binomial 𝜇 = 𝑛𝑝 dan simpangan baku binomial 𝜎 = √ 𝑛𝑝𝑞, asalkan 𝜇 dan 𝜎
keduanya lebih besar dari 5.
Contoh. Misalkan suatu distribusi variabel acak diskrit X dengan 𝑛 = 300 dan 𝑝 = 0,25.
Tentukan nilai 𝑃( 𝑋 > 90)
Jawab.
Rata-rata 𝜇 = 𝑛𝑝 = 300.0,25 = 75
Simpangan baku 𝜎 = √ 𝑛𝑝𝑞 = √300.0,25(1 − 0,25) = √300.0,25.0,75 = √56,25 = 7,5
𝜇 dan 𝜎 keduanya lebih besar dari 5, sehingga syarat pendekatan normal terhadap distribusi
binomial dipenuhi.
Nilai Z ditentukan 𝑍 =
𝑥−𝜇
𝜎
=
90−75
7,5
=
15
7,5
= 2
𝑃( 𝑋 > 90) = 𝑃( 𝑍 > 2) = 0,5 − 𝑃(0 < 𝑍 < 2) = 0,5 − 0,4772 = 0,0228
Contoh. Jika dari hasil survey di suatu daerah, 15% penduduk mempunyai penyakit mag, Jika kita
mengambil sampel 100 orang, maka tentukan peluang
a. Banyaknya orang yang kena mag adalah maksimal 20 orang
b. Banyaknya orang yang kena mag lebih dari 18 orang
Jawab.

17. Diketahui banyaknya percobaan (sampel orang yang dipilih) adalah n=100
Peluang berhasil (peluang mempunyai sakit mag) adalah p=0,15
Peluang gagalnya q=1−p=0,85
Rata-rata 𝜇 = 𝑛𝑝 = 100.0,15 = 15
Simpangan baku 𝜎 = √ 𝑛𝑝𝑞 = √100.0,15(1 − 0,15) = √100.0,15.0,85 = √12,75 = 3,5
a. X = 20
Nilai 𝑍 =
𝑥−𝜇
𝜎
=
20−15
3,5
=
5
3,5
= 1,43
𝑃( 𝑋 ≤ 20) = 𝑃( 𝑍 ≤ 1,43) = 0,5 + 𝑃(0 ≤ 𝑍 ≤ 1,43) = 0,5 + 0,4236 = 0,9236
Jadi dari 100 orang peluang yang kena mag maksimal 20 orang adalah 0,9236
b. X = 18
Nilai 𝑍 =
𝑥−𝜇
𝜎
=
18−15
3,5
=
3
3,5
= 0,86
𝑃( 𝑋 > 18) = 𝑃( 𝑍 > 0,86) = 0,5 − 𝑃(0 < 𝑍 < 0,86) = 0,5 − 0,3051 = 0,1949
Jadi dari 100 orang peluang yang kena mag lebih dari 18 orang adalah 0,1949
Contoh. Sebuah pabrik lampu neon dari hasil pendataan produksinya, diperoleh
sekitar 4% produksinya cacat. Jika dipilih 3000 lampu secara acak, maka tentukan peluang
mendapatkan maksimal 100 buah lampu yang rusak
Jawab
Diketahui banyaknya percobaan(banyak lampu dipilih) adalah n=3000
Peluang berhasil (peluang mendapatkan lampu rusak) adalah p=4%=0,04
Peluang gagalnya q=1−p= 1 – 0,04 = 0,96
Rata-rata 𝜇 = 𝑛𝑝 = 3000.0,04 = 120
Simpangan baku 𝜎 = √ 𝑛𝑝𝑞 = √3000.0,04.0,96 = 115,2
Nilai 𝑍 =
𝑋−𝜇
𝜎
=
100−120
115,2
=
−20
115 ,2
= 0,17
𝑃( 𝑋 ≤ 100) = 𝑃( 𝑍 ≤ 0,17) = 0,5 + 𝑃(0 ≤ 𝑍 ≤ 0,17) = 0,5 + 0,0675 = 0,5675

18. Tabel Distribusi Normal Baku