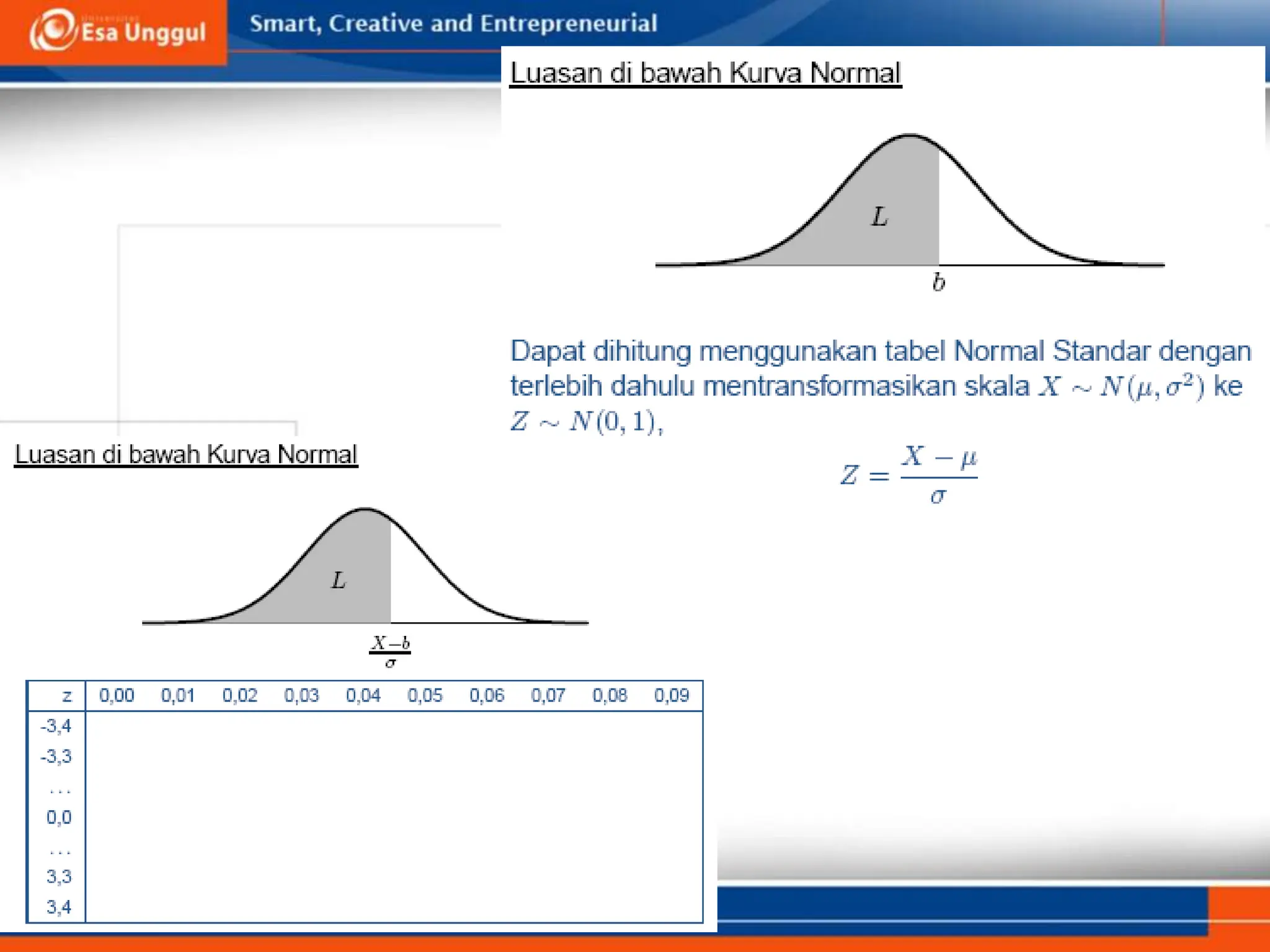
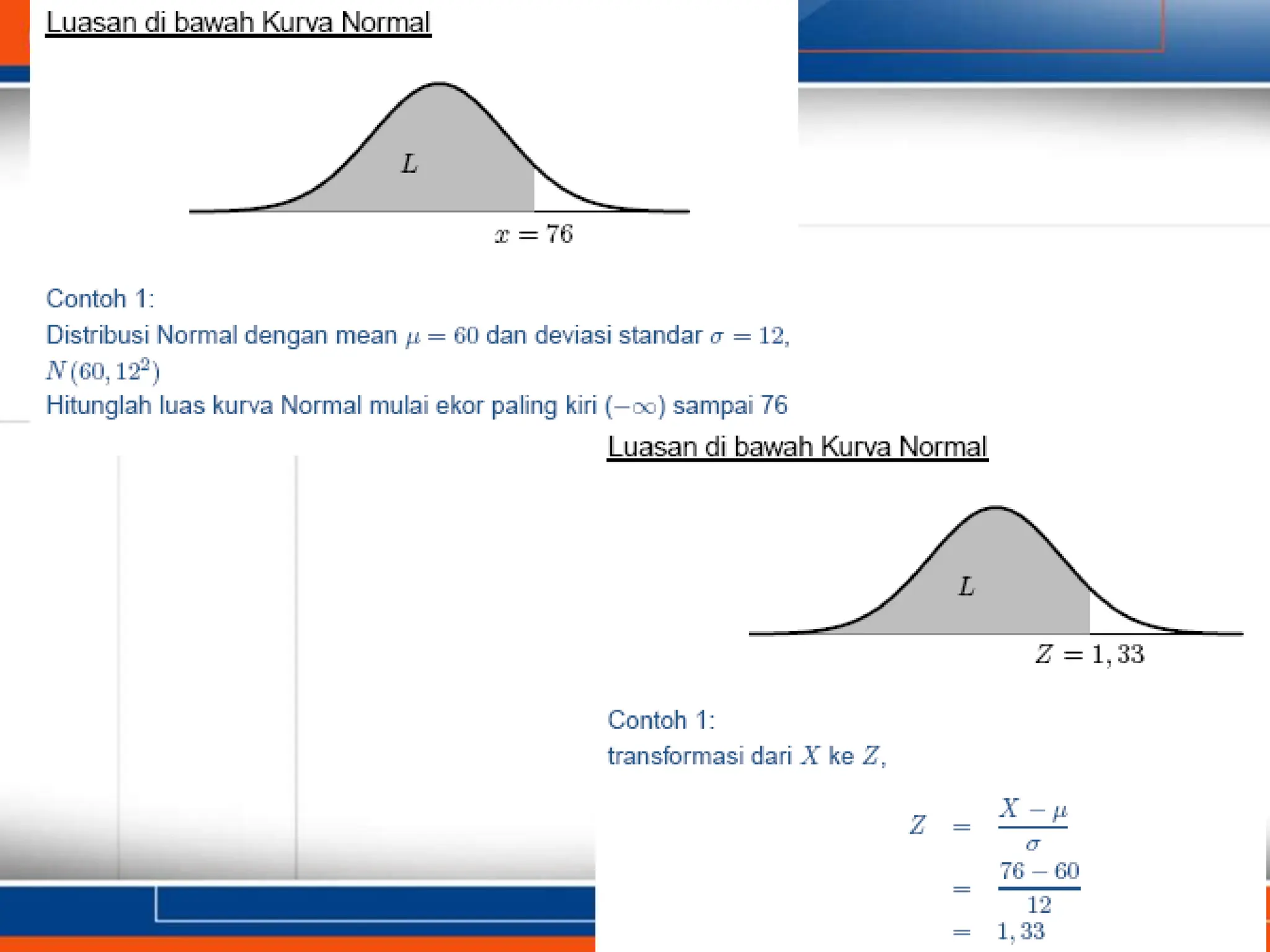
Dokumen ini membahas tentang distribusi probabilitas, mencakup variabel random diskrit dan kontinu, serta model matematik yang menghubungkan nilai variabel random dengan peluang terjadinya masing-masing nilai. Contoh-contoh yang diberikan termasuk distribusi binomial, hipergeometrik, Poisson, dan normal. Kesimpulannya, distribusi peluang sangat penting dalam statistika dan dapat diperlihatkan dalam berbagai bentuk seperti fungsi, tabel, atau grafik.

1. PERTEMUAN 11
DISTRIBUSI PROBABILITAS
PELAKASANA AKADEMIK MATA KULIAH UMUM
1

2. DISTRIBUSI PROBABILITAS
Tujuan: Memahami ditribusi probabilitas diskrit dan kontinu
Statistics UEU 2017

3. Variabel Random
• Variabel random diskrit: Suatu variabel random yang
hanya dapat menjalani harga-harga yang berbeda yang
berhingga banyaknya (sama banyaknya dengan
bilangan bulat)
• Variabel random kontinu: Suatu variabel random yang
dapat menjalani setiap harga dalam suatu interval (tak
berhingga banyaknya)
• Distribusi Peluang: Model matematik yang
menghubungkan semua nilai variabel random dengan
peluang terjadinya nilai tersebut dalam ruang sampel.
Distribusi peluang dapat direpresentasikan dalam bentuk
fungsi, tabel, atau grafik. Distribusi peluang dapat
dianggap sebagai frekuensi relatif jangka panjang.

4. Definisi dan Contoh
• Var random X adalah fungsi dari S ruang sampel ke bilangan
real R X : S  R
• Contoh : Menjawab soal multipel choice 2 kali
S = {SS, SB, BS, BB}
• X : VR Banyaknya jawaban benar, maka X = {0,1,2}
BB
SB
BS
SS
0
1
2
R
X
S
Statistics UEU 2017

5. Peluang dan Variabel Random

6. Peluang dan Variabel Random

7. Variabel Random
• Distribusi Peluang Diskret
• Contoh
• Distribusi banyaknya sisi muka yang muncul dalam pelemparan mata uang
logam tiga kali.

8. Variabel Random
• Distribusi Peluang Kontinu (Fungsi Densitas)
• Contoh Fungsi densitas suatu variabel random X

9. Variabel Random
=Ukuran dispersi

10. Variabel Random

11. Variabel Random
Dua Variabel Random
• Ada dua variabel random yang diamati bersamaan
dalam suatu eksperimen.
Contoh:
• Sebuah mata uang logam dilemparkan tiga kali.
X: banyaknya M muncul dalam dua lemparan pertama
Y : banyaknya M muncul dalam lemparan ketiga
• Distribusi peluang untuk dua variabel random disebut
sebagai distribusi peluang bersama

12. Peluang dan Variabel Random

13. Variabel Random

14. Variabel Random

15. VARIABEL RANDOM
X
DISKRIT KONTINU












b
a
x
X
x
x
X
P
b
X
a
P
x
X
P
x
X
P
)
(
)
(
.
3
1
)
(
.
2
0
)
(
.
1  
 
 dx
x
f
b
X
a
P
dx
x
f
x
f
b
a
A
x








)
(
.
3
1
.
2
0
.
1
Diagram karakteristik perbedaan probabilitas
diskrit dan kontinu
Statistics UEU 2017

16. VARIABEL RANDOM DALAM STATISTIKA
BERNOULLI
BINOMIAL
MULTINOMIAL
GEOMERIK
HIPERGEOMETRIK
POISSON
DISKRIT:
VARIABEL
RANDOM
KONTINU NORMAL
UNIFORM KONTINU
BETA
GAMMA
EXPONENTIAL
WEIBULL
CAUCHY
DOUBLE EXPONENTIAL
Statistics UEU 2017

17. Distribusi Variabel Random Diskrit
• Eksperimen Bernoulli
• Eksperimen dengan hanya dua hasil yang mungkin
• Contoh
– melempar mata uang logam satu kali
– Mengamati telur ayam, apakah anak ayam itu jantan atau
betina
– Mengamati kedelai yang ditanam, tumbuh atau tidak
– Reaksi obat pada tikus, positif atau negatif

18. Distribusi Variabel Random Diskret
• Sifat-sifat Eksperimen Bernoulli
– tiap usaha (trial) menghasilkan satu dari dua hasil
yang mungkin, dinamakan sukses (S) dan gagal
(G);
– peluang sukses, P(S) = p dan peluang gagal P(G) =
1 − p, atau P(G) = q;
– usaha-usaha tersebut independen

19. Distribusi Variabel Random Diskret

20. Distribusi Variabel Random Diskret

21. n
x
q
p
x
n
x
X
P
x
f x
n
x
,...,
1
,
0
,
)
(
)
( 










 
• Ada x kejadian sukses dengan peluang px dan n-x
kejadian sukses gagal dengan peluang (1-p)n-x
Statistics UEU 2017

22. Distribusi Variabel Random Diskret dan Kontinu

23. Distribusi Variabel Random Diskret dan Kontinu

24. Contoh (Distribusi Binomial)
• Suatu uang logam yang baik (seimbang) dilempar 4 kali. X
adalah banyaknya muka muncul dalam 4 kali pelemparan
tersebut. Tentukan probabilitas munculnya muka
• Pelemparan dipandang sebagai usaha, dan sukses adalah
muka muncul. X merupakan variabel random binomial dengan
n = 4 dan p = 1/2 dengan distribusi peluang:

25. Contoh : jika diamati 15 orang mahasiswa, berapakah probabilitas
mendapat 9 orang dengan nilai A ? Berapakah rata yang mendapat
nilai A ?
Dengan menunjukkan bahwa
X = banyaknya yang mendapat nilai A
adalah variabel random binomial dengan n = 15 dan p =
5
1
 
...
)
8
X
(
P
9
X
P
5
4
5
1
!
6
!
9
!
15
5
4
5
1
9
15
)
9
X
(
P
)
9
(
f
6
9
9
15
9










































dihitung langsung
menggunakan tabel distribusi binomial
5
1
.
15

 np

Statistics UEU 2017

26. Distribusi Variabel Random Diskrit
Eksperimen hipergeometrik:
Dalam populasi berukuran N sebanyak k dinamakan sukses sedangkan
sisanya N − k dinamakan gagal
sampel berukuran n diambil dari N benda
Cara pengambilan sampel tanpa pengembalian

27. Contoh (Distribusi Hipergeometrik)
• Suatu kotak berisi 40 suku cadang dengan 3 rusak. Sampel
berukuran 5 diambil sekaligus dari kotak. Pengambilan sampel ini
adalah suatu eksperimen hipergeometrik dengan X adalah
banyaknya suku cadang rusak, N = 40, n = 5 dan k = 3 dengan
distribusi peluang:

28. Distribusi Poisson
,...
2
,
1
,
0
x
;
!
x
e
)
;
x
(
f
x






• Var X~Pois(µ)
– X = jumlah kejadian
tertentu dalam satuan
unit waktu atau ruang
– µ = rata-rata kejadian
– E(X) = V(X) = µ
• Contoh
– Banyaknya telepon dalam
periode tertentu
– Banyaknya pelanggan pada
counter
– Banayknya kcelakaan
– Banyaknya mesin rusak
– dll
Statistics UEU 2017
Sifat-sifat eksperimen Poisson:
 banyaknya sukses terjadi dalam suatu selang waktu
atau daerah tertentu tidak terpengaruh (bebas) dari
apa yang terjadi pada interval waktu atau daerah
yang lain,

29.  peluang terjadinya sukses dalam interval waktu yang singkat atau
daerah yang sempit sebanding dengan panjang interval waktu, atau luas
daerah dan tidak tergantung pada banyaknya sukses yang terjadi di luar
interval waktu atau daerah tersebut,
 peluang terjadinya lebih dari satu sukses dalam interval waktu yang
singkat atau daerah yang sempit tersebut dapat diabaikan.
 X ~ Binomial(n, p)
 Bila n besar dan n kecil,
– Binomial(n, p) → Poisson(λ), dengan λ = np
 X adalah banyaknya sukses dalam eksperimen Poisson, yang
mempunyai distribusi probabilitas
 Mean dan Variasi

31. Contoh (Distribusi Poisson)
• Rata-rata banyaknya partikel radioaktif yang melewati suatu
counter selama 1 milidetik dalam suatu percobaan di
laboratorium adalah 4. Peluang 6 partikel melewati counter
dalam suatu milidetik tertentu adalah

33. • Distribusi Normal dengan mean E(X) = μ dan variansi
• Var(X) = σ2 (ditulis N(μ, σ2 ) mempunyai fungsi peluang,
fumgsi probabilitas:
•  = 3, 141593 . . . Dan e = 2, 718282 . . .
• Distribusi Normal standar: distribusi Normal dengan
mean 0 dan variansi 1, ditulis N(0, 1)
Distribusi Normal
• Transformasi
diperoleh distribusi normal yang khusus sehingga tabelnya efisien
0
;
,
;
2
1
)
,
,
(
)
;
(
~
2
2
1
2
2
2
2













 










x
e
x
f
N
X
x
1
)
Z
(
V
;
0
)
Z
(
E
;
e
2
1
)
z
(
f
X
Z
2
z
z
2
z2















34. zo 0 1 2 … 7 8 9
0,0 0,5000 0,5004 0,5080 0,5279 0,5319 0,5359
0,1 0,5398 0,5348 0,5478 0,5675 0,5714 0,5754
0,2 0,5793 0,5832 0,5871 0,6064 0,6103 0,6141
.
.
.
1,0 0,8413 0,8438 0,8461 0,8577 0,8599 0,8621
1,1 0,8643 0,8665 0,8686 0,8790 0,8810 0,8830
1,2 0,8849 0,8869 0,8888 0,8980 0,8997 0,9015
.
.
.
2,5 0,9938 0,9940 0,9941 0,9949 0,9951 0,9952
2,6 0,9953 0,9955 0,9956 0,9962 0,9963 0,9964
2,7 0,9965 0,9966 0,9967 0,9972 0,9973 0,9974
Tabel normal standart
zo
0 Z
Statistics UEU 2017

36. Distribusi Variabel Random Kontinu

37. Distribusi Variabel Random Kontinu

38. Distribusi Variabel Random Kontinu

41. Distribusi Variabel Random Kontinu

42. Luasan di bawah Kurva Normal
Contoh 2:
Distribusi Normal dengan mean μ = 60 dan deviasi standar σ = 12, N(60, 122).
Hitunglah luas kurva Normal antara 60 sampai 76

43. • Luasan di bawah Kurva Normal

44. • Luasan di bawah Kurva Normal

45. Luasan di bawah
Kurva Normal:
Simetris terhadap rata-rata
µ
Rata-rata = median =
modus
σ sebagai titik belok kurva:
34 % data dalam jarak 1 σ
68 % data dalam jarak 2 σ
97 % data dalam jarak 3 σ

46. Pendekatan Normal untuk Binomial
• Teorema
• Bila X adalah variabel random binomial dengan mean μ = np
dan variansi σ2 = npq, maka untuk n besar
• merupakan variabel random normal standar.

47. Pendekatan Normal untuk Binomial
• Binomial(n = 10, p = 0, 5) → Normal

48. Pendekatan Normal untuk Binomial
Binomial(n = 100, p = 0, 5) → Normal

49. Distribusi Exponential
• P(waktu kedatangan < X ) = 1-e-λX ; X>0
– X : Sebarang nilai dari variabel random X
– Λ : rata-rata jumlah kedatangan perunit waktu
– 1/λ : rata-rata waktu antar kedatangan
Contoh : Sopir datang di jembatan tol, Nasabah datang pada
mesin ATM
Statistics UEU 2017
 
1
x
f x e 



f(
X)
X
 =
0.5  =
2.0
Contoh : Kedatangan customer 30
per jam. Berapa peluang waktu
kedatangan antar customer
lebih dari 5 menit ?
Λ = 30
)
5
(
1
)
kedatangan
( 60
5




X
P
antar
P

50. Soal:
1. Suatu uang logam yang baik (seimbang) dilempar 4 kali. X
adalah banyaknya muka muncul dalam 4 kali pelemparan
tersebut. Tentukan Probabilitas (distribusi Binomial)
munculnya muka tidak 2 kali.
2. Rata-rata banyaknya kecelakaan disuatu persimpangan jalan
raya adalah 2 per minggu. Anggap mengikuti poisson,
tentukan:
a. Peluang tidak ada kecelakaan selama 1 minggu
b. Peluang paling banyak 3 kecelakaan dlm 2 minggu
3. Nilai-nilai ujian seleksi penerimaan mahasiswa baru secara
nasional dianggap berdistribusi Normal dengan mean 45
dan deviasi standar 13. Jika hanya 32,5% calon mahasiswa
yang akan diterima, berapakah nilai terendah calon
mahasiswa yang diterima?
Statistics UEU 2017

51. 4. Diketahui N(0, 1), hitunglah P(Z ≥ 1, 5).
Statistics UEU 2017

52. Kesimpulan:
1. Distribusi Peluang merupakan Model matematik yang
menghubungkan semua nilai variabel random dengan
peluang terjadinya nilai tersebut dalam ruang sampel.
2. Distribusi peluang dapat direpresentasikan dalam
bentuk fungsi, tabel, atau grafik.
3. Distribusi peluang dapat dianggap sebagai frekuensi
relatif jangka panjang.
4. Distribusi peluang dari variabel acak bisa distribusi
diskrit maupun kontinu.
Statistics UEU 2017

53. Referensi:
1. Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers and
Keying Ye, Probabilitiy and Statistics for Engineers and
Scientists, Pearson Prentice Hall, 8th edition, 2007
2. Subhash Sharma, Applied Multivariate Techniques, , John wiley
and son
3. R Johson and D Wichern, Applied multivariate statistics,
Prentice Hall.
4. J. Supranto, M.A. ,2001, Statistika Teori dan Aplikasi, Erlangga,
Jakarta.
5. Douglas C. Montgomery, George C. Runger, 2003, Applied
Statistic and Probability for Engineer, third edition, John Wiley
and Son Inc.
Statistik UEU 2017

54. TERIMA KASIH
Statistics UEU 2017

55. Statistics UEU 2017

56. Statistics UEU 2017

57. Statistics UEU 2017

58. Statistics UEU 2017

59. Statistics UEU 2017

60. Statistics UEU 2017

61. Statistics UEU 2017

62. Statistics UEU 2017