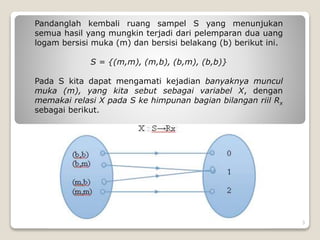
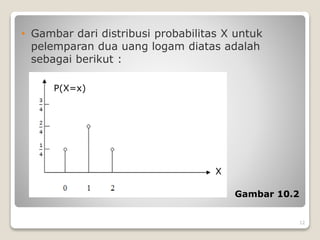
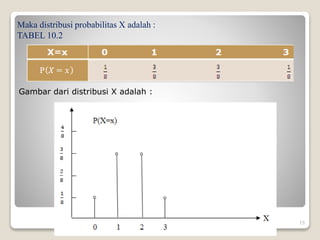
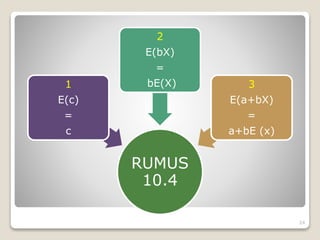
Dokumen tersebut membahas tentang distribusi probabilitas dan statistika. Secara singkat, dokumen tersebut menjelaskan: 1) Konsep distribusi probabilitas dari suatu variabel acak berdasarkan ruang sampel dan nilai-nilai variabel acaknya. 2) Cara menentukan fungsi distribusi probabilitas dan kumulatif dari suatu variabel acak. 3) Pengertian dan rumus harapan matematis sebagai ukuran rata-rata dari suatu variabel

1. DISTRIBUSI TEORITIS
Probabilitas dan Statistika
Fakultas Teknik Prodi Teknik Elektro
Untag 45 Cirebon
1

2. Pada pendahuluan statistik seringkali
yang lebih menarik perhatian untuk
diamati adalah nilai-nilai yang ditentukan
oleh titik sampel, bukan titik sampel itu
sendiri.
Pendahuluan
2

3. Pandanglah kembali ruang sampel S yang menunjukan
semua hasil yang mungkin terjadi dari pelemparan dua uang
logam bersisi muka (m) dan bersisi belakang (b) berikut ini.
S = {(m,m), (m,b), (b,m), (b,b)}
Pada S kita dapat mengamati kejadian banyaknya muncul
muka (m), yang kita sebut sebagai variabel X, dengan
memakai relasi X pada S ke himpunan bagian bilangan riil Rx
sebagai berikut.
3

4. titik (b,b) dipetakan ke nilai 0, ditulis X (b,b) = 0, sebab titik
tersebut tidak mengandung muka (m);
titik (b,m) dipetakan ke nilai 1, ditulis X (b,m) = 1, sebab titik
tersebut mengandung 1 muka (m);
titik (m,b) dipetakan ke nilai 1, ditulis X (m,b) = 1, sebab titik
tersebut mengandung 1 muka (m);
titik (m,m) dipetakan ke nilai 2, ditulis X (m,m) = 2, sebab titik
tersebut mengandung 2 muka (m).
Pada relasi X tersebut, himpunan S disebut daerah asal
(domain) sedangkan Rx = {,0,1,2} yang ,merupakan
himpunan bagian bilangan rill R disebut daerah nilai atau
daerah peta dari X tersebut;
4

5.  Perhatikan bahwa garis relasi X itu, setiap anggota S
berpasangan dengan tepat satu anggota Rx. Relasi X seperti ini
disebut pemetaan atau fungsi X. Oleh karena S oleh fungsi X
dipetakan ke himpunan bagian bilangan riil Rx {0,1,2},
maka dikatakan fungsi X bernilai Rill.
 Oleh karena titik sampel-titik sampel S, yaitu (b,b), (b,m),
(m,b), dan (m.m) terjadi secara acak atau random, maka fungsi
X disebut fungsi acak atau fungsi random. Dengan demikian,
fungsi X yang didefinisikan pada S merupakan fungsi acak
yang bernilai riil
5

6.  Suatu fungsi acak X yang bernilai riil
dimana nilai-nilainya ditentukan oleh titik
sampel-titik sampel S
 dengan S merupakan ruang sampel dari
suatu hasil percobaan statistik
variabel acak
6

7. Variabel
acak X
variabel
acak diskrit
variabel
acak kontinu
7

8. Variabel acak diskrit
adalah variabel acak yang mempunyai nilai-
nilai terhingga atau tak terhingga tetap
terbilang. Jadi, variabel acak X dapat bernilai
x1, x2, x3..., xn atau x1, x2, x3 .... xn ...; xi € R.
Variabel acak kontinu adalah variabel acak
yang nilai-nilainya tak terhingga dan tak
terbilang. Jadi, nilai-nilai variabel acak kontinu
X dapat merupakan semua nilai dalam satu
interval yang terhingga, yaitu (-, ), dimana
banyaknya bilangan yang terkandung pada
interval tersebut adalah tak terhingga dan tak
terbilang.
8

9. B. Distribusi Probabilitas
 Pada ruang sampel S tersebut bila X menyatakan
banyaknya muncul muka pada S, sebagaimana
relasi tersebut, maka nilai dari X adalah X=0,
X=1, dan X=2
Nilai X=1 berkaitan dengan titik sampel (b,b), dengan probabilitas :
P(X = 1) = P{(b,b)}= ¼
Nilai X =1, berkaitan dengan titik sampel (b,m) atau (m,b) fdengan
probabilitas:
P (X = 1)= P{(b,m)}＋ P{(m,b)} = ¼＋¼ =½
Nilai X=2, berkaitan dengan tiotik sampel (m,m) dengan probabilitas:
P (X = 2)= P{(m,m)}= ¼
9

10. Pasangan nilai-nilai variabel acak X dengan
probabilitas dari nilai-nilai X, yaitu P(X = x)
Dapat dinyatakan dalam Tabel 10.2 seperti
berikut.
X = x 0 1 2
P(X =x) ¼ ½ ¼
Bisa juga pasanagn nilai-nilai dari variabel acak X dengan
probabilitas dari nilai-nilai X, yaitu P(X = x) dituliskan
dengan pasangan terurut,yaitu:
{x1,P(X = x1)},{(x2,P( X = x2)}, {x3,P(X = x3)},...
10

11. Kumpulan pasangan nilai-nilai dari variabel acak X
dengan probabilitas nilai-nilai variabel acak X,
yaitu P(X =x) .
Distribusi X dapat dituliskan dalam bentuk tabel
atau dalam bentuk pasangan terurut.
distribusi probabilitas X
(distribusi X )
11

12. • Gambar dari distribusi probabilitas X untuk
pelemparan dua uang logam diatas adalah
sebagai berikut :
Gambar 10.2
X
P(X=x)
12

13. Contoh 10.1
 Pada pelemparan tiga uang logam, bila X
menyatakan banyaknya muncul muka (m),
tentukanlah :
a)nilai-nilai variabel acak X;
b)distribusi probabilitas X;
c)gambarlah distribusi probabilitas X!
13

14. Jawab :
Telah kita ketahui pada pembahasan Bab 9, bahwa
pelemparan tiga uang logam mempunyai ruang sampel:
S = {(m,m,m), (m,m,b), (m,b,m), (b,m,m), (b,b,m), (b,m,b), (m,b,b), (b,b,b)}
karena X menyatakan banyaknya muncul muka pada S maka
nilai-nilai dari X adalah X=0, X=1, X=2, dan X=3.
Probabilitas dari nilai-nilai X adalah :
= P 𝑋 = 0 = P{ 𝑏, 𝑏, 𝑏 } =
1
8
= P 𝑋 = 1 = P 𝑏, 𝑏, 𝑚 + P 𝑏, 𝑚, 𝑚 + P 𝑚, 𝑏, 𝑏 =
1
8
+
1
8
+
1
8
=
3
8
= P 𝑋 = 2 = P 𝑚, 𝑚, 𝑏 + P 𝑚, 𝑏, 𝑚 + P 𝑏, 𝑚, 𝑚 =
1
8
+
1
8
+
1
8
=
3
8
= P 𝑋 = 3 = P 𝑚, 𝑚, 𝑚 =
1
8
14

15. Maka distribusi probabilitas X adalah :
TABEL 10.2
Gambar dari distribusi X adalah :
15

16. X=x 2 3 4 5 6 7 8 9 10 11 12
P 𝑋 = 𝑥 1
36
2
36
3
36
4
36
5
36
6
36
5
36
4
36
3
36
2
36
1
36
Contoh 10.2
Pada pelemparan dua dadu, misalkan X adalah kejadian yang
menyatakan jumlah muka dua dadu, maka distribusi probabilitas
dari X adalah :
16

17. C. Distribusi fungsi X dan distribusi
kumulatif X
Untuk variabel acak
X diskrit :
1. f(x) = P(X=x)
2. f(x)≥0
3. 𝑥 𝑓 𝑥 = 1
Untuk variabel acak X
kontinu :
1. P(α<X<b) = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥
2. f(x) ≥0
3. −∞
∞
f x dx = 1
Jika X adalah variabel acak dan P(X=x) adalah distribusi
probabilitas dari X ,maka fungsi F(X) = P(X =x) disebut fungsi
probabilitas X atau fungsi frekuensi X atau fungsi padat
peluang X.
Sifat fungsi f(x) adalah sebagai berikut:
17

18. Rumus 10.1
F(x) =P(X≤x) =
Jika varibel acak x mempunyai fungsi probabilitas
f(x) maka fungsi distribusi kumulatif dari x, yaitu
F(x) di rumuskan sebagai berikut :
𝑋 ≤𝑥
𝑓 x 𝑏𝑖𝑙𝑎 𝑋 𝑑𝑖𝑠𝑘𝑟𝑖𝑡
−∞
𝑋
𝑓 𝑥 𝑑𝑥, 𝑏𝑖𝑙𝑎 𝑋 𝑘𝑜𝑛𝑡𝑖𝑛𝑢
18

19. Sifat distribusi kumulatif
• 0≤F(x)≤1
1
• Jika ≤ ,maka F(x1) < F(x2) ,dikatakan
fungsi F(x) monoton tidak turun
2
• F(x) diskontinu dari kiri tetapi kontinu
dari kanan
3
4
19

20. Dengan memakai fungsi distribusi kumulatif F(x)
kita dapat menentukan probabilitas dari variabel
acak X pada interval a≤X≤b, yaitu:
RUMUS
10.2
• P(a≤X≤b) = F(b) –F(a)
20

21. Contoh 10.3
Pada pelemparan 3 uang logam pada contoh 10.1 tentukanlah
a. Nilai – nilai dari fungsi distribusi probabilitas f(x)
b. Nilai –nilai dari fungsi distribusi kumulatif F(x)
Jawab:
a. Perhatikan jawaban contoh 10.1
f(x) = P(X=x), maka nilai – nilai f(x) adalah:
f(0) = P(X=0) =
1
8
f(1) = P(X=1) =
3
8
f(2) = P(X=2) =
3
8
f(3) = P(X=3) =
1
8
21

22. b. Nilai- nilai dari fungsi distribusi kumulatif F(x)
adalah sebagai berikut
F(0) = P(X≤0) = P(X=0) = f(0)=
1
8
F(1) = P(X≤1) = P(X=0)+P(X=1) =
1
8
+
3
8
=
4
8
F(2) = P(X≤2) = P(X=0)+P(X=1)+P(X=2) =
1
8
+
3
8
+
3
8
=
7
8
F(3) = P(X≤3) = P(X=0)+P(X=1)+P(X=2)+p(X=3) =
1
8
+
3
8
+
3
8
+
1
8
=
8
8
= 1
22

23. D. NILAI HARAPAN MATEMATIS
Bila variabel acak X mempunyai fungsi probabilitas f(x) = P(X=x) maka
harapan atau ekspektasi matematis atau harapan teoritis dari X yang di tulis E
(X) adalah suatu fungsi yang dirumuskan sebagai berikut
Rumus 10.3
F(x) =P(X≤x) =
Ʃx𝑓 𝑥 = ƩxP 𝑋 = 𝑥 , 𝑗𝑖𝑘𝑎 𝑥 𝑑𝑖𝑠𝑘𝑟𝑖𝑡
−00
+00
X𝑓 𝑥 𝑑𝑥, 𝑗𝑖𝑘𝑎 𝑋 𝑘𝑜𝑛𝑡𝑖𝑛𝑢
23

24. RUMUS
10.4
1
E(c)
=
c
2
E(bX)
=
bE(X) 3
E(a+bX)
=
a+bE (x)
24

25. Contoh 10.4
Pada pelemparan 3 uang logam ,tentukan harapan matematis
banyaknya muncul muka pada tiap pelemparan!
 Jawab:
Perhatikan fungsi distribusi probabilitas X pada jawaban Contoh 10.1
dimana X menunjukan banyaknya muncul muka.Karena X diskrit ,maka
harapan matematis banyaknya muncul muka adalah:
25

26. Contoh 10.5
Pada pelemparan 2 dadu,tentukanlah harapan matematis
jumlah muka 2 dadu
Jawab:
Perhatikan fungsi distribusi probabilitas X pada jawaban contoh
10.2 dimana X menyatakan jumlah muka 2 dadu. Karena X diskrit
maka harapan matematis munculnya jumlah muka 2 dadu adalah
26

27. D. KEGUNAAN NILAI HARAPAN
MATEMATIS
 Salah satu manfaat yang sangat penting dari harapan
matematis adalah dapat dipakai untuk menentukan
mean (µ) dan variasi (𝜎2
). Atau standar deviasi (Ơ)
dari parameter yang dirumuskan sebagai berikut :
1. Mean populasi µ 𝐸(𝑥)
2. Variasi polulasi :
𝜎2
= 𝐸 𝑥 − 𝜇 2
=
E 𝑥 − 𝜇 2
𝑓 𝑥 , 𝑗𝑖𝑘𝑎 𝑥 𝑑𝑖𝑠𝑘𝑟𝑖𝑡
−∞
∞
𝑥 − 𝜇 2𝑓 𝑥 𝑑𝑥 , 𝑗𝑖𝑘𝑎 𝑥 𝑘𝑜𝑛𝑡𝑖𝑛𝑢
3. Standar Deviasi 𝜎 = 𝐸{ 𝑥 − 𝜇 2
27

28. Perhatikan bahwa rumus variasi dapat
disederhanakan menjadi rumus berikut ini, dengan
memakai sifat-sifat harapan matematis pada
rumus 10.4
Rumus 10.6
• Dengan demikian rumus variasi 𝜎2 menjadi
28

29. Contoh 10.6
Tentukanlah mean standart deviasi dari banyaknya muka pada
pelemparan tiga uang logam!
Jawab :
Perhatikan jawaban pada contoh 10.1 dan contoh 10.4.
Mean adalah 𝜇 = 𝐸 𝑋 = 1,5
Variasi 𝜎2 = 𝐸 𝑋2 − 𝜇2
𝐸 𝑋2 =
𝑥=0
3
𝑥2 P
= 0 2
P 𝑋 = 0 + 1 2
P 𝑋 = 1 + 2 2
P 𝑋 = 2 + + 3 2
P 𝑋 = 3
= 0
1
8
+ 1
3
8
+ 4
3
8
+ 9
1
8
=
24
8
= 3
Maka 𝜎2
= 3 − 1,5 2
= 3 − 2,25 = 0,75
Jadi, standar deviasi 𝜎 = 0,75 = 0,87
29

30. Contoh 10.7
Bila X menyatakan munculnya jumlahmuka pada pelemparan dua
dadu, tentukanlah mean dan standar deviasi X !
Jawab :
Perhatikan jawaban pada contoh 10.2 dan contoh 10.5
Mean X adalah 𝜇 = 𝐸 𝑋 = 7
Variansi x adalah 𝜎2 = 𝐸 𝑋2 − 𝜇2
𝐸 𝑋2
=
𝑥=12
12
𝑥2
P 𝑋 = 𝑥
= 2 2
1
36
+ 3 2
2
36
+ 4 2
3
36
+ 5 2
4
36
+ 6 2
5
36
+ 7 2
6
36
+ 8 2
5
36
+ 9 2
4
36
+ 10 2
3
36
+ 11 2
2
36
+ 12 2
1
36
=
4
36
+
18
36
+
48
36
+
100
36
+
180
36
+
294
36
+
320
36
+
324
36
+
300
36
+
242
36
+
144
36
=
1974
36
Variansi 𝜎2 =
1974
36
− 7 2 =
1974−1764
36
=
210
36
Jadi, standar x adalah 𝜎 =
210
36
= 2,42
30

31. Contoh soal dan pembahasan nomor 4
 Dalam suatu bisnis tertentu, seorang dapat memperoleh
keutungan sebesar R 3.000.000,00 dengan probilitas 0,6
atau menderita kerugian sebesar Rp 1000.000,00 dengan
probabilitas 0,4. Tentukanlah nilai harapannya !
 Jawab :
 Misalkan X = keuntungan yang diperoleh dalam bisnis
 P(X=x) = Probabilitas memperoleh keuntungan tersebut.
 Maka nilai X1 = 3.000.000 dengan probabilitas P (X=
3.000.000) = 0,6 dan X2 = -1.000.000 dengan probabilitas P
(X= -1.000.000) = 0,4.
 Nilai harapan X adalah :
 E(X) = 3.000.000 (0,6) – 1.000.000 (0,4) = 1.400.000.
 Karena nilai harapan positif, maka bisnis itu memberi
harapan keuntungan sebesar Rp 1.400.000,00. Makin besar
nilai harapan, maka besar juga keuntungannya.
31

32. Contoh soal pembahasan nomor 5
 Suatu pengiriman 6 pesawat televisi berisi 2
yang rusak.
 Sebuah hotel membeli 3 pesawat televisi
secara acak dari kiriman tersebut. Bila X
menyatakan banyaknya televise yang rusak
yang dibeli hotel tersebut, tentukanlah:
a. Distribusi probabilitas X
b. Nilai harapan X
c. Simpangan baku X
32

33. Televisi baik = 4, Televisi rusak = 2, dan
televise yang di beli = 3
Kombinasi televisi yang dibeli adalah terdiri
atas :
3 baik dan 0 rusak dengan kombinasi 4
3
2
0
2 baik dan 1 rusak dengan kombinasi 4
2
2
1
1 baik dan 2 rusak dengan kombinasi 4
1
2
2
Seluruh kombinasi adalah 6
3
33

34. Bila X menyatakan banyaknya televisi rusak,
maka nilai-nilai X adalah 0,1, dan 2, masing-
masing dengan probabilitas :
P(X = 0) =
4
3
2
0
6
3
=
4 1
(20)
=
1
5
P(X = 1) =
4
2
2
1
6
3
=
6 2
(20)
=
3
5
P(X = 2) =
4
1
2
2
6
3
=
4 1
(20)
=
1
5
34

35. Catatan X = 0 artinya dari 3 televisi yang dibeli hotel
terdapat 0 televisi rusak ( tidak ada rusak )
= 1 artinya dari 3 televisi yang dibeli hotel
terdapat 1 televisi rusak
= 2 artinya dari 3 televisi yang dibeli hotel
terdapat 2 televisi yang rusak
35

36. b. Nilai harapan E(X) = (0)
1
5
+ (1)
3
5
+ (2)
1
5
= 1
c. E(X2) = (0)2 1
5
+ (1)2 3
5
+ (2)2 1
5
=
7
5
σ2 = E(X2) – E(X) =
7
5
– 1 =
2
5
= 0,4
simpangan baku σ = 0,4 = 0,63
Nilai maksimum X = 2, sebab hanya ada 2 televisi
rusak.
a. jadi distribusi probabilitas X adalah sebagai
berikut :
Tabel 10.5
X 0 1 2
P (x)
1
5
3
5
1
5
36