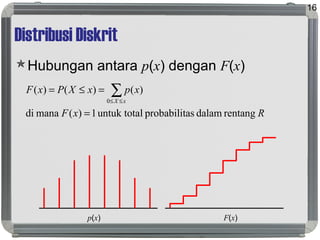
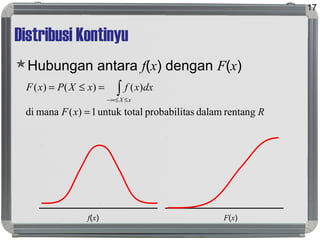
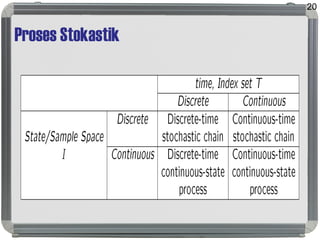
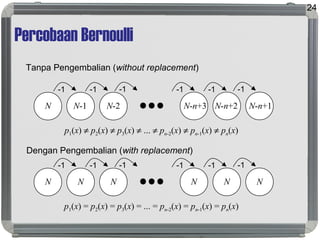
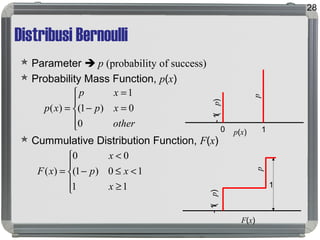
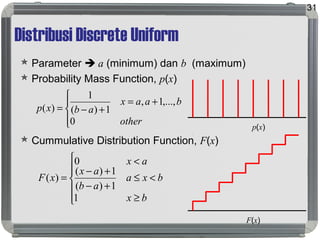
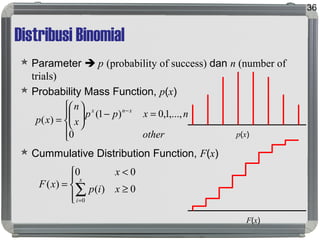
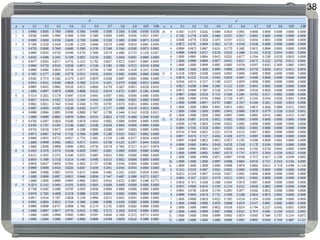
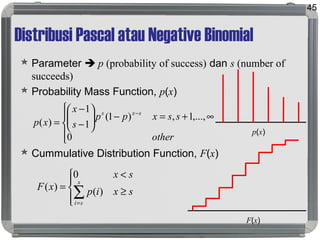
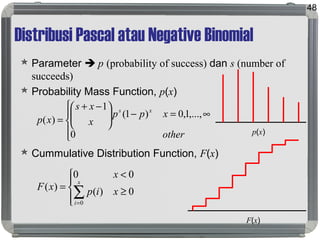
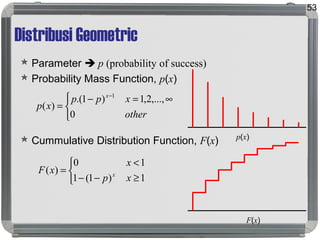
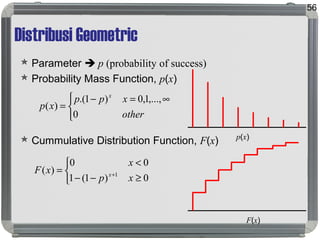
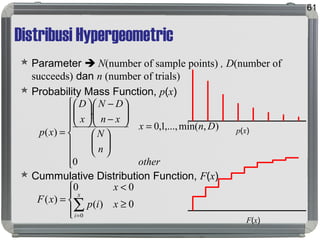
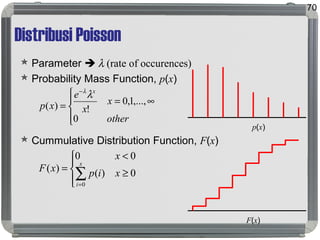
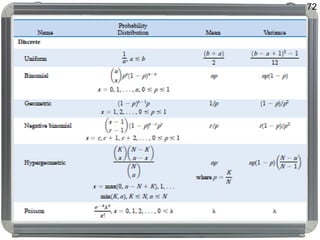
Dokumen tersebut membahas tentang distribusi probabilitas yang mencakup ruang sampel dan variabel acak, distribusi empiris dan teoritis, fungsi probabilitas seperti probability mass function, probability density function, dan cumulative distribution function, serta proses stokastik seperti proses Bernoulli dan proses Poisson."