Downloaded 142 times
Uploaded byArif Rahman
Stat prob10 distribution_normal
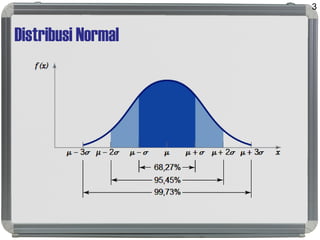
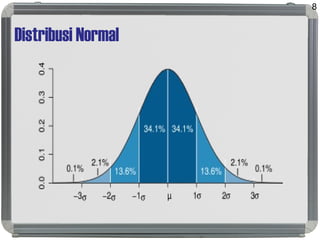
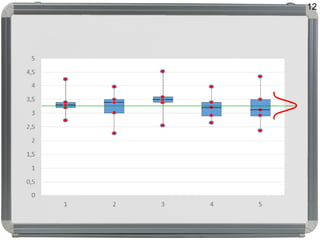
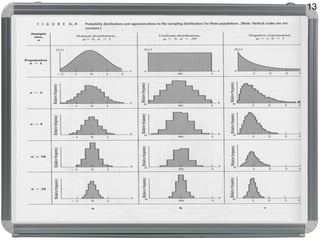
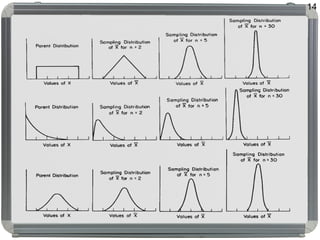
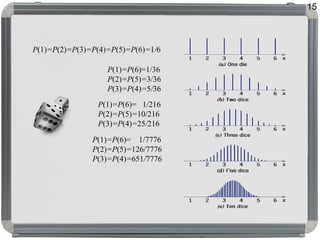
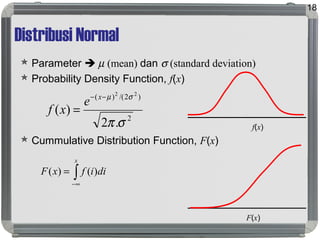
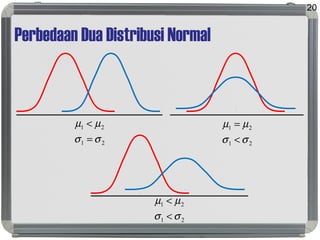
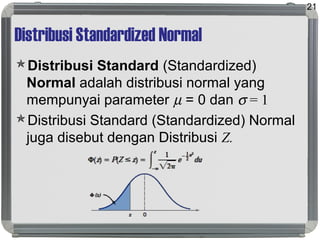
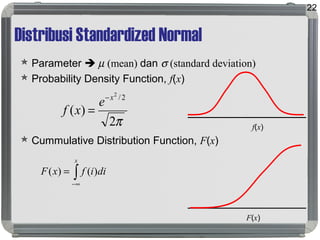
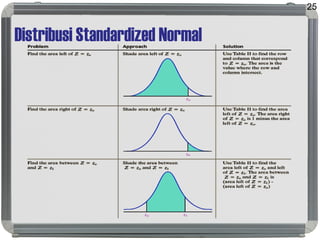
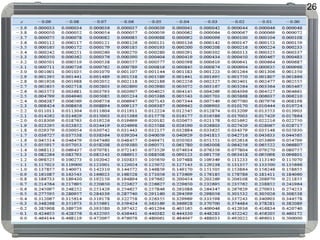
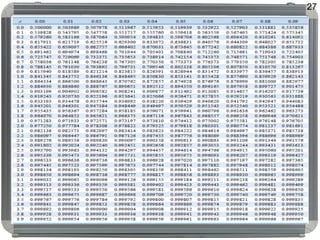
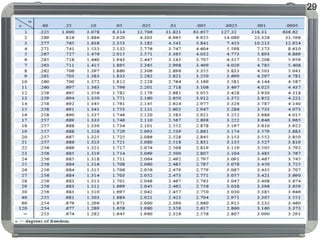
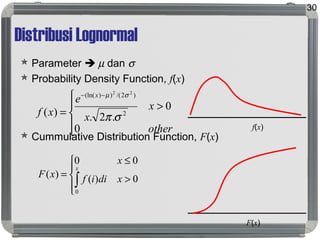
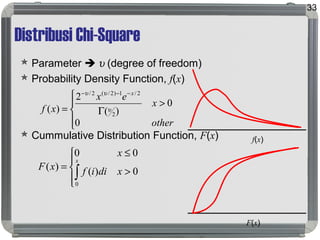
Dokumen ini membahas distribusi normal, karakteristik, sejarah, dan penerapannya dalam statistik serta hubungannya dengan distribusi lain seperti t, lognormal, chi-square, dan f. Distribusi normal ditandai dengan kurva simetris berbentuk lonceng, parameter mean (μ) dan standard deviation (σ), serta konsep dasar seperti central limit theorem dan law of large numbers. Selain itu, dijelaskan juga mengenai distribusi standard normal dan bagaimana beberapa distribusi terkait ditemui dalam pengukuran ilmiah.
More Related Content
Similar to Stat prob10 distribution_normal
Stat prob10 distribution_normal
- 1. DISTRIBUSI PROBABILITAS : DistribusiNormal ARIF RAHMAN 1
- 2. Sekilas Distribusi Normalatau Gaussian Distribusi Normal atau Gaussian termasuk distribusi variabel kontinyu. Kurva distribusi berbentuk lonceng (bell- shaped distribution) Distribusi Normal dirumuskan bermula dari observasi pada model sebaran error atau residual dalam pengukuran ilmiah yang mengikuti pola simetris dalam distribusi berbentuk lonceng. 2
- 3.
- 4. Tokoh Statistik TerkaitDistribusi Normal Abraham DeMoivre (1733) Laplace (1775) Legendre (1805) Karl Friedrich Gauss (1809) 4 Gauss 1777-1855 De Moivre 1667-1754 Laplace 1749-1827 Legendre 1752-1833
- 5. Sifat Penting DistribusiNormal 1. Rentang variabel acak meliputi semua bilangan nyata dari negatif tak hingga sampai positif tak hingga (-∞ < x < ∞) 2. Nilai fungsi probabilitas (pdf) bernilai positif untuk semua variabel acak (f(x) > 0) 3. Total probabilitas bernilai sebesar 1 4. ... 5 =∫ ∞ ∞− 1)( dxxf
- 6. Sifat Penting DistribusiNormal 3. ... 4. Nilai mean, median dan mode berimpit. 5. Kurva simetris dengan pembatas pada nilai rata-rata atau mean sebagai axis vertikal. 6. Titik belok atau perubahan fungsi kurva (inflection points) di µ+σ, pada bagian tengah cembung (concave downward) dan pada sisi luar (tail) cekung (concave upward) 7. ... 6
- 7. Sifat Penting DistribusiNormal 6. ... 7. Nilai fungsi probabilitas simetris terhadap mean. 8. Nilai fungsi probabilitas di kedua ujung (tail) distribusi mengecil. 7 ( )0)(limdan0)(lim == ∞→−∞→ xfxf xx )()( xfxf ∆+=∆− µµ
- 8.
- 9. Dua Bilangan KonstantaSpesial Bilangan natural (e) Bilangan phi (π) 9 028759045235367182818284,2 !3!2 11lim 32 = +−+−= −=− ∞→ e aa a n a e n a n 264389793238461415926535,3 7 1 5 1 3 1 14lim = +−+−= ∞→ π π n
- 10. The Law ofLarge Number Semakin banyak data ditambahkan dalam observasi atau eksperimen, maka selisih antara statistik rata-rata sampel (x) dengan parameter rata-rata populasi (µ) adalah sangat kecil atau mendekati 0 (nol). Data observasi atau eksperimen yang sangat banyak mempunyai statistik sampel (x dan s) sebagai pendekatan parameter populasi (µ dan σ) 10
- 11. Central Limit Theorem Jikasebuah variabel x adalah rata-rata sederet variabel acak independent dengan ukuran sampel yang sangat besar, maka distribusi rata-rata sampel tersebut mendekati distribusi normal dengan pendekatan rata-rata dan simpangan baku 11 n s N x nN x x x x = === ∑∑ σ µ )/(
- 12.
- 13.
- 14.
- 15.
- 16. Distribusi Normal Distribusi Normalmenunjukkan sebaran variabel acak yang membentuk pola simetris berbentuk lonceng dengan laju λ. Variabel acak meliputi semua bilangan nyata mulai dari negatif tak hingga (-∞) sampai tak hingga (∞), X∈{-∞<x<∞}. 16
- 17. Distribusi Normal Penerapan DistribusiNormal antara lain untuk menunjukkan sebaran data hasil pengukuran ilmiah baik observasi ataupun eksperimen, sebaran kesalahan, sebaran rata-rata data subgrup, sebaran data yang sangat banyak (Law of Large Number dan Central Limit Theorem). 17
- 18. Distribusi Normal Parameter µ (mean) dan σ (standard deviation) Probability Density Function, f(x) Cummulative Distribution Function, F(x) 18 2 )2/()( .2 )( 22 σπ σµ−− = x e xf f(x) F(x) ∫∞− = x diifxF )()(
- 19. Distribusi Normal Dinotasikan denganN(x;µ,σ) Parameter µ dan σ Mean Variance 19 µµ = 22 σσ =
- 20. Perbedaan Dua DistribusiNormal 20 21 21 σσ µµ = < 21 21 σσ µµ < = 21 21 σσ µµ < <
- 21. Distribusi Standardized Normal DistribusiStandard (Standardized) Normal adalah distribusi normal yang mempunyai parameter µ = 0 dan σ = 1 Distribusi Standard (Standardized) Normal juga disebut dengan Distribusi Z. 21
- 22. Distribusi Standardized Normal Parameter µ (mean) dan σ (standard deviation) Probability Density Function, f(x) Cummulative Distribution Function, F(x) 22 π2 )( 2/2 x e xf − = f(x) F(x) ∫∞− = x diifxF )()(
- 23. Distribusi Standardized Normal Dinotasikandengan Z(x) Parameter µ dan σ Mean Variance 23 0=µ 12 =σ
- 24. Distribusi Standardized Normal HubunganDistribusi Standard (Standardized) Normal dengan Distribusi Normal Jika X adalah variabel acak independen berdistribusi Normal (µ,σ), maka adalah variabel acak berdistribusi Standard Normal 24 σ µ− = X Z
- 25.
- 26.
- 27.
- 28. Distribusi Student’s t DistribusiStudent’s t adalah sebaran variabel acak yang merupakan model gabungan variabel acak X berdistribusi Standard Normal yang mempunyai parameter µ=0 dan σ=1 dengan variabel acak Y berdistribusi Chi square dengan derajat bebas sebesar υ yang mempunyai parameter α=υ/2 dan β=2. 28 υ Y X
- 29.
- 30. Distribusi Lognormal Parameter µ dan σ Probability Density Function, f(x) Cummulative Distribution Function, F(x) 30 > = −− other x x e xf x 0 0 .2.)( 2 )2/())(ln( 22 σπ σµ f(x) F(x) > ≤ = ∫ 0)( 00 )( 0 xdiif x xF x
- 31. Distribusi Lognormal Parameter µ dan σ Mean Variance 31 2/2 σµ µ + = e )1( 22 22 −= + σσµ σ ee
- 32. Distribusi Lognormal Hubungan DistribusiLognormal dengan Distribusi Normal Jika X adalah variabel acak independen berdistribusi Normal (µ,σ), maka eX adalah variabel acak berdistribusi Lognormal 32
- 33. Distribusi Chi-Square Parameter υ (degree of freedom) Probability Density Function, f(x) Cummulative Distribution Function, F(x) 33 f(x) F(x) > ≤ = ∫ 0)( 00 )( 0 xdiif x xF x > Γ= −−− other x ex xf x 0 0 )( 2 )( 2 2/1)2/(2/ υ υυ
- 34. Distribusi Chi-Square Dinotasikan denganCHISQR(x;υ) atau χ2 Parameter υ (degree of freedom) Mean Variance 34 υµ = υσ 22 =
- 35. Distribusi Chi-Square Hubungan DistribusiChi Square dengan Distribusi Normal Jika X adalah variabel acak independen berdistribusi Normal (µ,σ) dengan derajat kebebasan sebesar υ, maka X2 adalah variabel acak berdistribusi Chi Square 35
- 36. Distribusi Chi-Square Hubungan DistribusiChi Square dengan Distribusi Gamma Jika X adalah variabel acak independen berdistribusi Chi Square dengan parameter υ, maka akan ekuivalen dengan variabel acak berdistribusi Gamma (α, β) dengan parameter α=υ/2 dan β=2 36
- 37.
- 38. Distribusi F Hubungan DistribusiF dengan Distribusi Chi Square Jika X1 dan X2 adalah variabel acak independen berdistribusi Chi-Square dengan derajat kebebasan sebesar υ1 dan υ2, maka rasio X1 dan X2 adalah variabel acak berdistribusi F 38 2 2 1 1 υ υ X X F =
- 39.
- 40.
- 41.
- 42. 42 Terima kasih ...Terimakasih ... ... Ada pertanyaan ???... Ada pertanyaan ???