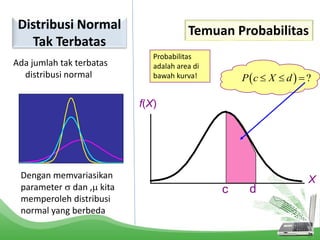
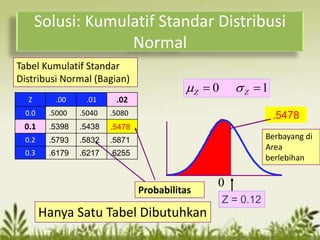
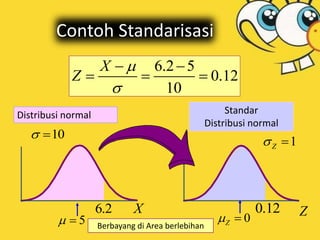
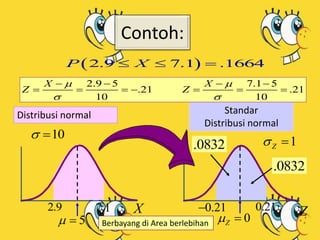
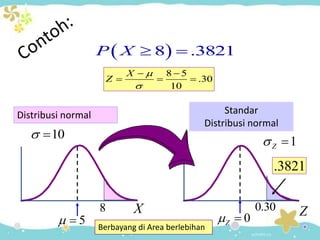
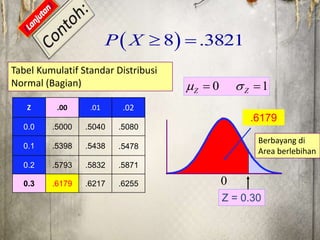
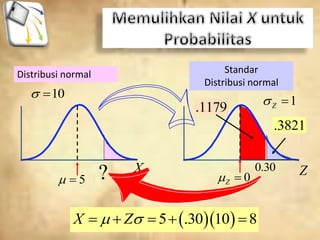
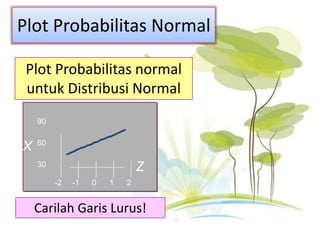
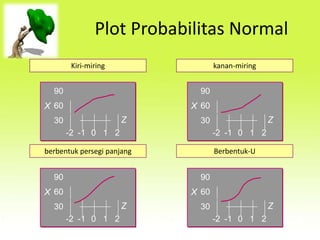
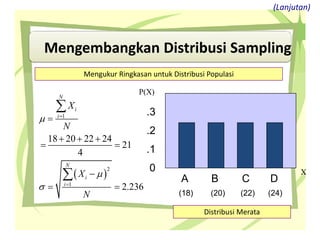
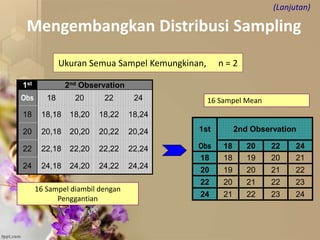
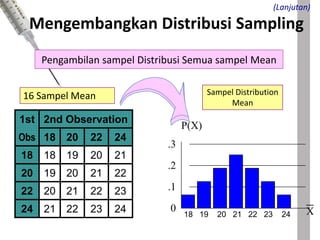
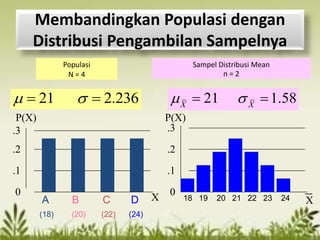
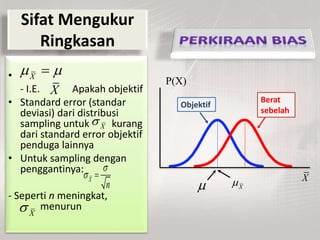
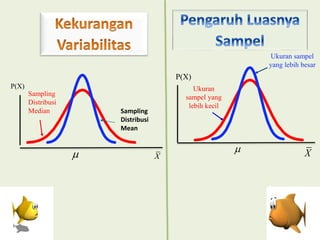
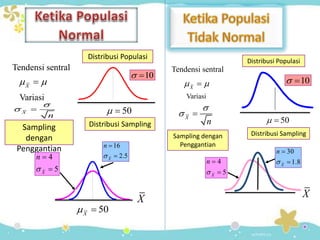
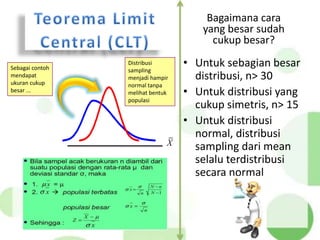
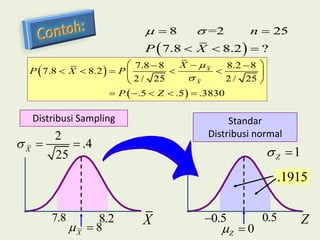
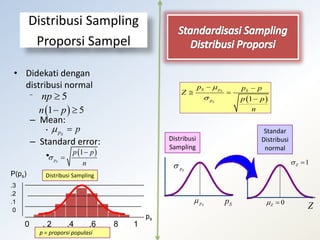
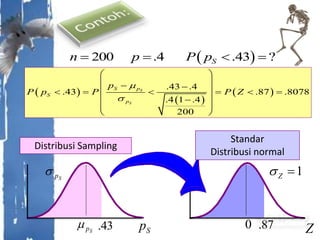
Dokumen tersebut membahas tentang distribusi normal dan distribusi sampling. Distribusi normal merupakan distribusi probabilitas kontinu yang paling penting dalam statistika yang memiliki bentuk lonceng simetris. Distribusi sampling adalah distribusi probabilitas dari statistik sampel sebagai variabel acaknya yang digunakan untuk memperkirakan parameter populasi berdasarkan sampel.