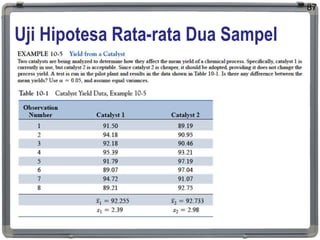
Teks tersebut membahas tentang statistika inferensia yang menganalisis atau mensintesa data untuk menggeneralisasi sampel terhadap populasi, mengestimasi parameter, menguji hipotesa, dan membuat prediksi untuk menghasilkan informasi dan kesimpulan. Metode pengujian hipotesa secara statistik digunakan untuk membentuk kesimpulan mengenai populasi berdasarkan sampel yang diambil.





































































































![Uji Hipotesa Rata-Rata dgn MatLab
Single sample 2 known
[h,p] = ztest(Datavector,0,,,tail)
Single sample 2 unknown
[h,p] = ttest(Datavector,0,,tail)
104](https://image.slidesharecdn.com/sinf202002-210811090319/85/Modul-Ajar-Statistika-Inferensia-ke-2-Uji-Hipotesa-Rata-rata-Parametrik-104-320.jpg)
