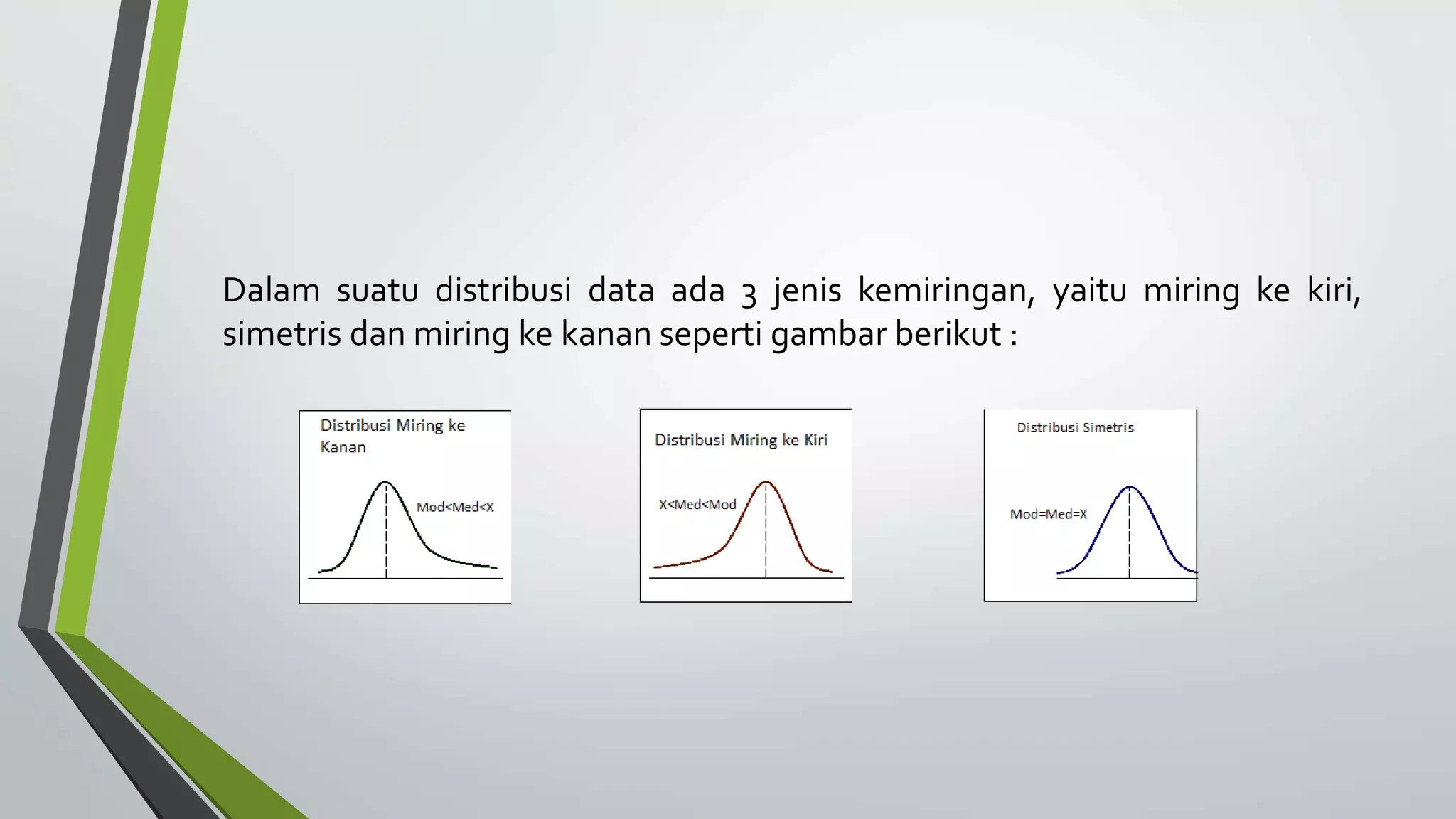
Distribusi normal, atau distribusi Gauss, adalah distribusi probabilitas penting yang sering digunakan sebagai model untuk data riil di berbagai bidang, termasuk karakteristik fisik, pengukuran kesalahan, dan indikator ekonomi. Ciri-ciri distribusi normal meliputi kurva simetris, uni-modal, serta mean, median, dan modus yang terletak pada satu titik. Sifat-sifat lainnya mencakup adanya karakteristik matematis tertentu, seperti total luas di bawah kurva yang sama dengan 1 dan proporsi data yang terdistribusi dalam interval tertentu berdasarkan jarak dari rata-rata.

1. DISTRIBUSI NORMAL
Kelompok 8 :
Ulfia Perdani
Rahmania Desri
Rachmi Restuti Arynda

2. DISTRIBUSI NORMAL
• Distribusi Normal (Distribusi Gauss)  merupakan distribusi probabilitas
yang paling penting baik dalam teori maupun aplikasi statistik.
• Terminology “normal”  karena memang distribusi ini adalah yang paling banyak
digunakan sebagai model bagi data riil di berbagai bidang, seperti :
• Karakteristik fisik mahluk hidup (berat, tinggi badan manusia, hewan dll)
• Kesalahan-kesalahan pengukuran dalam eksperimen ilmiah pengukuran-pengukuran
intelejensia dan perilaku
• Nilai skor berbagai pengujian dan berbagai ukuran dan indikator ekonomi.

3. Contoh lain variabel random yg memiliki distribusi normal misalnya:
• Distribusi error dalam pengukuran
• Pengukuran dalam meteorologi
• Pengukuran curah hujan
• Sebagai pendekatan bagi distribusi binomial
dan distribusi hipergeometrik, dan lainnya

4. Kenapa penting?
• Distribusi normal terjadi secara alamiah. Seperti diuraikan sebelumnya banyak
peristiwa di dunia nyata yang terdistribusi secara normal.
• Beberapa variable acak yang tidak terdistribusi secara normal dapat dengan
mudah ditranformasikan menjadi suatu distribusi variabel acak yang normal.
• Banyak hasil dan teknik analisis yang berguna dalam pekerjaan statistik hanya bisa
berfungsi dengan benar jika model distribusinya berupa distribusi normal
• Ada beberapa variabel acak yang tidak menunjukkan distribusi normal pada
populasinya Namun distribusi rata-rata sampel yang diambil secara random dari
populasi tersebut ternyata menunjukkan distribusi normal.

5. Ciri-ciri Distribusi Normal
Disusun dari variable random kontinu
Kurva distribusi normal mempunyai satu
puncak (uni-modal)
Kurva berbentuk simetris dan menyerupai
lonceng hingga mean, median dan modus
terletak pada satu titik.
Kurva normal dibentuk dengan N yang tak
terhingga.
Peristiwa yang dimiliki tetap independen.
Ekor kurva mendekati absis pada
penyimpangan 3 SD ke kanan dan ke kiri dari
rata-rata dan ekor grafik dapat dikembangkan
sampai tak terhingga tanpa menyentuh sumbu
absis.

6. Sifat Distribusi Normal
Sifat-Sifat Distribusi Normal:
1.Rata-ratanya (mean) μ dan standard deviasinya = σ
2.Mode (maximum) terjadi di x=μ
3.Bentuknya simetrik thd x=μ
4.Titik belok tepat di x=μ±σ
5.Kurva mendekati nol secara asimptotis semakin x jauh dari x=μ
6.Total luasnya = 1

7. Distribusi Normal : Sifat
Bentuk distribusi normal ditentukan oleh μ dan σ.
1
2
μ1 = μ2 σ1 > σ2
1
2
1
2
μ1 < μ2 σ1 < σ2
μ1 < μ2 σ1 = σ2

8. Distribusi Normal
8
• Variabel random X berdistribusi normal, dengan mean dan
variansi mempunyai fungsi densitas
• F(x), hanya bisa ditentukan dari integrasi secara numerik,
karena persamaan tersebut tidak bisa diintegrasi secara
analitik.
)2()x( 22
e
2
1
),;x(n 


 x

9. • luas daerah di bawah kurva dinyatakan dengan :
)xXx(P 21 




2
1
222
1
x
x
)2()x(
x
x
21 dxe
2
1
dx),;x(n)xXx(P
1dxe
2
1
)X(P )2()x( 22


 



X1
x
X2

10. Untuk setiap distribusi populasi dari suatu variabel acak yang mengikut
sebuah distribusi normal, maka
• 68,26% dari nilai-nilai variabel berada dalam ± 1 x dari x ,
• 95,46% dari nilai-nilai variabel berada dalam ± 2 x dari x ,
• 99,73% dari nilai-nilai variabel berada dalam ± 3 x dari x 

11. Gambar hubungan antara luasan dan
N(,2)

12. Distribusi Normal Standar (1)



x
Z
 




 2
1
2
1
22
1
2 z
z
z
z
z
2
1z
z
z
2
1
21 dz)1,0;z(ndze
2
1
dze
2
1
)zZz(P
ternyata substitusi
menyebabkan distribusi normal
menjadi , yang disebut distribusi normal standar.



x
Z
),;z(n 
)1,0;z(n
• apabila variabel X ditransformasikan dengan
substitusi
maka :

13. Dalam suatu distribusi data ada 3 jenis kemiringan, yaitu miring ke kiri,
simetris dan miring ke kanan seperti gambar berikut :