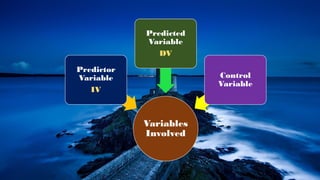
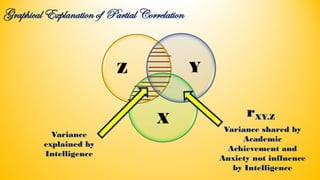
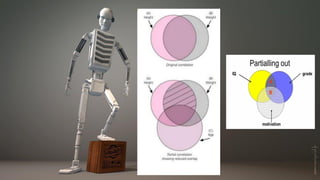
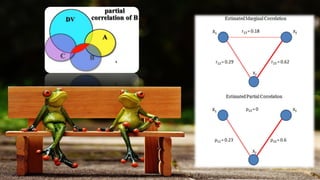
Partial correlation is a statistical method used to measure the strength and direction of a linear relationship between two continuous variables while controlling for one or more other variables, known as covariates. It eliminates the effects of confounding variables to reveal the true relationship between the primary variables. The document also includes assumptions for conducting partial correlation and provides illustrative examples detailing calculations and interpretations.

1. Partial Correlation
K.THIYAGU, Assistant Professor, Department of Education, Central University of Kerala, Kasaragod

2. Partial Correlation
Partial Correlation measures the
Correlation between X and Y
Controlling for Z
Partial correlation is a measure of
the strength and direction of a
linear relationship between
two continuous variables
whilst
controlling for the effect of one or
more other continuous variables
(also known as 'covariates' or
'control' variables).

3. We can
take out / eliminate / keep constant
the effect of third variable
(confound variable)
by using a statistical technique
called
Partial Correlation.
The effect or contribution
of third factor is
Partial out
from the correlation
between other two factors,
this technique is called
Partial correlation.

4. Variables
Involved
Predictor
Variable
IV
Predicted
Variable
DV
Control
Variable

5. Anxiety
X
Academic
Achievement
Y
Intelligence
Z
rAcademic Ahivement (Y) Anxiety (X) . Intelligence (Z)
Correlation can be represented as

6. Z
X
Y
Variance
explained by
Intelligence
Variance shared by
Academic
Achievement and
Anxiety not influence
by Intelligence
Graphical Explanation of Partial Correlation
rXY.Z

10. Note the subscripts in the symbol for a
partial correlation coefficient:
rxy●z
which indicates that the correlation coefficient is for X
and Y controlling for Z

11. •One (dependent) variable and One (independent)
variable and these are both measured on a
Continuous Scale
Assumption # 1
• One or more control variables, also known as
covariates measured on continuous scaleAssumption # 2
•A linear relationship between all three variables.Assumption # 3
•No significant outliers.Assumption # 4
•Variables should be approximately normally
distributedAssumption # 5

12. Partial Correlation - Example
The table lists
husbands’ hours of
housework per week
(Y), number of
children (X), and
husbands’ years of
education (Z) for a
sample of 12 dual-
career households

13. • A correlation matrix appears below
• The bivariate (zero-order) correlation between husbands’ housework and
number of children is +0.50
• This indicates a positive relationship
Partial Correlation - Example

14. Calculating the partial (first-order) correlation between husbands’ housework
and number of children controlling for husbands’ years of education yields +0.43
Partial Correlation - Example

15. Interpretation
• Comparing the bivariate correlation (+0.50) to the partial
correlation (+0.43) finds little change
• The relationship between number of children and husbands’
housework controlling for husbands’ education has not changed
• Therefore, we have evidence of a direct relationship
Partial Correlation - Example

16. Correlation
Partial Correlation
The effect of the third
variable (Z) is partialled
out from BOTH the
variables (X & Y)
Semi Partial Correlation
The effect of third
variable (Z) was
partialled out from only
one variable (X & Y) and
NOT from both the
variables

18. From the following data, calculate the correlation coefficient between
variable I and II by keeping the effect of variable III constant.
r12=0.6 ; r13=0.5; r23=0.3

19. Thank
You
K.THIYAGU, Assistant
Professor, Department of Education,
Central University of Kerala, Kasaragod