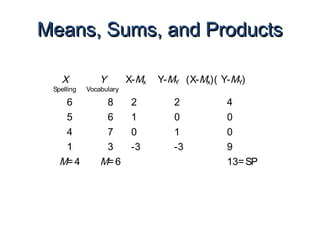
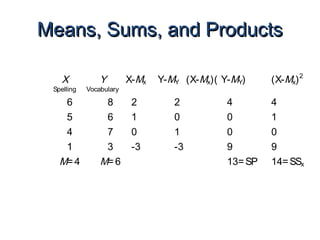
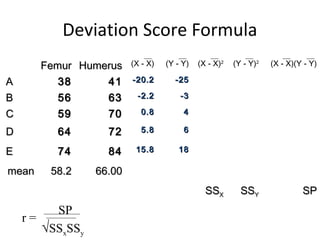
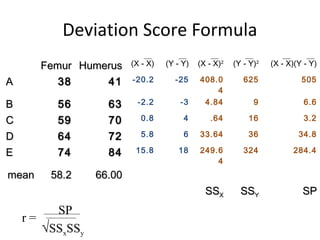
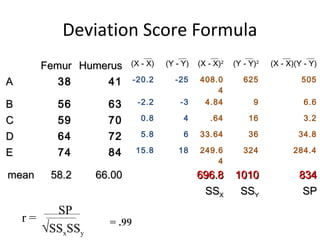
This document provides an overview of correlation, including: - Correlation measures the degree of linear relationship between two variables from -1 to 1. - It can be positive, negative, or zero. A stronger correlation is closer to -1 or 1. - Calculating correlation involves determining sums, means, and deviations of the variables to plug into the correlation formula. - The example calculates a correlation coefficient of 0.75 between reading readiness and achievement scores, indicating a strong positive linear relationship.

1. Chapter 12

2. Correlation

3. Correlation - Definition
Correlation: a statistical technique that measures and describes
the degree of linear relationship between two variables
Obs X Y
A 1 1
B 1 3
C 3 2
D 4 5
E 6 4
F 7 5
Dataset
X
Y
Scatterplot

4. Characteristics
• Direction
– Positive (+) or Negative (-)
• Degree of association
– Between –1 and 1
– Absolute values signify strength
• Form
– Linear or Non-linear
– We will work with linear only

5. Direction
Positive
Large values of X associated
with large values of Y,
small values of X associated
with small values of Y.
e.g. IQ and SAT
Large values of X associated
with small values of Y
& vice versa
e.g. SPEED and ACCURACY
Negative

6. Degree of association
• If the points do not fall along a straight line, then there is NO
linear association.
• If the points fall nearly along a straight line, then there is a
STRONG linear association.
• If the points fall exactly along a straight line, then there is a
PERFECT linear association.
Strong
(tight cloud)
Weak
(diffuse cloud)

8. Practice
• Which value represents the strongest
relationship?
1. .56
2. -.32
3. .24
4. -.77

9. Practice
• Which value represents the weakest
relationship?
1. .56
2. -.32
3. .24
4. -.77

10. Practice
• Which value represents the strongest
relationship?
1. .89
2. .22
3. -.66
4. -.15

11. Practice
• The older we get, the less sleep we tend to
require. What is the nature of this
relationship?
1. Positive relationship
2. Negative relationship

12. Practice
• The more education we receive, the higher
our salary when we enter the workforce.
What is the nature of this relationship?
1. Positive relationship
2. Negative relationship

13. Practice
• The better an employees feels about his or
her job, the less often they will call in sick.
What is the nature of this relationship?
1. Positive relationship
2. Negative relationship

14. Types of Correlations
• For interval/ratio data use Pearson’s r
• For ordinal data use Spearman’s r
• For nominal data use the phi coefficent

15. Pearson’s r
• One way to calculate the correlation is to use
Pearson’s r
• Can use a Deviation score formula
– r is a fraction that captures
– where
Covariation of X and YCovariation of X and Y
Variation of X and YVariation of X and Y
separatelyseparately
r =
SP
√SSxSSy
SP = Σ (X - X)(Y - Y)

16. Deviation Score Formula
FemurFemur HumerusHumerus (X - X) (Y - Y) (X - X)2
(Y - Y)2
(X - X)(Y - Y)
AA 3838 4141
BB 5656 6363
CC 5959 7070
DD 6464 7272
EE 7474 8484
meanmean 58.258.2 66.0066.00
SSSSXX SSSSYY SPSP
r =
SP
√SSxSSy

17. Deviation Score Formula
FemurFemur HumerusHumerus (X - X) (Y - Y) (X - X)2
(Y - Y)2
(X - X)(Y - Y)
AA 3838 4141 -20.2-20.2 -25-25
BB 5656 6363 -2.2-2.2 -3-3
CC 5959 7070 0.80.8 44
DD 6464 7272 5.85.8 66
EE 7474 8484 15.815.8 1818
meanmean 58.258.2 66.0066.00
SSSSXX SSSSYY SPSP
r =
SP
√SSxSSy

18. Deviation Score Formula
FemurFemur HumerusHumerus (X - X) (Y - Y) (X - X)2
(Y - Y)2
(X - X)(Y - Y)
AA 3838 4141 -20.2 -25 408.0
4
625 505
BB 5656 6363 -2.2 -3 4.84 9 6.6
CC 5959 7070 0.8 4 .64 16 3.2
DD 6464 7272 5.8 6 33.64 36 34.8
EE 7474 8484 15.8 18 249.6
4
324 284.4
meanmean 58.258.2 66.0066.00
SSSSXX SSSSYY SPSP
r =
SP
√SSxSSy

19. Deviation Score Formula
FemurFemur HumerusHumerus (X - X) (Y - Y) (X - X)2
(Y - Y)2
(X - X)(Y - Y)
AA 38 41 -20.2 -25 408.0
4
625 505
BB 56 63 -2.2 -3 4.84 9 6.6
CC 59 70 0.8 4 .64 16 3.2
DD 64 72 5.8 6 33.64 36 34.8
EE 74 84 15.8 18 249.6
4
324 284.4
meanmean 58.258.2 66.0066.00 696.8696.8 10101010 834834
SSSSXX SSSSYY SPSP
r =
SP
√SSxSSy
= .99

20. The Computational Formula
( )( )
( )[ ] ( )[ ]∑ ∑∑ ∑
∑∑ ∑
−−
−
=
2222
YYnXXn
YXXYn
r

21. What are the preliminary steps to
calculating a correlation coefficient?
• When calculating the
correlation coefficient, one
begins with scores on two
variables.

22. What are the preliminary steps to
calculating a correlation coefficient?
• When calculating the
correlation coefficient, one
begins with scores on two
variables.
• The illustration on the right
involves scores on a reading
readiness test, and scores later
obtained by these same
students on a reading
achievement test.
Reading
Readiness
Scores
Reading
Achievement
Scores
Todd 10 19
Andrea 16 25
Kristen 19 23
Luis 22 31
Scott 28 27

23. What are the preliminary steps to
calculating a correlation coefficient?
• The formula used in the
calculation involves six
different values obtained
from the X and Y variables
The first two values are simply
the sum of X values and Y
values. Those sums are 95
and 125 for these particular
test scores.
X
Reading
Readiness
Scores
Y
Reading
Achievement
Scores
Todd 10 19
Andrea 16 25
Kristen 19 23
Luis 22 31
Scott 28 27

24. What are the preliminary steps to
calculating a correlation coefficient?
• The formula used in the
calculation involves six
different values obtained
from the X and Y variables
• The first two values are
simply the sum of X values
and Y values. Those sums
are 95 and 125 for these
particular test scores.
X
Reading
Readiness
Scores
Y
Reading
Achievement
Scores
Todd 10 19
Andrea 16 25
Kristen 19 23
Luis 22 31
Scott 28 27
95 125
∑
∑
=
=
125
95
Y
X

25. What are the preliminary steps to
calculating a correlation coefficient?
• The next step involves
squaring each of the X
and Y values.
X Y
10 19
16 25
19 23
22 31
28 27
95 125

26. What are the preliminary steps to
calculating a correlation coefficient?
• The next step involves
squaring each of the X
and Y values.
• and then summing
them
X2
X Y Y2
100 10 19 361
256 16 25 625
361 19 23 529
484 22 31 961
784 28 27 729
1985 95 125 3205

27. What are the preliminary steps to
calculating a correlation coefficient?
• Using the summation notation…
X2
X Y Y2
100 10 19 361
256 16 25 625
361 19 23 529
484 22 31 961
784 28 27 729
1985 95 125 3205
∑
∑
∑
∑
=
=
=
=
3205
1985
125
95
2
2
Y
X
Y
X

28. What are the preliminary steps to
calculating a correlation coefficient?
• In the next step, the
product of each pair of X
and Y scores is obtained.
X2
X Y Y2
100 10 19 361
256 16 25 625
361 19 23 529
484 22 31 961
784 28 27 729
1985 95 125 3205

29. What are the preliminary steps to
calculating a correlation coefficient?
• In the next step, the
product of each pair of X
and Y scores is obtained.
• and then summed.
X2
X XY Y Y2
100 10 190 19 361
256 16 400 25 625
361 19 437 23 529
484 22 682 31 961
784 28 756 27 729
1985 95 2465 125 3205

30. What are the preliminary steps to
calculating a correlation coefficient?
• Using the summation notation…
X2
X XY Y Y2
100 10 190 19 361
256 16 400 25 625
361 19 437 23 529
484 22 682 31 961
784 28 756 27 729
1985 95 2465 125 3205
∑
∑
∑
∑
∑
=
=
=
=
=
2465
3205
1985
125
95
2
2
XY
Y
X
Y
X

31. What are the preliminary steps to
calculating a correlation coefficient?
• The last of the
preliminary steps is to
simply determine the
number of people
being included in the
calculations. In this
case, the calculations
involve 5 students.
Therefore...
X2
X XY Y Y2
100 10 190 19 361
256 16 400 25 625
361 19 437 23 529
484 22 682 31 961
784 28 756 27 729
1985 95 2465 125 3205

32. What are the preliminary steps to
calculating a correlation coefficient?
• The last of the
preliminary steps is to
simply determine the
number of people
being included in the
calculations. In this
case, the calculations
involve 5 students.
Therefore...
X2
X XY Y Y2
100 10 190 19 361
256 16 400 25 625
361 19 437 23 529
484 22 682 31 961
784 28 756 27 729
1985 95 2465 125 3205
5=n

33. What are the preliminary steps to
calculating a correlation coefficient?
• In summary, our six values
used to calculate the
correlation coefficient are…
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n
X2
X XY Y Y2
100 10 190 19 361
256 16 400 25 625
361 19 437 23 529
484 22 682 31 961
784 28 756 27 729
1985 95 2465 125 3205

34. Using the computational formula...
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n

35. Using the computational formula...
A somewhatA somewhat
impressive lookingimpressive looking
formula uses theseformula uses these
six values tosix values to
compute thecompute the
correlationcorrelation
coefficient...coefficient...
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n

36. A somewhatA somewhat
impressive lookingimpressive looking
formula uses theseformula uses these
six values tosix values to
compute thecompute the
correlationcorrelation
coefficient…,coefficient…,
however the formulahowever the formula
turns out not to beturns out not to be
very difficult to use.very difficult to use.
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n
Using the computational formula...

37. ( )( )
( )[ ] ( )[ ]∑ ∑∑ ∑
∑∑ ∑
−−
−
=
2222
YYnXXn
YXXYn
r
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n
The formula is...The formula is...
Using the computational formula...

38. ( )( )
( )[ ] ( )[ ]∑ ∑∑ ∑
∑∑ ∑
−−
−
=
2222
YYnXXn
YXXYn
r
∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n
The variables in thisThe variables in this
formula consist of onlyformula consist of only
the six previouslythe six previously
calculated values to thecalculated values to the
left...left...
Using the computational formula...

39. ∑
∑
∑
∑
∑
=
=
=
=
=
=
2465
3205
1985
125
95
5
2
2
XY
Y
X
Y
X
n
Here is the formula withHere is the formula with
these values inserted...these values inserted...
Using the computational formula...
( )( )
( )[ ] ( )[ ]∑ ∑∑ ∑
∑∑ ∑
−−
−
=
2222
YYnXXn
YXXYn
r
( )( ) ( )( )
( )( ) ( )[ ]( )( ) ( )[ ]22
125320559519855
1259524655
−−
−
=r

40. The correlation between these students readingThe correlation between these students reading
readiness scores and later reading achievementreadiness scores and later reading achievement
scores is 0.75scores is 0.75
X
Reading
Readiness
Scores
Y
Reading
Achievement
Scores
Todd 10 19
Andrea 16 25
Kristen 19 23
Luis 22 31
Scott 28 27
Using the computational formula…

41. Determining Significance
►Test whether the association is greater than can be
expected by chance
►Hypotheses
– H0: ρ = 0
– H1: ρ ≠ 0
►df = n – 2
– n is the total number of subjects
►Use the Pearson correlation table
►If your correlation score is greater than the score given
in the table (critical value), then your correlation is
significant

42. Now its your turn...

43. Now its your turn...
• To the right are the
scores of four students
on a spelling test and a
vocabulary test. Can you
calculate the correlation
coefficient?
X
Spelling
Y
Vocabulary
Sandra 8 10
Neil 5 6
Laura 4 7
Jerome 1 3

44. Now its your turn...
• On your own paper,
calculate these six values:
∑
∑
∑
∑
∑
=
=
=
=
=
=
XY
Y
X
Y
X
n
2
2
X
Spelling
Y
Vocabulary
Sandra 8 10
Neil 5 6
Laura 4 7
Jerome 1 3

45. Now its your turn...
• You should get these
values:
141
194
106
26
18
4
2
2
∑
∑
∑
∑
∑
=
=
=
=
=
=
XY
Y
X
Y
X
n X2
X XY Y Y2
64 8 80 10 100
25 5 30 6 36
16 4 28 7 49
1 1 3 3 9
106 18 141 26 194

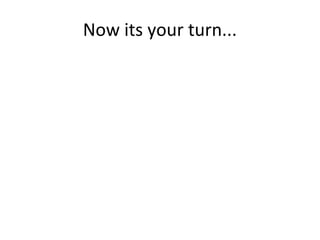
46. Now its your turn...
• Now insert these values
in the equation
141
194
106
26
18
4
2
2
∑
∑
∑
∑
∑
=
=
=
=
=
=
XY
Y
X
Y
X
n
( )( )
( )[ ] ( )[ ]∑ ∑∑ ∑
∑∑ ∑
−−
−
=
2222
YYnXXn
YXXYn
r
( )( ) ( )( )
( )( ) ( )[ ]( )( ) ( )[ ]22
261944181064
26181414
−−
−
=r
96.0
100
96
==r

47. Significant at alpha = .05?
►What is the critical value?
1. .95
2. .90
3. .811
4. .632

48. Significant?
►Is this correlation significant?
1.Yes
2.No

49. Regression

50. The Linear Equation
• If two variables are linearly related it is
possible to develop a simple equation to
represent the relationship
• E.g. centigrade to Fahrenheit:
–F = 1.8C + 32
– this formula gives a specific straight line

51. The Linear Equation
• Equation of the line (Y = bX + a)
– a and b are constants in a given line;
– X and Y change
Predictor
Criterion

52. The Linear Equation
• Equation of the line (Y = bX + a)
– The slope (b)
• the amount of change in y with one unit change in x
• On a graph, it is represented by how steep the line is.

53. The Linear Equation
• When b changes (different formulas)
Predictor
Criterion

54. The Linear Equation
• Equation of the line (Y = bX + a)
– The intercept (a)
• the value of y when x is zero
• On a graph, it is represented by where the line crosses
the y axis

55. The Linear Equation
• When a changes (different formulas)
Predictor
Criterion

56. Practice
• Y = 32(.3) + 10
• Identify the slope
1. 32
2. .3
3. 10

57. Practice
• Y = 32(.3) + 10
• Identify the Y intercept
1. 32
2. .3
3. 10

58. The Regression Line
• Relationships are rarely perfect. Scores are
“scattered”.
• The regression line is a straight line which is
drawn through a scatterplot, to summarize
the relationship between X and Y
• It is the line that minimizes the squared
deviations (Y – Y’)2
• We call these vertical deviations “residuals”

59. When there is some linear association, the
regression line fits as close to the points as possible
150
175
200
225
250
67 68 69 70 71 72 73 74 75 76 77
Weight
in
Pounds
Height in Inches
The 2001 Mets

60. Calculating the regression lineCalculating the regression line
► To the right are theTo the right are the
scores of four studentsscores of four students
on a spelling test and aon a spelling test and a
vocabulary test.vocabulary test.
► Sallie has just takenSallie has just taken
the spelling test andthe spelling test and
scored a 6. What doscored a 6. What do
you predict heryou predict her
vocabulary score tovocabulary score to
be?be?
X
Spelling
Y
Vocabulary
Sandra 6 8
Neil 5 6
Laura 4 7
Jerome 1 3

61. Means, Sums, and Products
X
Spelling
Y
Vocabulary
6 8
5 6
4 7
1 3
M=4 M=6

62. Means, Sums, and ProductsMeans, Sums, and Products
X
Spelling
Y
Vocabulary
X-Mx Y-MY
6 8 2 2
5 6 1 0
4 7 0 1
1 3 -3 -3
M=4 M=6

63. Means, Sums, and ProductsMeans, Sums, and Products
X
Spelling
Y
Vocabulary
X-Mx Y-MY (X-Mx)( Y-MY)
6 8 2 2 4
5 6 1 0 0
4 7 0 1 0
1 3 -3 -3 9
M=4 M=6 13=SP

64. Means, Sums, and ProductsMeans, Sums, and Products
X
Spelling
Y
Vocabulary
X-Mx Y-MY (X-Mx)( Y-MY) (X-Mx)2
6 8 2 2 4 4
5 6 1 0 0 1
4 7 0 1 0 0
1 3 -3 -3 9 9
M=4 M=6 13=SP 14=SSx

65. Now the formulasNow the formulas
X
Spelling
Y
Vocabulary
X-Mx Y-MY (X-Mx)( Y-MY) (X-Mx)2
6 8 2 2 4 4
5 6 1 0 0 1
4 7 0 1 0 0
1 3 -3 -3 9 9
M=4 M=6 13=SP 14=SSx
93.
14
13
===
xSS
SP
b 28.2)4(93.6 =−=−= XY bMMa

66. Now the formulas
86.728.2)6(93.
^
=+=+= abXY
Sallie should get a vocabulary score of 7.86

67. Causation
• A strong relationship between variables does
not always mean that changes in one variable
cause changes in the other variable.

68. Causation
• The relationship between two variables is
often influenced by other variables lurking in
the background.
“Beware the lurking variable!

69. Causation
• The best evidence of causation comes from
randomized comparative experiments.

70. The Chi-Square Analysis

71. Chi-Square
• Examines nominal data or ordinal data that is
being treated as a category
• Called a non-parametric test
– Chi-square requires no assumptions about the
shape of the population distribution from which a
sample is drawn.
• The test examines the difference between
observed counts and expected values

72. Chi-square Goodness of Fit
• Two ways to use the chi-square
• First way to use the chi-square is called the
Goodness of Fit test
– Determines whether a frequency distribution
follows a claimed distribution
• Hypothesis test
– Ho: the variable follows the claimed distribution
– H1: the variable does not follow the claimed
distribution

73. Chi-square Goodness of Fit
• The FBI compiles data on
crime and crime rates and
publishes the information
in Crime in the United
States. A violent crime is
classified by the FBI as
murder, forcible rape,
robbery, or aggravated
assault.
Types of
violent crime
Relative
frequency
Murder 0.012
Forcible rape 0.054
Robbery 0.323
Agg. assault 0.611
1.000
Types of
violent crime Frequency
Murder 9
Forcible rape 26
Robbery 144
Agg. assault 321
500
Crime Distribution for 1995
Last Year

74. Chi-square Goodness of Fit
• Do the data provide sufficient evidence to conclude that last
year’s distribution of violent crimes has changed from the
1995 distribution?
• Get expected frequency
E = Np
Types of
violent crime
Relative
frequency
p
Expected
frequency
Np =E
Murder 0.012 (500)(0.012) = 6.0
Forcible rape 0.054 (500)(0.054) = 27.0
Robbery 0.323 (500)(0.323) = 161.5
Agg, assault 0.611 (500)(0.611) = 305.5

75. Chi-square Goodness of Fit
• Then calculate the chi formula
Cell O E O-E (O-E)2
(O-E)2
/E
Murder 9 6 3 9 1.5
Forcible Rape 26 27 -1 1 0.037
Robbery 144 161.5 -17.5 306.25 1.896
Agg. Assault 321 305.5 15.5 240.25 0.786
χχ22
= 4.219= 4.219
( )
∑
−
=
E
EO
2
2
χ

76. Chi-square Goodness of Fit
• Finally
– Use Table to find critical value
– df = k – 1, where k is the number of cells
– Example – df = 3
– Critical value is 7.815
– Our value is 4.219 so fail to reject
– This means that the pattern of crime has not
changed when comparing 1995 to last year.

77. Chi-square Test of Independence
• Second way to use a chi-square is the test of
independence
– Hypotheses
• H0: Variables Are Independent
• Ha: Variables Are Related (Dependent)

78. Chi-square Test of Independence
• We are interested in whether single men vs.
women are more likely to own cats vs. dogs.
• Notice that both variables are categorical.
– Kind of pet: people are classified as owning cats or
dogs. We can count the number of people
belonging to each category
– Sex: people are male or female. We count the
number of people in each category

79. Chi-square Test of Independence
• Are these differences
because there is a real
relationship between
gender and pet
ownership?
• Or is there actually no
relationship between
these variables?
Cat Dog
Male 20 30 50
Female 30 20 50
50 50 100

80. Chi-square Test of Independence
• To answer this question, we need to know
what we would expect to observe if the null
hypothesis were true
• The differences between these expected
values and the observed values are
aggregated according to the Chi-square
formula

81. Chi-square Test of Independence
• To find expected value for a cell
of the table, multiply the
corresponding row total by the
column total, and divide by the
grand total
• For the first cell (and all other
cells), (50 x 50)/100 = 25
• Thus, if the two variables are
unrelated, we would expect to
observe 25 people in each cell
Cat Dog
Male 20 30 50
Female 30 20 50
50 50 100

82. Chi-square Test of Independence
• Then apply to the same chi-square formula
( )
∑
−
=
E
EO
2
2
χ
Cell O E O-E (O-E)2
(O-E)2
/E
Male w/ Car 20 25 -5 25 1
Male w/ Dog 30 25 5 25 1
Female w/ Cat 30 25 5 25 1
Female w/ Dog 20 25 -5 25 1
χχ22
= 4= 4

83. Chi-square Test of Independence
• Compare to critical value from chi-square table.
• Degrees of freedom is
– (number of rows – 1)(number of columns -1)
– In our example (2-1)(2-1)= 1
– Critical value is 3.841
– Our value of 4 is greater than the critical so reject the null.
Cat Dog
Male 20 30 50
Female 30 20 50
50 50 100