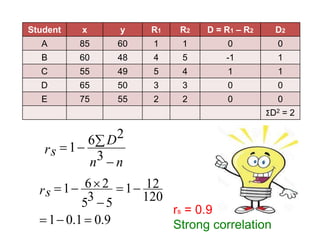
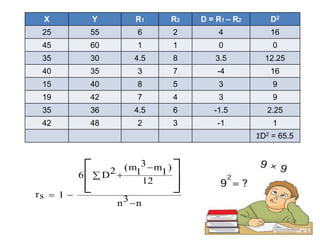
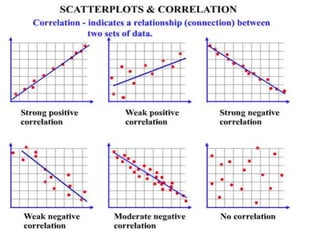
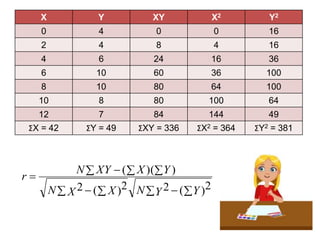
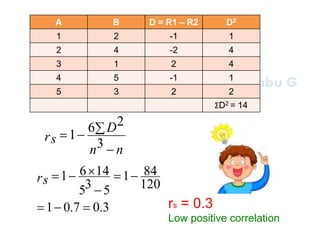
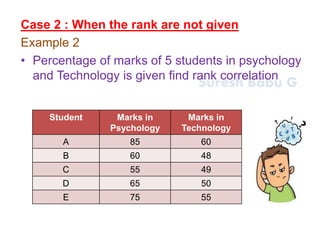
The document discusses correlation analysis and different types of correlation: 1. It defines correlation as measuring the relationship between two variables, and describes correlation as examining how two variables co-vary rather than being causative. 2. Positive correlation occurs when both variables increase or decrease together, while negative correlation is when one variable increases as the other decreases. 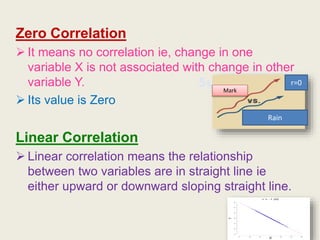3. Zero correlation means no relationship between the variables as change in one does not correspond to change in the other.

1. Suresh Babu G
Correlation Analysis
Suresh Babu G
Assistant Professor
CTE CPAS Paippad, Kottayam
If you study well you
can score more mark

2. Suresh Babu G
Correlation
 Correlation measures the relationship between
two variables.
 Correlation analysis is a means for examining
the relationship between two variables
systematically.
 Correlation studies and measures the direction
and intensity of relationship among variables.
 It measures co-variation, not causation.
 Correlation is denotes as “r”
A+

3. Suresh Babu G
Types of Correlation
Positive Correlation
When the increase in one variable X is followed
by a corresponding increase in another variable
Y and when X decreases the Y deceases, the
correlation is said to be positive.
It ranges from 0 to +1
Example : More you learn you can fetch more
mark.
When two variables ie, X and Y move in same
direction, it is positive correlation

4. Suresh Babu G
Negative Correlation
The increase in one variable X results in the
corresponding decrease in the other variable Y,
the correlation is said to be negative correlation.
It ranges from 0 to -1
Example : When you spend more time in
studying, chances of your failing decline.
When two variables ie, X and Y move in opposite direction,
it is negative correlation

5. Suresh Babu G
Zero Correlation
 It means no correlation ie, change in one
variable X is not associated with change in other
variable Y.
 Its value is Zero
Linear Correlation
 Linear correlation means the relationship
between two variables are in straight line ie
either upward or downward sloping straight line.
Mark
Rain
r=0

6. Suresh Babu G
Curvilinear Correlation
Curvilinear correlation means the relationship
between two variables are not in straight line ie
either upward or downward sloping curve.
Linear
Curvilinear

7. Suresh Babu G

8. Suresh Babu G

9. Suresh Babu G
Properties of Coefficient of
Correlation
• r has no units.
• A negative value of r indicates an
inverse relation.
• If r is positive the two variables
move in the same direction.
• The value of the correlation
coefficient lies between minus one
and plus one ( -1 ≤ r ≥ +1 )
• If r=0 the two variables are
uncorrelated.

10. Suresh Babu G
• If r = +1 or r = -1 the correlation is prefect.
• If the value is said to be high, when it is close to
+1 or -1.
• If the value is sais to be low, when it is close to
zero.
• The value of r is unaffected by the change of
origin and change of scale.
Properties of Coefficient of Correlation
It is important
learn it

11. Suresh Babu G
Karl Person’s Coefficient of
Correlation
It is also known as Product Moment
Correlation and Simple Correlation
Coefficient.
It gives a precise numerical value of the degree
of linear relationship between two variables X
and Y.
  
  

)2(2)2(2
))((
YYNXXN
YXXYN
r

12. Suresh Babu G
Example
 Calculate the Correlation Coefficient of the
following data.
No. of years of
schooling
Annual yield in
thousand
0 4
2 4
4 6
6 10
8 10
10 8
12 7

13. Suresh Babu G
X Y XY X2 Y2
0 4 0 0 16
2 4 8 4 16
4 6 24 16 36
6 10 60 36 100
8 10 80 64 100
10 8 80 100 64
12 7 84 144 49
ΣX = 42 ΣY = 49 ΣXY = 336 ΣX2 = 364 ΣY2 = 381
  
  

)2(2)2(2
))((
YYNXXN
YXXYN
r

14. Suresh Babu G
49238174223647
49423367

r
2401266717642548
20582352

r
266784
294r
644.0
4.456
294
3.1628
294 

r
r = 0.644
Positive Correlation

15. Suresh Babu G
Spearman’s Rank Correlation
 Spearman’s rank correlation was developed by
British psychologist C.E.Spearman.
 It is used when the variables cannot be
measured meaningfully ie, attributes.
 It is the Product Movement Correlation
between ranks.
nn
D
rs


3
26
1
Where
D = R1 –R2
R1 = Rank 1
R2 = Rank 2
n = Number of
pairs

16. Suresh Babu G
Case 1 : When Rank is Given
Example 1
• Rank given by two judges A and B of arts fest
are given. Find rank correlation.
Competitors
Judge 1 2 3 4 5
A 1 2 3 4 5
B 2 4 1 5 3

17. Suresh Babu G
A B D = R1 – R2 D2
1 2 -1 1
2 4 -2 4
3 1 2 4
4 5 -1 1
5 3 2 2
ΣD2 = 14
3.07.01
120
841
535
1461



rs
nn
D
rs


3
26
1
rs = 0.3
Low positive correlation

18. Suresh Babu G
Case 2 : When the rank are not given
Example 2
• Percentage of marks of 5 students in psychology
and Technology is given find rank correlation
Student Marks in
Psychology
Marks in
Technology
A 85 60
B 60 48
C 55 49
D 65 50
E 75 55

19. Suresh Babu G
Student x y R1 R2 D = R1 – R2 D2
A 85 60 1 1 0 0
B 60 48 4 5 -1 1
C 55 49 5 4 1 1
D 65 50 3 3 0 0
E 75 55 2 2 0 0
ΣD2 = 2
nn
D
rs


3
26
1
9.01.01
120
121
535
261



rs
rs = 0.9
Strong correlation

20. Suresh Babu G
Case 3 : When the ranks are repeated
Example 3
• The value of X and Y are given as
n3n
....
12
)2m3
2(m
12
)1m3
1(m2D6
1rs

 









X 25 45 35 40 15 19 35 42
Y 55 60 30 35 40 42 36 48
Where m1, m2, …. Are the
number of repetitions of ranks

21. Suresh Babu G
X Y R1 R2 D = R1 – R2 D2
25 55 6 2 4 16
45 60 1 1 0 0
35 30 4.5 8 3.5 12.25
40 35 3 7 -4 16
15 40 8 5 3 9
19 42 7 4 3 9
35 36 4.5 6 -1.5 2.25
42 48 2 3 -1 1
ΣD2 = 65.5
n3n
12
)1m3
1(m2D6
1rs










22. Suresh Babu G
35 occurs 2 times
so m1 = 2
883
12
232
5.656
1rs
















214.0786.01
504
396
1
504
5.05.656
1rs



 



rs = 0.214
Low positive correlation

23. Suresh Babu G