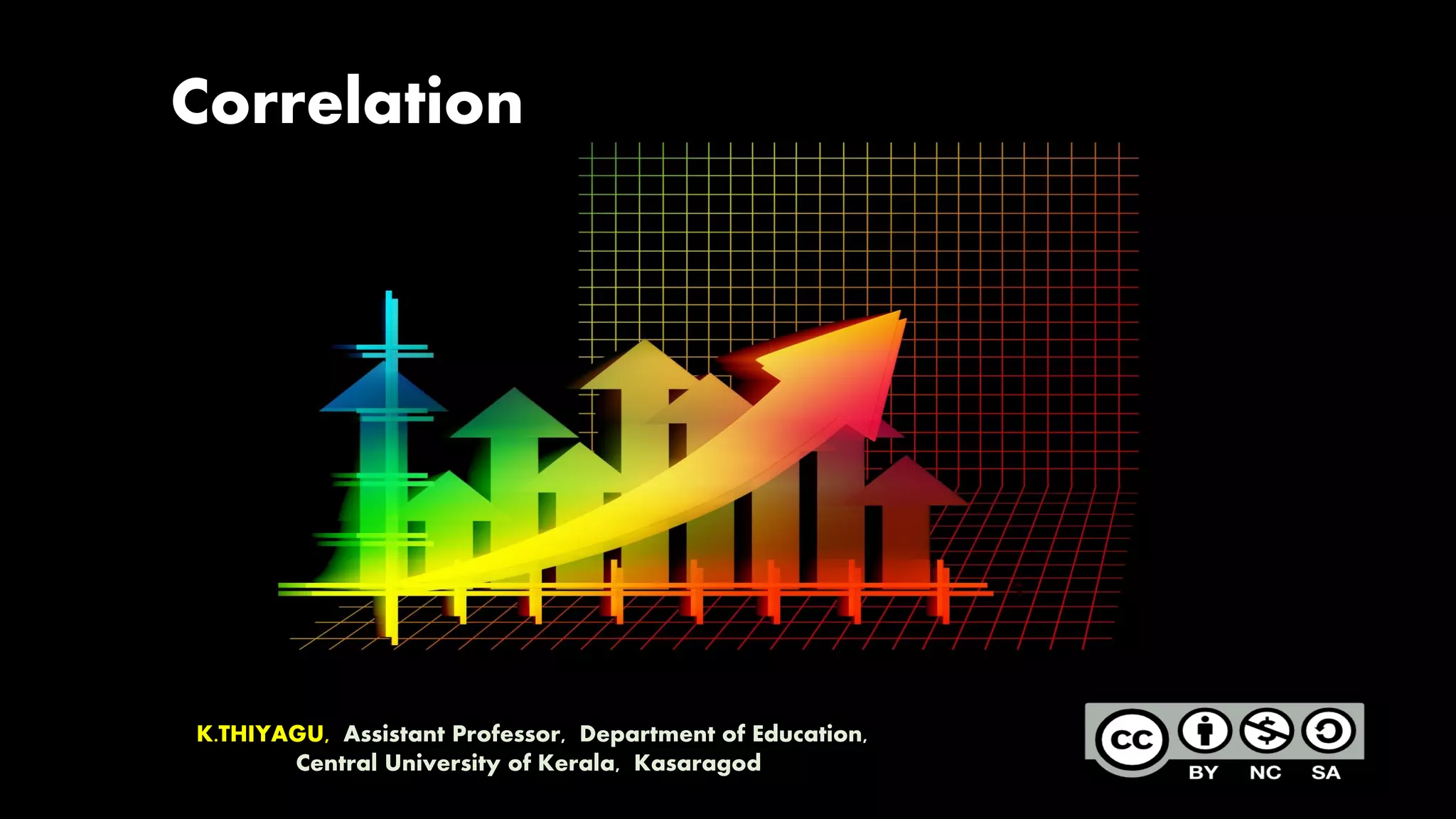
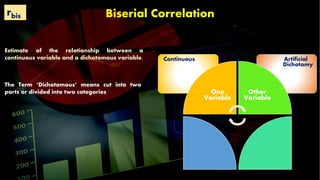
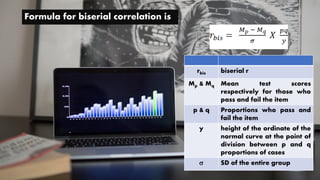
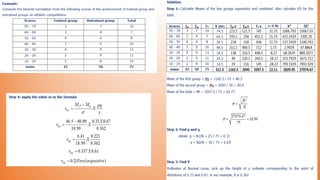
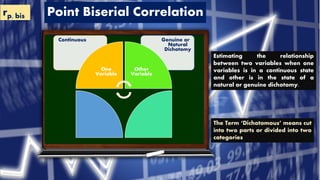
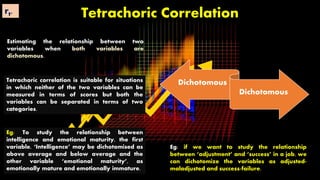
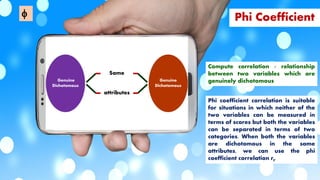
This document discusses various types of correlation coefficients used in statistics. It begins by describing Pearson's product-moment correlation coefficient (r) which measures the strength and direction of the linear relationship between two continuous variables. It then provides background on Karl Pearson who developed r. The rest of the document defines and provides formulas for other correlation coefficients including Spearman's rank correlation coefficient, point-biserial correlation, biserial correlation, tetrachoric correlation, and phi coefficient; and discusses their uses based on the scale types (nominal, ordinal, interval/ratio) of the variables.

1. Correlation
K.THIYAGU, Assistant Professor, Department of Education,
Central University of Kerala, Kasaragod

2. Pearson Product Moment Correlation
• PPMCC or PCC or Pearson’s r
• It is a measure of the strength of a
linear association between two
variables and is denoted by r.
• It is a measure of the
linear correlation between two
variables X and Y
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s.
Early work on the distribution of the sample correlation coefficient was carried out by Anil Kumar Gain
and R. A. Fisher from the University of Cambridge.

3. Born 27 March 1857, Islington, London, England
Died 27 April 1936 (aged 79), Surrey, England
Residence England
Nationality British
Known for Principal Component Analysis
Pearson distribution
Pearson's r
Pearson's chi-squared test
Phi coefficient
Academic
advisors
Francis Galton
Pearson with
Sir Francis Galton
Karl Pearson

4. Statistics is the grammer of science.
(Karl Pearson)

5. Pearson's correlation
coefficient is
the covariance of the
two variables divided
by the product of
their standard
deviations.
Pearson Product Moment Correlation Interpretation Correlation
Perfect Positive +1.0
Very high positive +0.90 to +0.99
High positive +0.70 to +0.90
Moderate positive +0.50 to +0.70
Low positive +0.30 to +0.50
Very low positive +0.10 to +0.30
Negligible positive +0.01 to +0.10
No correlation 0.0
Negligible negative - 0.01 to -0.10
Very low negative - 0.10 to -0.30
Low negative - 0.30 to -0.50
Moderate negative - 0.50 to -0.70
High negative - 0.70 to -0.90
Very high negative - 0.90 to -0.99
Perfect negative -1.0
InterpretationTable
2222
)()(
))((
YYNXXN
YXXYN
r
−−
−
=

7. • Correlation is used to describe the degree of relationship between
two variables.
• The reliability of test is calculated in terms of Pearson (r)
• The validity is estimated by the co-efficient of correlation (r)
• Item discrimination power is calculated by using Pearson’s ( r)
• Multiple correlation based on Pearson’s r
• Partial correlation employs the co-efficient of correlation ( r)
• Factor-analysis technique is the extension of Pearson’s r
• It predicts the depended variables on the basis of independent
variable
• Most of the personality theories are also developed by using this
correlation.
uses
of PPMCC

8. • It is a linear correlation. When the
two variables have the linear
distribution would yield accurate
co-efficient of correlation, but the
two variables are curve linearly
distributed, then the correlation of
co-efficient of two variables is not
dependable. This assumption is
taken into consideration while
using this technique.
• The distribution of scores of the
two variables should be normal. It
the distributions are skewed, it
would not yield dependable
correlation. The assumption is not
usually observed.
Disadvantages of PPMCC

9. Spearman’s
Rank-Difference Correlation

10. The Spearman’s Rank Correlation Coefficient is the
non-parametric statistical measure
used to study the
strength of association
between the
two ranked variables.
This method is applied to the ordinal set of numbers, which
can be arranged in order, i.e. one after the other so that
ranks can be given to each.
Spearman’s Rank Correlation
It was developed by Charles Spearman; this it is
called the Spearman rank correlation.
Spearman's rank correlation coefficient denoted
by the Greek letter  (rho)
It assesses how well the relationship
between two variables can be
described using a monotonic function.

11. Charles Edward Spearman
Born 10 September 1863,
London, United Kingdom
Died 17 September 1945 (aged 82),
London, United Kingdom
Known for g factor, Spearman's rank correlation
coefficient, factor analysis
Notable
students
Raymond Cattell, John C. Raven,
David Wechsler
Influences Francis Galton, Wilhelm Wundt

12. While Pearson's correlation assesses linear relationships,
Spearman's correlation assesses monotonic relationships
(whether linear or not).
A monotonic relationship is a relationship that does one of the
following: (1) as the value of one variable increases, so does
the value of the other variable; or (2) as the value of one
variable increases, the other variable value decreases
Monotonic Relationships

13. Monotonic relationships are where:
• One variable increases and the other increases.
Or,
• One variable decreases and the other decreases.
Monotonic variables increase (or decrease) in the same
direction, but not always at the same rate.
Linear variables increase (or decrease) in the same
direction at the same rate.

14. If an increase in the independent variable
causes a decrease in the dependent
variable, this is called a monotonic inverse
relationship. An inverse relationship is the
same thing as a negative correlation.
A monotonic direct relationship is where
an increase in the independent variable
causes an increase in the dependent
variable. In other words, there’s a positive
correlation between the data.

15. D = Difference of ranks
N = Number of Observations
Formula for the Spearman’s Rank Correlation Co-efficient
When the ranks are repeated the formula is
where m1, m2, ..., are the number of
repetitions of ranks

16. Example
English
(mark)
Maths
(mark)
Rank
(English)
Rank
(maths)
d d2
56 66 9 4 5 25
75 70 3 2 1 1
45 40 10 10 0 0
71 60 4 7 3 9
62 65 6 5 1 1
64 56 5 9 4 16
58 59 8 8 0 0
80 77 1 1 0 0
76 67 2 3 1 1
61 63 7 6 1 1

17. Artificial
Dichotomy
Continuous
One
Variable
Other
Variable
Biserial Correlation
Estimate of the relationship between a
continuous variable and a dichotomous variable.
The Term ‘Dichotomous’ means cut into two
parts or divided into two categories
rbis

18. Artificial Dichotomy
Socially adjusted Socially maladjusted
Athletic non-athletic
Radical Conservative
Poor Not poor
Social minded Mechanical minded
Drop outs Stay-ins
Successful Unsuccessful
Moral immoral
Natural Dichotomy
Right Wrong
Male Female
Living Dead
Owning a home Not owing a home
Being a farmer Not being a farmer
Being a Ph.D Not being a Ph.D
Living in Delhi Not living in Delhi

19. Formula for biserial correlation is
rbis biserial r
Mp & Mq Mean test scores
respectively for those who
pass and fail the item
p & q Proportions who pass and
fail the item
y height of the ordinate of the
normal curve at the point of
division between p and q
proportions of cases
 SD of the entire group

21. Point Biserial Correlation
Genuine or
Natural
Dichotomy
Continuous
One
Variable
Other
Variable
Estimating the relationship
between two variables when one
variables is in a continuous state
and other is in the state of a
natural or genuine dichotomy.
The Term ‘Dichotomous’ means cut
into two parts or divided into two
categories
rp, bis

22. Formula for point biserial
correlation is
Where
rpbis = Point biserial correlation
Mp = Mean of the 1st group
Mq = Mean of the 2nd group
P = Proportion of 1st group
Q = Proportion of 2nd group
 = Standard Deviation of the total group

24. Tetrachoric Correlation
Estimating the relationship between two
variables when both variables are
dichotomous.
Eg: To study the relationship between
intelligence and emotional maturity, the first
variable, ‘Intelligence’ may be dichotomised as
above average and below average and the
other variable ‘emotional maturity’, as
emotionally mature and emotionally immature.
Dichotomous
Dichotomous
Tetrachoric correlation is suitable for situations
in which neither of the two variables can be
measured in terms of scores but both the
variables can be separated in terms of two
categories.
Eg: if we want to study the relationship
between ‘adjustment’ and ‘success’ in a job, we
can dichotomize the variables as adjusted-
maladjusted and success-failure.
rt.

25. Pass Fail
Trained (A) (B)
Untrained (C) (D)
Formula for Tetrachoric Correlation is
If AD is greater than BC, then the correlation is Positive
If BC is greater than AD, then the correlation is negative.

27. Phi Coefficient
Compute correlation / relationship
between two variables which are
genuinely dichotomous
Phi coefficient correlation is suitable
for situations in which neither of the
two variables can be measured in
terms of scores but both the variables
can be separated in terms of two
categories. When both the variables
are dichotomous in the same
attributes, we can use the phi
coefficient correlation rt.
Genuine
Dichotomous
Same
attributes
Genuine
Dichotomous


28. Pass Fail
Pass (A) (B)
Fail (C) (D)
Fail Pass
Pass (B) (A)
Fail (D) (C)
Favourable unfavourable
Favourable (A) (B)
unfavourable (C) (D)
If AD is greater than BC, then the correlation is Positive
If BC is greater than AD, then the correlation is negative.
Formula for Phi Coefficient ()
correlation is

30. Types of Correlation Coefficients
Correlation Coefficient Types of Scales
Pearson product-moment Both Scales - Interval (or) Ratio
Spearman rank-order Both Scales - Ordinal
Phi Both scales are naturally dichotomous (nominal)
Tetrachoric Both scales are artificially dichotomous (nominal)
Point-biserial
One scale naturally dichotomous (nominal),
one scale interval (or ratio)
Biserial
One scale artificially dichotomous (nominal),
one scale interval (or ratio)
Gamma One scale nominal, one scale ordinal