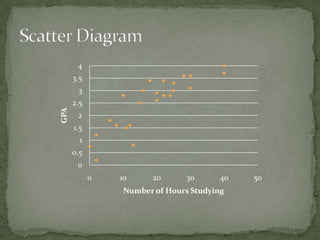
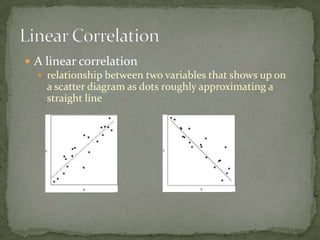
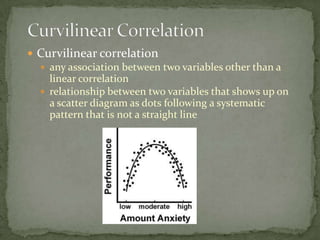
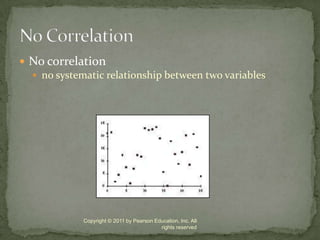
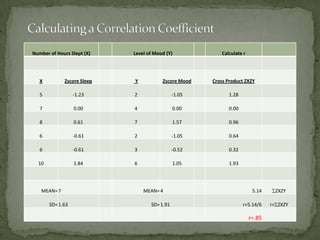
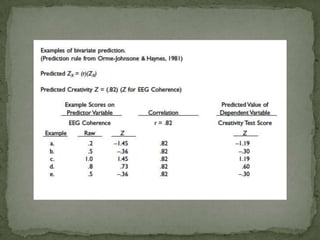
This document discusses correlation and prediction. It defines correlation as describing the relationship between two equal-interval numeric variables. A scatter diagram can be used to examine the pattern, direction, and strength of a correlation by plotting the values of one variable on the x-axis and the other on the y-axis. The correlation coefficient r quantifies the correlation and ranges from -1 to 1, with values farther from 0 indicating a stronger linear correlation. Prediction involves using the correlation between a predictor variable and a criterion variable to estimate values of the criterion variable based on values of the predictor variable.

1. Chapter 3Correlation and PredictionCopyright © 2011 by Pearson Education, Inc. All rights reservedAron, Coups, & Aron

2. Can be thought of as a descriptive statistic for the relationship between two variablesDescribes the relationship between two equal-interval numeric variablese.g., the correlation between amount of time studying and amount learned e.g., the correlation between number of years of education and salaryCopyright © 2011 by Pearson Education, Inc. All rights reservedCorrelations

3. Scatter Diagram

4. To make a scatter diagram:Draw the axes and decide which variable goes on which axis.The values of one variable go along the horizontal axis and the values of the other variable go along the vertical axis.Determine the range of values to use for each variable and mark them on the axes.Numbers should go from low to high on each axis starting from where the axes meet .Usually your low value on each axis is 0.Each axis should continue to the highest value your measure can possibly have.Make a dot for each pair of scores.Find the place on the horizontal axis for the first pair of scores on the horizontal-axis variable.Move up to the height for the score for the first pair of scores on the vertical-axis variable and mark a clear dot.Keep going until you have marked a dot for each person.Copyright © 2011 by Pearson Education, Inc. All rights reservedGraphing a Scatter Diagram

5. A linear correlationrelationship between two variables that shows up on a scatter diagram as dots roughly approximating a straight lineLinear Correlation

6. Curvilinear CorrelationCurvilinear correlationany association between two variables other than a linear correlationrelationship between two variables that shows up on a scatter diagram as dots following a systematic pattern that is not a straight line

7. No correlationno systematic relationship between two variablesCopyright © 2011 by Pearson Education, Inc. All rights reservedNo Correlation

8. Positive CorrelationHigh scores go with high scores.Low scores go with low scores.Medium scores go with medium scores.When graphed, the line goes up and to the right.e.g., level of education achieved and income Negative CorrelationHigh scores go with low scores. e.g., the relationship between fewer hours of sleep and higher levels of stressStrength of the Correlationhow close the dots on a scatter diagram fall to a simple straight lineCopyright © 2011 by Pearson Education, Inc. All rights reservedPositive and Negative Linear Correlation

9. Use a scatter diagram to examine the pattern, direction, and strength of a correlation.First, determine whether it is a linear or curvilinear relationship.If linear, look to see if it is a positive or negative correlation.Then look to see if the correlation is large, small, or moderate.Approximating the direction and strength of a correlation allows you to double check your calculations later.Copyright © 2011 by Pearson Education, Inc. All rights reservedImportance of Identifying the Pattern of Correlation

10. A number that gives the exact correlation between two variablescan tell you both direction and strength of relationship between two variables (X and Y)uses Z scores to compare scores on different variablesCopyright © 2011 by Pearson Education, Inc. All rights reservedThe Correlation Coefficient

11. The Correlation Coefficient ( r )The sign of r (Pearson correlation coefficient) tells the general trend of a relationship between two variables.+ sign means the correlation is positive.- sign means the correlation is negative.The value of r ranges from -1 to 1.A correlation of 1 or -1 means that the variables are perfectly correlated.0 = no correlation

12. Strength of Correlation CoefficientsThe value of a correlation defines the strength of the correlation regardless of the sign.e.g., -.99 is a stronger correlation than .75

13. r = ∑ZxZyNZx = Z score for each person on the X variableZy = Z score for each person on the Y variableZxZy = cross-product of Zx and Zy ∑ZxZy = sum of the cross-products of the Z scores over all participants in the studyCopyright © 2011 by Pearson Education, Inc. All rights reservedFormula for a Correlation Coefficient

14. Change all scores to Z scores.Figure the mean and the standard deviation of each variable.Change each raw score to a Z score.Calculate the cross-product of the Z scores for each person.Multiply each person’s Z score on one variable by his or her Z score on the other variable.Add up the cross-products of the Z scores.Divide by the number of people in the study.Copyright © 2011 by Pearson Education, Inc. All rights reservedSteps for Figuring the Correlation Coefficient

15. Calculating a Correlation Coefficient

16. Direction of causalitypath of causal effect (e.g., X causes Y)You cannot determine the direction of causality just because two variables are correlated.Copyright © 2011 by Pearson Education, Inc. All rights reservedIssues in Interpreting the Correlation Coefficient

17. Variable X causes variable Y.e.g., less sleep causes more stress Variable Y causes variable X.e.g., more stress causes people to sleep lessThere is a third variable that causes both variable X and variable Y.e.g., working longer hours causes both stress and fewer hours of sleepCopyright © 2011 by Pearson Education, Inc. All rights reservedReasons Why We cannot Assume Causality

18. Longitudinal Studya study where people are measured at two or more points in timee.g., evaluating number of hours of sleep at one time point and then evaluating their levels of stress at a later time pointTrue Experimenta study in which participants are randomly assigned to a particular level of a variable and then measured on another variablee.g., exposing individuals to varying amounts of sleep in a laboratory environment and then evaluating their stress levels Copyright © 2011 by Pearson Education, Inc. All rights reservedRuling Out Some Possible Directions of Causality

19. The Statistical Significance of a Correlation CoefficientA correlation is statistically significant if it is unlikely that you could have gotten a correlation as big as you did if in fact there was no relationship between variables. If the probability (p) is less than some small degree of probability (e.g., 5% or 1%), the correlation is considered statistically significant.

20. Predictor Variable (X)variable being predicted frome.g., level of education achievedCriterion Variable (Y)variable being predicted to e.g., incomeIf we expect level of education to predict income, the predictor variable would be level of education and the criterion variable would be income.Copyright © 2011 by Pearson Education, Inc. All rights reservedPrediction

21. Prediction ModelA person’s predicted Z score on the criterion variable is found by multiplying the standardized regression coefficient () by that person’s Z score on the predictor variable.Formula for the prediction model using Z scores:Predicted Zy = ()(Zx) Predicted Zy = predicted value of the particular person’s Z score on the criterion variable YZx = particular person’s Z score in the predictor variable XCopyright © 2011 by Pearson Education, Inc. All rights reservedPrediction Using Z Scores

22. Determine the standardized regression coefficient ().Multiply the standardized regression coefficient () by the person’s Z score on the predictor variable.Copyright © 2011 by Pearson Education, Inc. All rights reservedSteps for Prediction Using Z Scores

24. So, let’s say that we want to try to predict a person’s oral presentation score based on a known relationship between self-confidence and presentation ability. Which is the predictor variable (Zx)? The criterion variable (Zy)?If r = .90 and Zx = 2.25 then Zy = ?So what? What does this predicted value tell us?Copyright © 2011 by Pearson Education, Inc. All rights reservedHow Are You Doing?

25. Change the person’s raw score on the predictor variable to a Z score.Multiply the standardized regression coefficient () by the person’s Z score on the predictor variable.Multiply  by Zx.This gives the predicted Z score on the criterion variable.Predicted Zy = ()(Zx)Change the person’s predicted Z score on the criterion variable back to a raw score.Predicted Y = (SDy)(Predicted Zy) + MyCopyright © 2011 by Pearson Education, Inc. All rights reservedPrediction Using Raw Scores

26. Example of Prediction Using Raw Scores: Change Raw Scores to Z ScoresFrom the sleep and mood study example, we known the mean for sleep is 7 and the standard deviation is 1.63, and that the mean for happy mood is 4 and the standard deviation is 1.92. The correlation between sleep and mood is .85.Change the person’s raw score on the predictor variable to a Z score.Zx = (X - Mx) / SDx(4-7) / 1.63 = -3 / 1.63 = -1.84Copyright © 2011 by Pearson Education, Inc. All rights reserved

27. Example of Prediction Using Raw Scores: Find the Predicted Z Score on the Criterion VariableMultiply the standardized regression coefficient () by the person’s Z score on the predictor variable.Multiply  by Zx.This gives the predicted Z score on the criterion variable.Predicted Zy = ()(Zx) = (.85)(-1.84) = -1.56Copyright © 2011 by Pearson Education, Inc. All rights reserved

28. Example of Prediction Using Raw Scores: Change Raw Scores to Z ScoresChange the person’s predicted Z score on the criterion variable to a raw score.Predicted Y = (SDy)(Predicted Zy) + MyPredicted Y = (1.92)(-1.56) + 4 = -3.00 + 4 = 1.00Copyright © 2011 by Pearson Education, Inc. All rights reserved

29. Proportion of variance accounted for (r2)To compare correlations with each other, you have to square each correlation.This number represents the proportion of the total variance in one variable that can be explained by the other variable.If you have an r= .2, your r2= .04Where, a r= .4, you have an r2= .16 So, relationship with r = .4 is 4x stronger than r=.2The Correlation Coefficient and the Proportion of Variance Accounted for