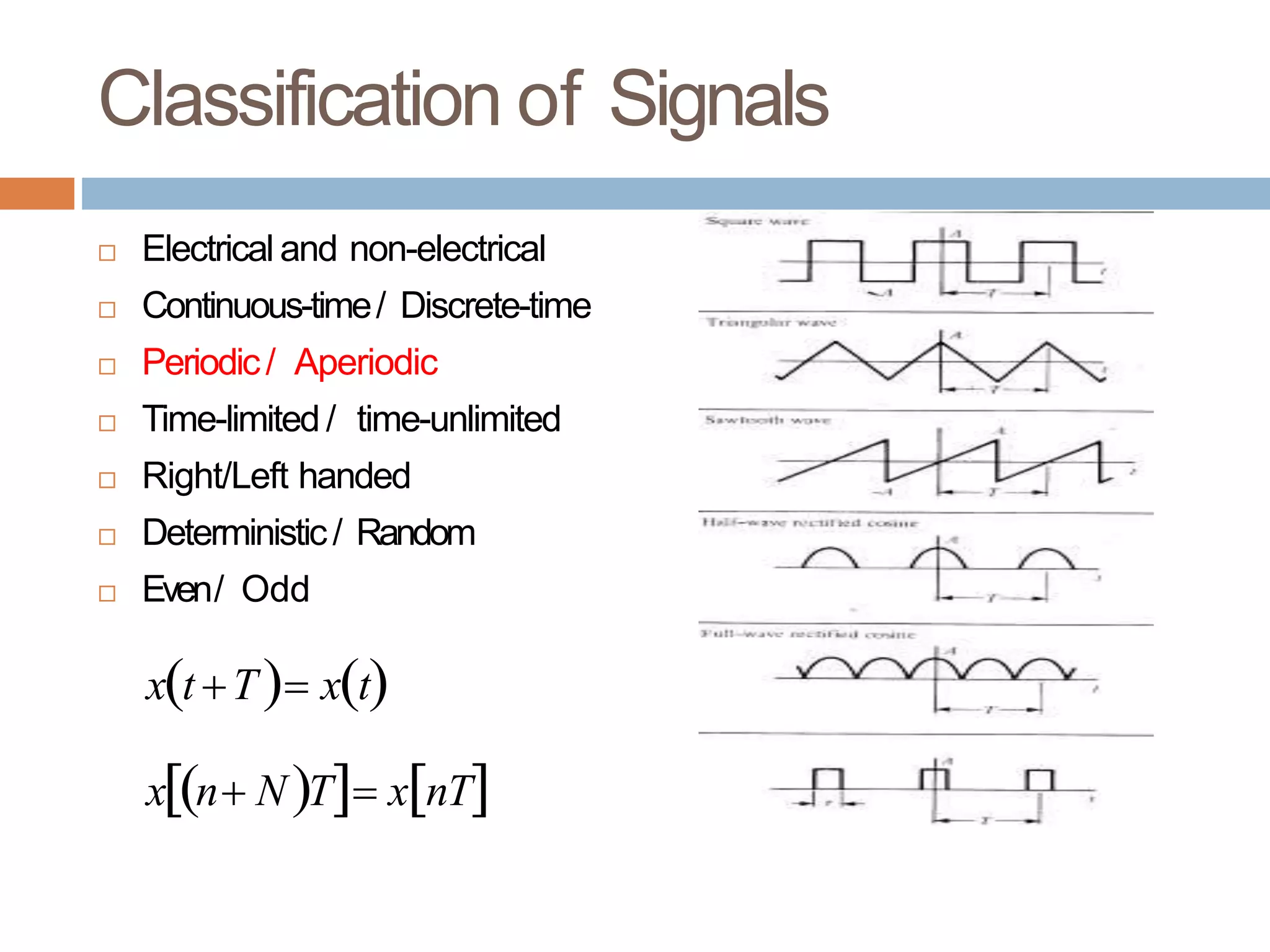
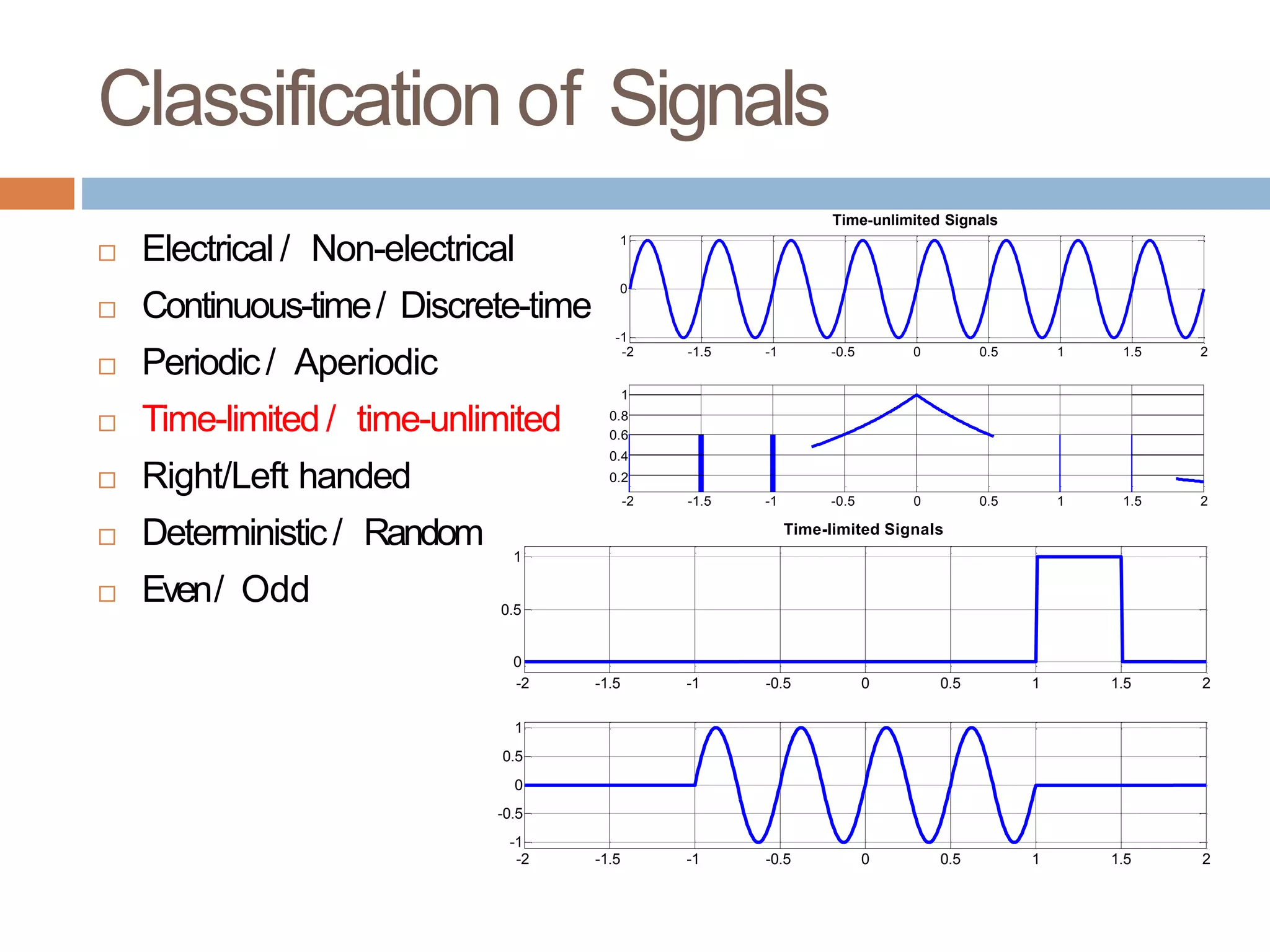
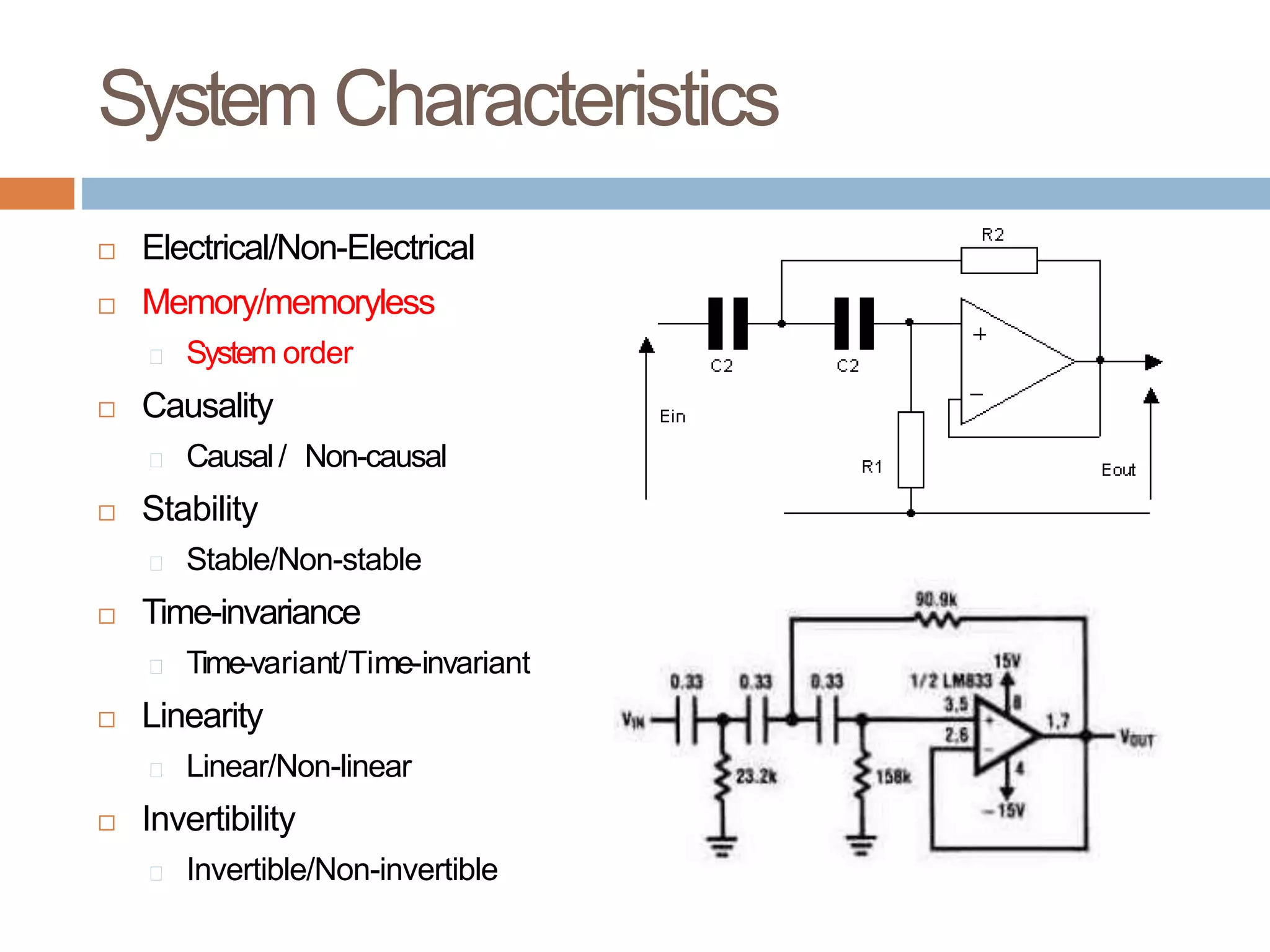
The document presents an introduction to signals and systems, outlining key topics, reading materials, and structure of the course. It covers definitions of signals, classifications of signals based on various criteria, and basic operations like time-shifting, scaling, and reversal. Furthermore, it emphasizes the importance of understanding signal representation and mathematical manipulation in the context of linear time-invariant systems.

1. INTRODUCTIONTO
SIGNALSANDSYSTEMS
Lecture1

2. Thereading material
 Thetext book
Signalsand Systems
 Alan V
. Oppenheim
 Alan S. Willsky
 S. HamidNawab
 2nd Edition
 Web based demos

3. Thereading material
 Anauxiliarybook
Signalsand Linear
SystemsAnalysiswith
Matlab
 Gordon E.Carlson
 Second Ed.

4. T
ests
 Two tests
5 marks each
Thebest score
Nonobjective type
 No MCQ, No Blanks,No True/false
Subjectivetype tests only
 Definitions,Descriptions,Mathematical Evidences
 Arguments,Comparisons,Interpretations,Calculations,
and Conclusions etc.

5. Chapter 1
S.
No.
Topic
No. of
Lectures
1 Basic concepts of Signals and Systems 1
2 Signal representationand models 1
3
Classification of signals and Basic operations on
signals
1
4
System characteristics,linear time-invariant (LTI)
systems
1
5
System response, system equations and impulse
response, system order,Causality and Stability
1
Total 5

6. Definitions
 Signal
 Signal Processing
 System
 Carrier of information
Signal transmitted
from antenna
a radio
 Manipulating, Modifying,
transforming
Amplification/attenuation, Rectification,
Modulation, Filtering, Mixing
 A setup / set of components that
processesthesignals
Man
Robot

7. Classification of Signals
 Electrical and non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd

8. Classification of Signals
 Electrical and non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
-1
.5
0
.5
1
xt
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
1
.5
0
.5
-1
xnT

9. Classification of Signals
 Electrical and non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd

10. Classification of Signals
 Electrical and non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd
xt T xt
xn NT xnT

11. Classification of Signals
 Electrical / Non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
0
0.5
1
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
1
0.5
0
-0.5
-1
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
-1
0
1
Time-unlimited Signals
-2 -1.5 -1 -0.5 0
Time-limited Signals
0.5 1 1.5 2
1
0.8
0.6
0.4
0.2

12. Classification of Signals
 Electrical / Non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd

13. Classification of Signals
 Electrical / Non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
1
0
-1
Time-unlimited Signals
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
1
0.8
0.6
0.4
0.2

14. Classification of Signals
 Electrical / Non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Right/Left handed
 Deterministic/ Random
 Even/ Odd

15. Classification of Signals
 Electrical / Non-electrical
 Continuous-time/ Discrete-time
 Periodic/ Aperiodic
 Time-limited / time-unlimited
 Deterministic/ Random
 Right/Left handed
 Even/ Odd

16. Classification of Signals
 Electrical and non-electrical
 Periodic/ Aperiodic
 Continuous-time/ Discrete-time
 Time-limited / time-unlimited
 Deterministic/ Random
 Right/Left handed
 Even/ Odd
 Even Signal
x t  xt
xn xn
 Odd Signal
xt xt
xnxn

17. Classification of Signals
 Electrical and non-electrical
 Periodic/ Aperiodic
 Continuous-time/ Discrete-time
 Time-limited / time-unlimited
 Deterministic/ Random
 Right/Left handed
 Even/ Odd
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
-1
0
1
Time-unlimited Signals
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
1
0
-1

18. Evenor Odd ?
Even
Odd
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
0
1
2
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
-1
0
1
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
0
1
2
Neither Even
Nor Odd

19. Signal Representation
 Simple definition
Continuousthroughout
the domain from -∞ to ∞
 Piecewise definition
Continuousin the
subdomainsand
discontinuities at the
junctions
t
f t e


f t  
0
et
t  0
t  0
for all t

20. BasicTime-Operations onSignals
 Time-Shifting
Time advance
Time delay
 Time-Scaling
Compression
Expansion
 Time-Reversal
yt xat
a 1
a 1
yt xt
yt xt  
  0
  0
a 0

21. Time Shifting
 Time-Shifting
Time advance
Time delay
-2 -1.5 -1 -0.5 0.5 1 1.5 2
0
time
1
0.5
0
x(t+tau)
-2 -1.5 -1 -0.5 0.5 1 1.5 2
1
0.5
0
0
time
x(t)
yt xt  
  0
  0
Time Shifting

22. Time Shifting
 Time-Shifting
Time advance
Time delay
yt xt  
  0
  0
Time Shifting
-2 -1.5 -1 -0.5 0.5 1 1.5 2
1
0.5
0
0
time
x(t+tau)
-2 -1.5 -1 -0.5 0.5 1 1.5 2
0
time
1
0.5
0
x(t)

23. Time Scaling
 Time-Scaling
Compression
Expansion
a 0
-3 -2 -1 0 1 2 3
1
0.5
0
yt xat
a 1
a 1
Time Scaling
x(2t)
-3 -2 -1 0 1 2 3
1
0.5
0
x(0.5t)
-3 -2 -1 0 1 2 3
1
0.5
0
x(t)

24. Time Reversal
 Time-Reversal
-3 -2 -1 1 2 3
0
time
yt xt
Time Reversal
1
0.5
0
x(-t)
-3 -2 -1 1 2 3
1
0.5
0
0
time
x(t)

25. Evenor Odd ?
Even
Odd
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
0
1
2
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
-1
0
1
-2 -1.5 -1 -0.5 0 0
.5 1 1
.5 2
0
1
2
Neither Even
Nor Odd

26. x(t) = xe(t) + xo(t)
Even Signal Odd Signal
xt xe t xo t
xt xe t xo t
xt xe t xo t
xt xt 2xe t
x t
1
xt xt
e
2
xt xt 2xo t
x t
1
xt xt
o
2
+

27. x(t) = xe(t) + xo(t)
Even Signal Odd Signal
xt xe t xo t
xt xe t xo t
xt xe t xo t
xt xt 2xe t
e
2
x t
1
xt xt
xt xt 2xo t
x t
1
xt xt
o
2
+

28. x(t) = xe(t) + xo(t)
Even Signal Odd Signal
xt xe t xo t
xt xe t xo t
xt xe t xo t
xt xt 2xe t
e
2
x t
1
xt xt
xt xt 2xo t
x t
1
xt xt
o
2
+ -

29. x(t) = xe(t) + xo(t)
Even Signal Odd Signal
xt xe t xo t
xt xe t xo t
xt xe t xo t
xt xt 2xe t
e
2
x t
1
xt xt
xt xt 2xo t
o
2
x t
1
xt xt
+ -

30. x(t) = xe(t) + xo(t)
Even Signal Odd Signal
xe t
xt xt
2
xt xt
2

o
x t
2
2
o
x t
e
x t 
 t xt xt
xt x
 
2
2
2
xt xt
xt xt
o
x t
e
x t   

2
xt
2

xt
  xt
o
x t
e
x t
2

31. Break into Evenand Odd parts
-2 -1.5 -1 -0.5 0.5 1 1.5 2
2
1.5
1
0.5
0
0
time (seconds)
x(t)

32. Break into Evenand Odd parts
-2 -1.5 -1 -0.5 0.5 1 1.5 2
2
1.5
1
0.5
0
0
time (seconds)
x(t)




xt 
2(t 1) 1 t  0
2 0  t 1
0 elsewhere
xt ?

33. Break into Evenand Odd parts
Graphically Mathematically
 



x t  
1 t  0
0  t  1
elsewhere
2
0
 2(t 1)




xt 
2(1t) 0  t 1
2 1 t  0
0 elsewhere
-2 -1.5 -1 -0.5 0.5 1 1.5 2
0
0.5
1
1.5
2
0
time (seconds)
x(-t)

34. Break into Evenand Odd parts
Graphically
-2 -1 0 1 2
0
1.5
1
0.5
2
x(t)
-2 -1 0 1 2
0
1.5
1
0.5
2
x(-t)
-2 -1 0 1 2
0
2
1.5
1
0.5
Even Part
-2 -1 0 1 2
-1
1
0.5
0
-0.5
Odd Part

35. Break into Evenand Odd parts
Mathematically




xt 
2(t 1) 1 t  0
2 0  t 1
0 elsewhere 



xt 
2(1t) 0  t 1
2 1 t  0
0 elsewhere



xt xt 
21 t
0 0
2(t 1) 2 1 t  0
0  t  1
elsewhere



xt xt 
1 t  0
3t 0  t 1
0 elsewhere
 2(t 2)



xt xt 
21 t
0 0
2(t 1) 2 1 t  0
0  t  1
elsewhere

36. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

37. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

38. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

39. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

40. System Characteristics
2
yt 2xt xt 1
1
xt  2
2
2
yn 2xn xn1
1
xn 2
2
yn 2xn xn1
1
xn 2
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant yt 2xt xt 1
1
xt  2
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

41. System Characteristics
 BIBO stability
Boundedoutputfor
bounded input
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Unstable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

42. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

43. System Characteristics
  
x t  y t
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/ Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible
xt   yt  

44. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible
1 1
x  y
x2  y2
Ax1  Bx2  Ay1  By2

45. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible
-2 -1.5 -1 -0.5 0.5 1 1.5 2
-2
-1
0
1
2
0
x(t)
y(t)
-2 -1.5 -1 -0.5 0.5 1 1.5 2
-4
-2
0
2
4
0
x(t)
y(t)
- 2 - 1 . 5 - 1 - 0 . 5 0 . 5 1 1 . 5 2
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
0
x(t )
y(t
)

46. System Characteristics
 Electrical/Non-Electrical
 Memory/memoryless
System order
 Causality
Causal/Non-causal
 Stability
Stable/Non-stable
 Time-invariance
Time-variant/Time-invariant
 Linearity
Linear/Non-linear
 Invertibility
Invertible/Non-invertible

47. System Representation
Block Diagram System Component

48. System Representation
Block Diagram System Component