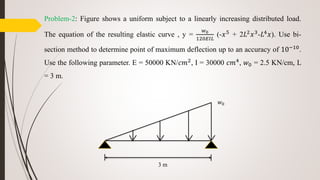
Numerical Methods and Analysis discusses various root-finding methods including bisection, false position, and Newton-Raphson. Bisection uses interval halving to find a root between two values with opposite signs. False position uses the slope of a line between two points to estimate the next root. Newton-Raphson approximates the root using Taylor series expansion neglecting higher order terms. Interpolation uses forward difference tables to construct a polynomial approximation of a function.

1. Numerical Methods and Analysis
Faruque Abdullah
Lecturer
Dept. of Civil Engineering
Dhaka International University

2. Roots of a equation
Roots of a equation is calculated by the following methods:
 Bi-section method
 Iteration method
 Method of false position/ Interpolation method
 Newton Raphson method, etc.

3. Bi-section/ Interval Halving Method(IVT)
IVT: If a function f(x) is continuous between a and b and f(a) and
f(b) is opposite sign, then there exists at least one root between a
and b.
f(x) = 𝑥4
- 2x;
f(2) = -ve
f(3) = +ve
 x =
𝑎+𝑏
2
=
2+3
2
= 2.5

4. Procedure:
Step-1: Choose a real two numbers a and b such that f(a)f(b)<0
Step-2: Set, 𝑥 𝑟 =
𝑎+ 𝑏
2
Step-3: a) If f(a) f(𝑥 𝑟) < 0, the root lies in the interval (a,𝑥 𝑟), Then
set b = 𝑥 𝑟 and go to step 2.
b) If f(a) f(𝑥 𝑟) > 0, the root lies in the interval (𝑥 𝑟,b), Then
set a = 𝑥 𝑟 and go to step 2.
c) If f(a) f(𝑥 𝑟) = 0, it means that 𝑥 𝑟 is a root of the
equation f(x) = 0 and the computation may be terminated.

5. Problem-1: Find a real root of the equation 𝑥3- 2x-5 = 0 by bi-section method
up to an accuracy of 10−4.
Solution: Let, f(x) = 𝑥3 - 2x -5
f(2) = 23 - 2.2 – 5 = -1
f(3) = 33
- 2.3 – 5 = 16
As f(2) is –ve and f(3) is +ve .
So f(2) f(3) < 0.
 Root lies between 2 and 3.

6. n a b 𝑥 𝑟 f(x)
(sign)
f(x)
1 2 3 2.5 +ve +5.63
2 2 2.5 2.25 +ve +1.89
3 2 2.25 2.125 +ve +0.34
4 2 2.125 2.0625 -ve -0.35
5 2.0625 2.125 2.09375 -ve -8.94 x10−3
6 2.09375 2.125 2.109375 +ve +0.17
7 2.09375 2.109375 2.1015625 +ve +0.08
8 2.09375 2.1015625 2.09765625 +ve +0.03
9 2.09375 2.09765625 2.095703125 +ve +0.01
10 2.09375 2.095703125 2.094726563 +ve +1.95 x 10−3
11 2.09375 2.094726563 2.094238282 -ve -3.5 x 10−3
12 2.094238282 2.094726563 2.094482423 -ve -7.7 x 10−4

7. Problem-2: Figure shows a uniform subject to a linearly increasing distributed load.
The equation of the resulting elastic curve , y =
𝑤0
120𝐸𝐼𝐿
(-𝑥5
+ 2𝐿2
𝑥3
-𝐿4
𝑥). Use bi-
section method to determine point of maximum deflection up to an accuracy of 10−10
.
Use the following parameter. E = 50000 KN/𝑐𝑚2, I = 30000 𝑐𝑚4, 𝑤0 = 2.5 KN/cm, L
= 3 m.
3 m
𝑤0

8. Solution: For maximum deflection,
𝑑𝑦
𝑑𝑥
= 0

𝑑𝑦
𝑑𝑥
=
𝑤0
120𝐸𝐼𝐿
x
𝑑𝑦
𝑑𝑥
(-𝑥5 + 2 𝐿2 𝑥3-𝐿4 𝑥)
=
𝑤0
120𝐸𝐼𝐿
x (-5𝑥4 + 6 𝐿2 𝑥2-𝐿4)
=
2.5
120 X 50000 X 30000 X 300
x (-5𝑥4 + 6. 3002 𝑥2-3004)
= 4.63 x 10−14 x (- 5𝑥4 + 540000 𝑥2- 3004)

9. Let, f(x) = 4.63 x 10−14
x (- 5𝑥4
+ 540000 𝑥2
- 3004
)
f(134) = -7.34 x 10−7
f(135) = 3.73 x 10−6
As f(134) is –ve and f(135) is +ve .
So f(134) f(135) < 0.
 Root lies between 134 and 135.

10. n a b 𝑥 𝑟 f(x)
(sign)
f(x)
1 134 135 134.5 +ve +1.5 x 10−6
2 134 134.5 134.25 +ve +3.84 10−7
3 134 134.25 134.125 -ve -1.75 x 10−7
4 134.125 134.25 134.1875 +ve +1.05 x 10−7
5 134.125 134.1875 134.15625 -ve -3.5 x 10−8
6 134.15625 134.1875 134.171875 +ve +3.5 x 10−8
7 134.15625 134.171875 134.1640625 -ve -7.22 x 10−11

11. Method of False Position
(0,0)
X
Y
[a, f(a)]
[b, f(b)]
f(x) 𝑦−𝑓(𝑎)
𝑥−𝑎
=
𝑓 𝑏 − 𝑓(𝑎)
𝑏−𝑎
Let, y = 0,
−𝑓(𝑎)
𝑥−𝑎
=
𝑓 𝑏 − 𝑓(𝑎)
𝑏−𝑎
 x-a = -
(𝑏−𝑎)𝑓(𝑎)
𝑓 𝑏 −𝑓(𝑎)
 x = a -
(𝑏−𝑎)𝑓(𝑎)
𝑓 𝑏 −𝑓(𝑎)
Derive the root of a curve f(x) by False Position method.

12. Newton Raphson Method
Let, 𝑥0 be a root of the function f(𝑥0) = 0 and assume that 𝑥1 = 𝑥0 + h be the correct
root of the function f(𝑥1) = 0.
𝑥1 = 𝑥0 + h -----------------(1)
f(𝑥1) = 0
f(𝑥0 + h) = 0-----------------(2)
Expanding eq (2) by Tailor’s series we get,
f(𝑥0) + h𝑓′(𝑥0) +
ℎ2
2!
𝑓′′(𝑥0) + ----- = 0

13. Neglecting 2nd and higher order derivatives,
f(𝑥0) + h𝑓′
(𝑥0) = 0
Or, h = -
f( 𝑥0)
𝑓′( 𝑥0)
From eq (1),
𝑥1 = 𝑥0 -
f( 𝑥0)
𝑓′( 𝑥0)
Similar approximation for 𝑥2, 𝑥3, ----, 𝑥 𝑛+1 we get,
𝑥2 = 𝑥1 -
f( 𝑥1)
𝑓′( 𝑥1)

14. 𝑥3 = 𝑥2 -
f( 𝑥2)
𝑓′( 𝑥2)
-------------
𝑥 𝑛+1 = 𝑥 𝑛 -
f( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
This is Newton Raphson Formula.

15. Problem-3: Find a real root of the equation 𝑥3- 2x-5 = 0 by Newton Raphson
method.
Solution: Let, f(x) = 𝑥3 - 2x -5
f(𝑥 𝑛) = 𝑥 𝑛
3 - 2𝑥 𝑛 -5
𝑓′(𝑥 𝑛) = 3𝑥 𝑛
2
- 2
From Newton Raphson Formula,
𝑥 𝑛+1 = 𝑥 𝑛 -
f( 𝑥 𝑛)
𝑓′( 𝑥 𝑛)
= 𝑥 𝑛 -
𝑥 𝑛
3 − 2 𝑥 𝑛 −5
3𝑥 𝑛
2 − 2

16. Putting n=0,
𝑥1 = 𝑥0 -
𝑥0
3 − 2 𝑥0 −5
3𝑥0
2 − 2
Assume, 𝑥0 = 2
𝑥1 = 2 -
23 − 2(2) −5
3(22) − 2
= 2.1
𝑥2 = 2.1 -
2.13 − 2(2.1) −5
3(2.1)2 − 2
= 2.0946
𝑥3 = 2.0946 -
2.09463 − 2(2.0946) −5
3(2.0946)2 − 2
= 2.0946

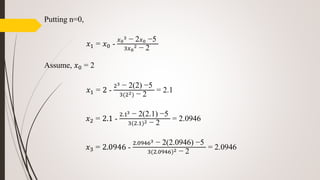
17. Problem-4: You are designing a spherical tank to hold water for a small village in a
developing country. The volume of liquid can be calculated as V = πℎ2 [3𝑅−ℎ]
3
. If R = 3
m, to what depth must the tank be filled so that it holds 30 𝑚3 water?
Solution: V = πℎ2 [3𝑅−ℎ]
3
=> 30 = πℎ2 [3.3−ℎ]
3
=> 90 = πℎ2(9-h)
=>
90
𝜋
= 9ℎ2 - ℎ3
=> ℎ3
- 9ℎ2
+ 28.65 = 0

18. Let, f(h) = ℎ3 - 9ℎ2 + 28.65
f(ℎ 𝑛) = ℎ 𝑛
3
- 9ℎ 𝑛
2
+ 28.65
𝑓′(ℎ 𝑛) = 3ℎ 𝑛
2
- 18ℎ 𝑛
From Newton Raphson Formula,
ℎ 𝑛+1 = ℎ 𝑛 -
f(ℎ 𝑛)
𝑓′(ℎ 𝑛)
= ℎ 𝑛 -
ℎ 𝑛
3
− 9ℎ 𝑛
2
+ 28.65
3ℎ 𝑛
2
−18ℎ 𝑛

19. Putting n=0,
ℎ1 = ℎ0 -
ℎ0
3
− 9ℎ0
2
+ 28.65
3ℎ0
2
− 18ℎ0
Assume, ℎ0 = 2
ℎ1 = 2 -
23 − 9(2)2+28.65
3(22) −18(2)
= 2.027
ℎ2 = 2.027 -
2.0273 − 9(2.027)2+28.65
3(2.0272) −18(2.027)
= 2.02699
ℎ3 = 2.02699 -
2.026993 − 9(2.02699)2+28.65
3(2.026992) −18(2.02699)
= 2.02699
Required depth is 2.02699 m to hold 30 𝑚3 volume of water in the tank.

20. Interpolation

21. Interpolation Method
Forward difference table:
x y ∆ ∆2 ∆3 ∆4
∆5 ∆6
x0 y0
∆y0
x1 y1 ∆2y0
∆y1 ∆3y0
x2 y2 ∆2
y1 ∆4
y0
∆y2 ∆3
y1 ∆5
y0
x3 y3 ∆2
y2 ∆4
y1 ∆6
y0
∆y3 ∆3y2 ∆5y1
x4 y4 ∆2
y3 ∆4
y2
∆y4 ∆3y3
x5 y5 ∆2
y4
∆y5
x6 y6

22. ∆y0 = y1 - y0
∆2
y0 = ∆y1 - ∆y0 = y2 - y1- y1 + y0 = y2 - 2y1 + y0
∆3
y0 = ∆2
y1 - ∆2
y0 = y3 - 2 y2 + y1 - y2 + 2 y1 - y0 = y3 - 3 y2 + 3 y1 - y0
--------------------------------------------Continue--------------------------------------------

23. Newton’s Formula for Forward Interpolation
Let, y = f(x) denote a function which takes the values from y0, y1, y2,
y3,……….., yn for the equidistance values x0, 𝑥1, 𝑥2, 𝑥3,……….., xn. Φ(x)
denote a function of polygonal for nth degree. As x is equidistance xi = x0 +
ih. Where, i = 1,2,3,…….,n.
x1 = x0 + h
=> (x1 - x0) = h
x2 = x0 + 2h
=> (x2 - x0) = 2h

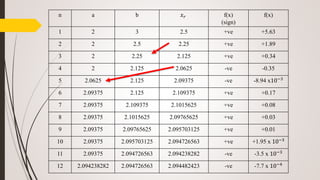
24. The polynomial φ(x) = 𝑎0 + 𝑎1 (x-x0) + 𝑎2 (x-x0) (x-x1) + 𝑎3 (x-x0) (x-x1) (x-x2)
+ ………………..+ 𝑎 𝑛 (x-x0) (x-x1) (x-x2)………… (x-x 𝑛−1) ………(1)
When, x = 𝑥0, φ(x) = 𝑎0 = 𝑦0
When, x = 𝑥1, φ(x) = 𝑎0 + 𝑎1 (x1 -x0) = 𝑦1
 𝑎1 =
𝑦1−𝑦0
𝑥1−𝑥0
=
∆y0
ℎ
When, x = 𝑥2, φ(x) = 𝑎0 + 𝑎1 (x2 -x0) + 𝑎2 (x2 -x0) (x2 -x1) = 𝑦2
=> 𝑦2 = 𝑦0 +
∆y0
ℎ
. 2h + 𝑎2 . 2h . h [∆y0 = 𝑦1-𝑦0]
=> 𝑎2 =
𝑦2−2𝑦1+ 𝑦0
2ℎ2 =
∆2y0
2!ℎ2

25. Similarly we can write,
𝑎3 =
∆3y0
3!ℎ3 ; 𝑎4 =
∆4y0
4!ℎ4 ; ……., 𝑎 𝑛 =
∆ny0
𝑛!ℎ 𝑛
Putting this value in eq (1), we get,
φ(x) = 𝑦0 +
∆y0
ℎ
(x-x0) +
∆2y0
2!ℎ2 (x-x0) (x-x1) +
∆3y0
3!ℎ3 (x-x0) (x-x1) (x-x2) +
………………..+
∆ny0
𝑛!ℎ 𝑛(x-x0) (x-x1) (x-x2)………… (x-x 𝑛−1)
Let us assume, x = x0 + ph
=> p =
𝑥 − 𝑥0
ℎ

26. =>
𝑥 − 𝑥1
ℎ
=
𝑥 −𝑥0−ℎ
ℎ
=
𝑥 −𝑥0
ℎ
- 1= p-1
=>
𝑥 − 𝑥2
ℎ
=
𝑥 −𝑥0−2ℎ
ℎ
=
𝑥 −𝑥0
ℎ
- 2 = p-2
φ(x) = 𝑦0 +
∆y0
ℎ
(x-x0) +
∆2y0
2!ℎ2 (x-x0) (x-x1) +
∆3y0
3!ℎ3 (x-x0) (x-x1) (x-x2) +
………………..+
∆ny0
𝑛!ℎ 𝑛(x-x0) (x-x1) (x-x2)………… (x-x 𝑛−1)
 φ(x) = 𝑦0 + p ∆y0 + p (p-1)
∆2y0
2!
+ p (p-1)(p-2)
∆3y0
3!
+ ………………..+ p (p-1)
(p-2) ……… p(p-n+1)
∆ny0
𝑛!

27. Problem-5: Find the cubic polynomial which takes the following values
y(1) = 24
y(3) = 120
y(5) = 336
y(7) = 720
Hence, obtain the values of y(8) by Newton’s Forward Interpolation method.

28. Solution: We make the forward difference table,
h = (x1 - x0) = 3 – 1 = 2
x = 𝑥0 + ph => p =
𝑥 − 𝑥0
ℎ
=> p =
8 −1
2
= 3.5
x y ∆ ∆2 ∆3
1 24
96
3 120 120
216 48
5 336 168
384
7 720

29. From Newton’s formula for forward interpolation,
y(x) = 𝑦0 + p∆ 𝑦0 + p (p-1)
∆2 𝑦0
2!
+ p (p-1) (p-2)
∆3 𝑦0
3!
=> y(8)= 24 + 3.5 x 96 + 3.5 (3.5-1) x
120
2!
+ 3.5 (3.5-1) (3.5-2) x
48
3!
= 990.

30. Problem-6: Find the cubic polynomial which takes the following values
y(1) = 24
y(3) = 120
y(5) = 336
y(7) = 720
Hence, obtain the values of y(6) by Newton’s Backward Interpolation method.
Newton’s Formula for Backward Interpolation

31. Solution: We make the backward difference table,
h = (x1 - x0) = 3 – 1 = 2
x = 𝑥 𝑛 + ph => p =
𝑥 − 𝑥 𝑛
ℎ
=> p =
6 −7
2
= -0.5
x y ∇ ∇ 2
∇ 3
1 24
96
3 120 120
216 48
5 336 168
384
7 720

32. From Newton’s formula for backward interpolation,
y(x) = 𝑦𝑛 + p∆ 𝑦𝑛 + p (p+1)
∆2 𝑦 𝑛
2!
+ p (p+1)(p+2)
∆3 𝑦 𝑛
3!
=> y(6)= 720 + (-0.5) x 384 + (-0.5) (-0.5+1) x
168
2!
+ (-0.5) (-0.5+1) (-0.5+2) x
48
3!
= 576.

33. Problem-6: The table shows the value of tanx for 0.1 ≤ x ≤ 0.3
Find, (a) tan(0.12) by Forward Interpolation Method
(b) tan(0.26) by Backward Interpolation Method.
x Y = tanx
0.10 0.1745
0.15 0.2618
0.20 0.3491
0.25 0.4363
0.30 0.5236

34. Solution: We make the forward difference table,
x y ∆ ∆2
∆3
∆4
0.10 0.1745
0.0873
0.15 0.2618 0
0.0873 0
0.20 0.3491 0 0
0.0873 0
0.25 0.4364 0
0.0873
0.30 0.5237

35. (a) h = (x1 - x0) = 0.15 – 0.10 = 0.05
x = 𝑥0 + ph => p =
𝑥 − 𝑥0
ℎ
=> p =
0.12 −0.10
0.05
= 0.4
For Newton’s Forward formula,
tan(0.12) = 𝑦0 + p∆ 𝑦0 + p (p-1)
∆2 𝑦0
2!
+ p (p-1) (p-2)
∆3 𝑦0
3!
+ p (p-1) (p-2) (p-3)
∆4 𝑦0
4!
= 0.1745 + 0.4 x 0.0873 + 0.4 (0.4-1)
0
2!
+ 0.4 (0.4-1) (0.4-2)
0
3!
+
0.4 (0.4-1) (0.4-2)
0
4!
= 0.2094

36. (b) h = (x1 - x0) = 0.15 – 0.10 = 0.05
x = 𝑥 𝑛 + ph => p =
𝑥 − 𝑥 𝑛
ℎ
=> p =
0.26 −0.30
0.05
= -0.8
For Newton’s Backward formula,
tan(0.26) = 𝑦𝑛 + p∆ 𝑦𝑛 + p (p+1)
∆2 𝑦 𝑛
2!
+ p (p+1) (p+2)
∆3 𝑦 𝑛
3!
+ p (p+1) (p+2) (p+3)
∆4 𝑦 𝑛
4!
= 0.5237 + -0.8 x 0.0873 + -0.8 (-0.8+1)
0
2!
- 0.8 (-0.8+1) (-0.8+2)
0
3!
-
0.8 (-0.8+1) (-0.8+2)
0
4!
= 0.4538

37. Problem-7: The discharge through a hydraulic structure for different values of
head (H) is shown in table.
Calculate discharge, Q for H=3 ft using Lagrange formula.
H (ft) 1.2 2.1 2.7 4.0
Q (cusec) 25 60 90 155

38. Solution: From Lagrange formula,
Q (cusec) =
(𝑥−𝑥1)(𝑥−𝑥2)(𝑥−𝑥3)
(𝑥0−𝑥1)(𝑥0−𝑥2)(𝑥0−𝑥3)
𝑦0 +
(𝑥−𝑥0)(𝑥−𝑥2)(𝑥−𝑥3)
(𝑥1−𝑥0)(𝑥1−𝑥2)(𝑥1−𝑥3)
𝑦1 +
(𝑥−𝑥0)(𝑥−𝑥1)(𝑥−𝑥3)
(𝑥2−𝑥0)(𝑥2−𝑥1)(𝑥2−𝑥3)
𝑦2 +
(𝑥−𝑥0)(𝑥−𝑥1)(𝑥−𝑥2)
(𝑥3−𝑥0)(𝑥3−𝑥1)(𝑥3−𝑥2)
𝑦3
=
(3−2.1)(3−2.7)(3−4)
(1.2−2.1)(1.2−2.7)(1.2−4)
25 +
(3−1.2)(3−2.7)(3−4)
(2.1−1.2)(2.1−2.7)(2.1−4)
60 +
(3−1.2)(3−2.1)(3−4)
2.7−1.2 2.7−2.1 (2.7−4)
90 +
(3−1.2)(3−2.1)(3−2.7)
(4−1.2)(4−2.1)(4−2.7)
155
= 1.78 – 31.58 + 124.62 + 10.89 = 105.71 cusec.

39. Exercise: The load bearing capacity on different penetration level is given
below.
Calculate Load for D = 3.00 cm using Lagrange formula.
D (cm) 2.35 2.75 3.30 3.60
Load (KN) 25 43 66 70

40. Solution: From Lagrange formula,
Q (cusec) =
(𝑥−𝑥1)(𝑥−𝑥2)(𝑥−𝑥3)
(𝑥0−𝑥1)(𝑥0−𝑥2)(𝑥0−𝑥3)
𝑦0 +
(𝑥−𝑥0)(𝑥−𝑥2)(𝑥−𝑥3)
(𝑥1−𝑥0)(𝑥1−𝑥2)(𝑥1−𝑥3)
𝑦1 +
(𝑥−𝑥0)(𝑥−𝑥1)(𝑥−𝑥3)
(𝑥2−𝑥0)(𝑥2−𝑥1)(𝑥2−𝑥3)
𝑦2 +
(𝑥−𝑥0)(𝑥−𝑥1)(𝑥−𝑥2)
(𝑥3−𝑥0)(𝑥3−𝑥1)(𝑥3−𝑥2)
𝑦3
=
(3−2.75)(3−3.30)(3−3.60)
(2.35−2.75)(2.35−3.30)(2.35−3.60)
25 +
(3−2.35)(3−3.30)(3−3.60)
(2.75−2.35)(2.75−3.30)(2.75−3.60)
43 +
(3−2.35)(3−2.75)(3−3.60)
3.30−2.35 3.30−2.75 (3.30−3.60)
66 +
(3−2.35)(3−2.75)(3−3.30)
(3.60−2.35)(3.60−2.75)(3.60−3.30)
70
= −2.37 + 26.90 + 41.05 −10.71
= 54.87 KN

41. Matrix

42. Problem-8: Solve the following equations by Gauss-Jordan Elimination method.
x + y + z = 5
2x + 3y +5z = 8
4x +5z = 2
Solution: The augmented matrix =
=
=
1 1 1 5
2 3 5 8
4 0 5 2
1 1 1 5
0 1 3 -2
4 0 5 2
𝑅2
′
= 𝑅2- 2𝑅1
1 1 1 5
0 1 3 -2
0 4 -1 18
𝑅3
′
= 4𝑅1- 𝑅3

43. 1 1 1 5
0 1 3 -2
0 4 -1 18
𝑅3
′
= 4𝑅1- 𝑅3
1 1 1 5
0 1 3 -2
0 0 13 -26
𝑅3
′
= 4𝑅2- 𝑅3
1 1 1 5
0 1 3 -2
0 0 1 -2
13z = -26
=> Z = -2
𝑅2
′
= 𝑅2- 3𝑅3
=
1 1 1 5
0 1 0 4
0 0 1 -2
=
=
=
𝑅1
′
= 𝑅1 - 𝑅2- 𝑅3
1 0 0 3
0 1 0 4
0 0 1 -2
=

44. Example: Solve the following equations by Gauss-Jordan Elimination method.
5x + 2y + 3z = 1
2x + 2y = 7
8y + 7z = 14
Solution: The augmented matrix =
=
=
5 2 3 1
2 2 0 7
0 8 7 14
1 -2 3 -13
2 2 0 7
0 8 7 14
𝑅1
′
= 𝑅1- 2𝑅2
𝑅2
′
= 𝑅2- 2𝑅1
1 -2 3 -13
0 6 -6 33
0 8 7 14

45. 𝑅2
′
= 1/6𝑅2
𝑅3
′
= 𝑅3- 8𝑅2
15z = -30
=> Z = -2
=
=
=
=
𝑅1
′
= 𝑅1 + 2𝑅2 -3𝑅3
1 -2 3 -13
0 6 -6 33
0 8 7 14
1 -2 3 -13
0 1 -1 5.5
0 8 7 14
1 -2 3 -13
0 1 -1 5.5
0 0 15 -30
1 -2 3 -13
0 1 -1 5.5
0 0 1 -2
=
1 -2 3 -13
0 1 0 3.5
0 0 1 -2
=
1 0 0 0
0 1 0 3.5
0 0 1 -2
𝑅2
′
= 𝑅2+ 𝑅3

46. Example: Solve the following equations by Gauss-Jordan Elimination method.
x + 3y + 6z = 12
2x + 3y = 16
x + 9z = 14
Solution: x = 8, y = 0, z = 2/3

47. Problem-9: Find whether the following system is consistent or not.
x - 4y + 5z = 8
3x + 7y - z = 3
x + 15y -11z = -14
Solution: Forming the matrix, A=
Now, A = 0 and ≠ 0.
r (A) = 2
1 -4 5
3 7 -1
1 15 -11
1 -4
3 7


48. Forming the augmented matrix, (A,b)=
Determinant of = 31≠ 0.
r (A,b) = 3
When, r (A,b) ≥ r(A), the equation will be inconsistence (No solution).
As, r(A) < r (A,b) ;
Hence the system is inconsistence.
1 -4 5 8
3 7 -1 3
1 15 -11 -14
-4 5 8
7 -1 3
15 -11 -14

49. Curve Fitting

50. Problem-10: In a laboratory the data of water demand with respect to population
is shown in the following table .
Population (thousand) 2.10 6.22 7.17 10.52 13.68
Water Demand (cumec) 2.90 3.83 5.98 5.71 7.74
Fit a straight line from this data to find the discharge for any corresponding area
using least square method.
Linear Curve Fitting

51. Solution:
i x y 𝑥2
xy
1 2.10 2.90 4.41 6.09
2 6.22 3.83 38.69 23.83
3 7.17 5.98 51.40 42.90
4 10.52 5.71 110.67 60.10
5 13.68 7.74 187.14 105.88
∑ 39.69 26.16 392.30 238.74
m𝑎0 + 𝑎1∑𝑥𝑖 = ∑𝑦𝑖 ………..(1)
𝑎0∑𝑥𝑖 + 𝑎1 ∑𝑥𝑖
2
= ∑𝑥𝑖 𝑦𝑖 ………..(2)
From eq (1), 5 𝑎0 + 39.69 𝑎1 = 26.16
From eq (2), 39.69 𝑎0 + 392.30 𝑎1 = 238.74
Solving the equation, 𝑎0 = 2.04 & 𝑎1 = 0.402
⸫ y = 𝑎0 + 𝑎1x = 2.04 + 0.402x

52. Non-Linear Curve Fitting
Problem-11: In a laboratory the deformation (mm) of a pre-stressed cantilever
beam with respect to distance (m) from the fixed support is shown below:
Fit a parabolic curve line from this data to find the deflection for any point from
the fixed support.
2
12
10
8
6
4
0.01
0.36
0.29
0.22
0.18
0.09

53. Solution:
i x y 𝑥2 𝑥3 𝑥4 xy 𝑥2y
1 2 0.01 4 8 16 0.02 0.04
2 4 0.09 16 64 256 0.36 1.44
3 6 0.18 36 216 1296 1.08 6.48
4 8 0.22 64 512 4096 1.76 14.08
5 10 0.29 100 1000 10000 2.90 29.00
6 12 0.36 144 1728 20736 4.32 51.84
∑ 42 1.15 364 3528 36400 10.44 102.88
m𝑎0 + 𝑎1∑𝑥𝑖 + 𝑎2 ∑𝑥𝑖
2 = ∑𝑦𝑖 ………..(1)
𝑎0∑𝑥𝑖 + 𝑎1 ∑𝑥𝑖
2
+ 𝑎2 ∑𝑥𝑖
3
= ∑𝑥𝑖 𝑦𝑖 ………..(2)
𝑎0∑ 𝑥𝑖
2
+ 𝑎1 ∑𝑥𝑖
3
+ 𝑎2 ∑𝑥𝑖
4
= ∑𝑥𝑖
2
𝑦𝑖 ………..(3)

54. From eq (1), 6 𝑎0 + 42 𝑎1 + 364 𝑎2 = 1.15
From eq (2), 42 𝑎0 + 364 𝑎1 + 3528 𝑎2 = 10.44
From eq (3), 364 𝑎0 + 3528 𝑎1 + 36400 𝑎2 = 102.88
Solving the equation, 𝑎0 = -0.069, 𝑎1 = 0.042 & 𝑎2 = -5.803 x 10−4
⸫ y = 𝑎0 + 𝑎1x + 𝑎2 𝑥2 = -0.069 + 0.042 x + -5.803 x 10−4 𝑥2
Distance (m) 2 4 6 8 10 12
Deflection (mm)
y = -0.069 + 0.042 x + -5.803 x 10−4
𝑥2
0.01 0.10 0.18 0.27 0.35 0.43
Original Value(mm) 0.01 0.09 0.18 0.22 0.29 0.36

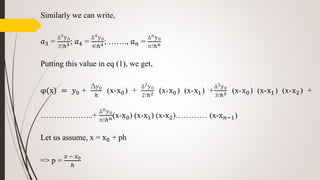
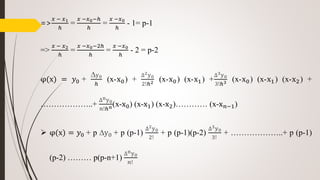
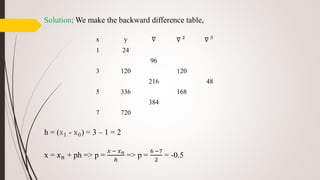
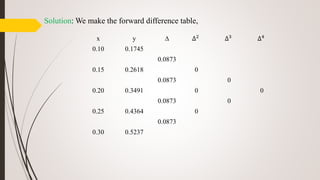
55. Problem-12: Use 4 segment to calculate the are of a function f(x) = 0.2 + 25 x +
3𝑥2 + 2𝑥4 from a = 0 to b = 2 by using Trapezoidal rule and Simpson's rule and
determine percentage of error.
Solution: For four segment n = 4. So, the value of x will be 0.5, 1.0, 1.5, 2.0.
Using Trapezoidal rules,
0
2
𝑦𝑑𝑥 =
ℎ
2
[𝑦0+ 𝑦𝑛 + 2 (𝑦1 +……..+ 𝑦(𝑛−1))]
=
0.5
2
[ 0.2 + 94.2 + 2(13.575 + 30.2 + 54.575)] = 72.775 unit
x 0 0.5 1.0 1.5 2.0
y 0.2 13.575 30.2 54.575 94.2

56. Using Simpson’s rules,
0
2
𝑦𝑑𝑥 =
ℎ
3
[𝑦0+ 𝑦𝑛 + 4 (𝑦1 + 𝑦3 + 𝑦5 +……..+ 𝑦(𝑛−1)) + 2 (𝑦2 + 𝑦4 + 𝑦6 +
……..+ 𝑦(𝑛−2))]
=
0.5
3
[ 0.2 + 94.2 + 4(13.575 + 54.575) + 2 (30.2)] = 71.23 unit
Actual area by integration method,
0
2
𝑦𝑑𝑥 = 0
2
(0.2 + 25 x + 3𝑥2 + 2𝑥4)𝑑𝑥
= 0.2x + 25
𝑥2
2
+ 3
𝑥3
3
+ 2
𝑥5
5 0
2
= 71.2 unit
Percentage of error for Trapezoidal rule =
72.775 −71.2
71.2
x 100% = 2.21%
Percentage of error for Simpson’s rule =
721.23 −71.2
71.2
x 100% = 0.042%

57. Problem-13: A irrigation reservoir discharging through sluice at a depth h, below the
water surface as a surface area A, for various value of h as given below:
If t denotes the time in min & the rate of fall of the surface is given by
𝑑ℎ
𝑑𝑡
= -
48
𝐴
ℎ , estimate the time taken for the water level to fall from 14 ft to 10 ft above
the sluice.
Solution: Area of the water reservoir, A =
ℎ
2
[ 950 + 1530 + 2 (1070 + 1200 + 1350)]
= 4860 𝑓𝑡2
h (ft) 10 11 12 13 14
A (𝑓𝑡2
) 950 1070 1200 1350 1530

58. 𝑑ℎ
𝑑𝑡
= -
48
𝐴
ℎ

𝑑ℎ
ℎ
1
2
= -
48
𝐴
dt
 10
14
ℎ−1
2 𝑑ℎ = -
48
𝐴 0
𝑡
𝑑𝑡
 [
ℎ
1
2
1
2
]
10
14
= -
48
4860
t
 t =
4860
48
x
0.58
1
2
= 117.45 min.