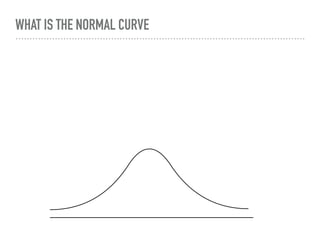
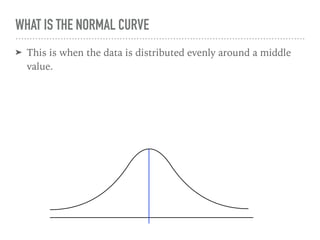
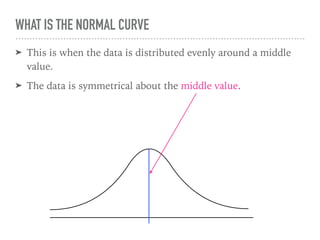
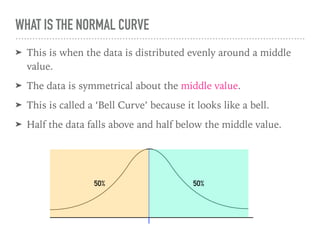
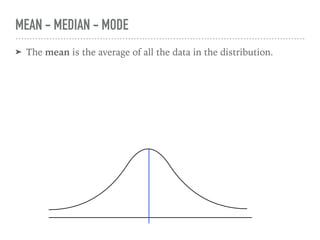
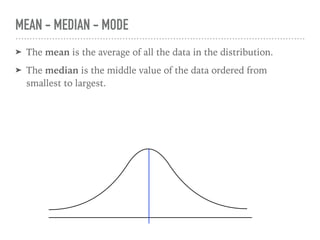
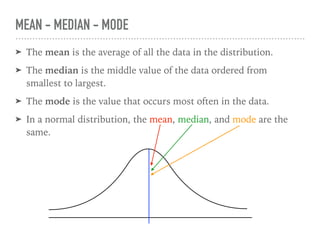
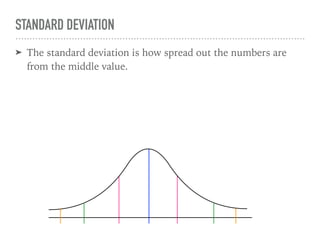
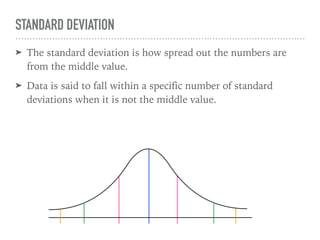
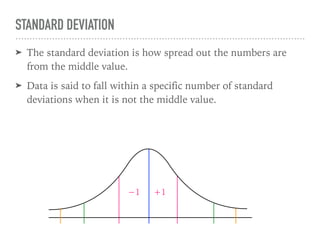
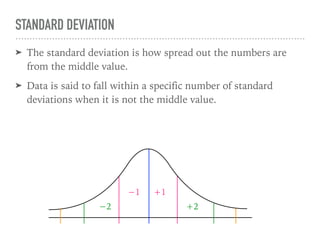
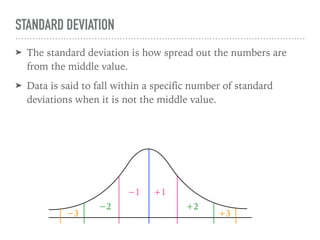
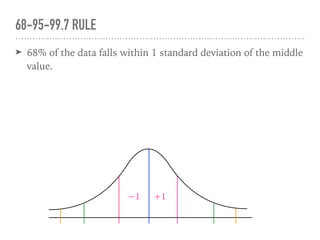
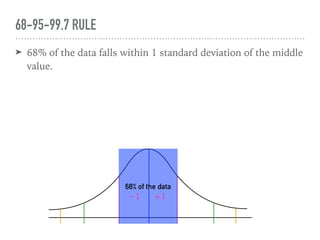
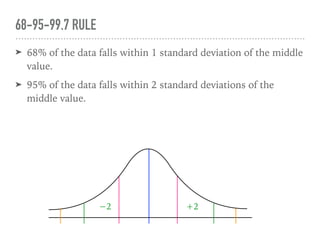
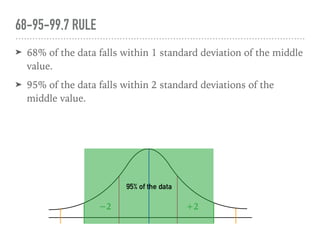
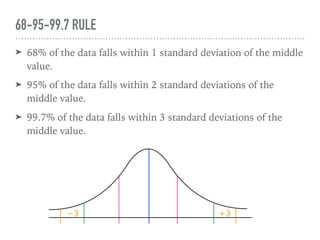
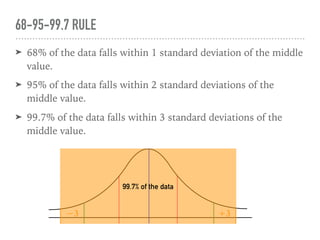
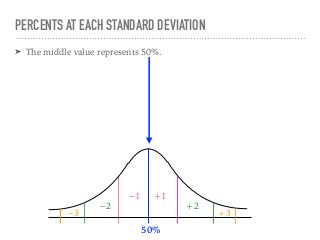
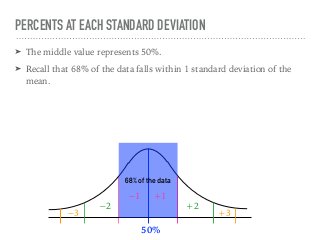
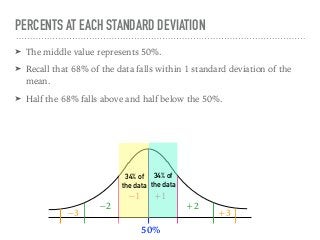
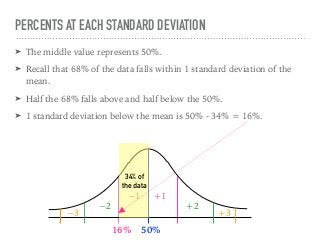
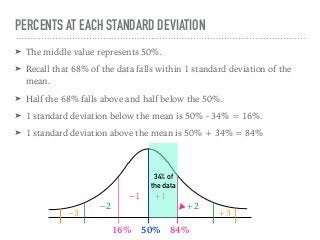
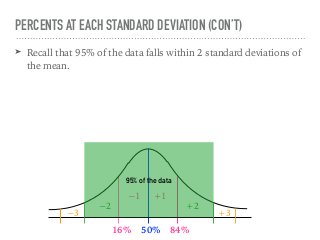
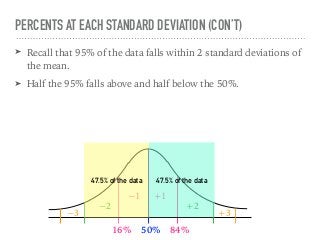
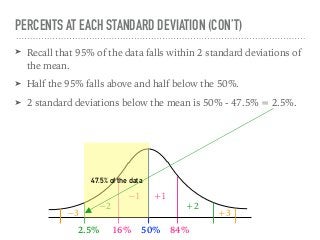
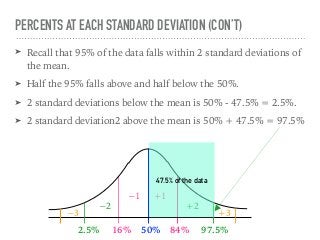
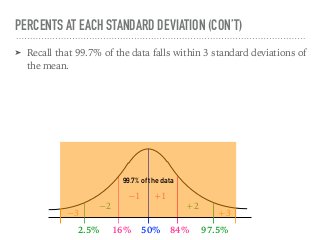
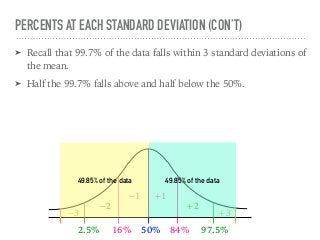
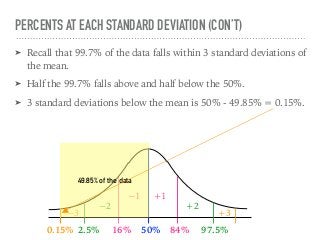
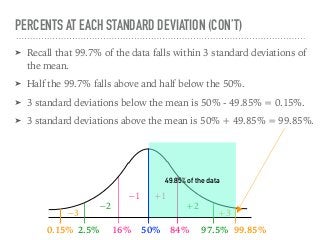
The document discusses the normal curve and its key properties. A normal curve is a bell-shaped distribution that is symmetrical around the mean value, with half of the data falling above and half below the mean. The standard deviation measures how spread out the data is from the mean. In a normal distribution, 68% of the data lies within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations, following the 68-95-99.7 rule.

1. NORMAL CURVE

2. WHAT IS THE NORMAL CURVE

3. WHAT IS THE NORMAL CURVE
➤ This is when the data is distributed evenly around a middle
value.

4. WHAT IS THE NORMAL CURVE
➤ This is when the data is distributed evenly around a middle
value.
➤ The data is symmetrical about the middle value.

5. WHAT IS THE NORMAL CURVE
➤ This is when the data is distributed evenly around a middle
value.
➤ The data is symmetrical about the middle value.
➤ This is called a ‘Bell Curve’ because it looks like a bell.
Bell by casino is licensed by Public Domain.

6. WHAT IS THE NORMAL CURVE
➤ This is when the data is distributed evenly around a middle
value.
➤ The data is symmetrical about the middle value.
➤ This is called a ‘Bell Curve’ because it looks like a bell.
➤ Half the data falls above and half below the middle value.
50% 50%

7. MEAN - MEDIAN - MODE

8. ➤ The mean is the average of all the data in the distribution.
MEAN - MEDIAN - MODE

9. ➤ The mean is the average of all the data in the distribution.
➤ The median is the middle value of the data ordered from
smallest to largest.
MEAN - MEDIAN - MODE

10. ➤ The mean is the average of all the data in the distribution.
➤ The median is the middle value of the data ordered from
smallest to largest.
➤ The mode is the value that occurs most often in the data.
MEAN - MEDIAN - MODE

11. ➤ The mean is the average of all the data in the distribution.
➤ The median is the middle value of the data ordered from
smallest to largest.
➤ The mode is the value that occurs most often in the data.
➤ In a normal distribution, the mean, median, and mode are the
same.
MEAN - MEDIAN - MODE

12. STANDARD DEVIATION

13. ➤ The standard deviation is how spread out the numbers are
from the middle value.
STANDARD DEVIATION

14. ➤ The standard deviation is how spread out the numbers are
from the middle value.
➤ Data is said to fall within a specific number of standard
deviations when it is not the middle value.
STANDARD DEVIATION

15. ➤ The standard deviation is how spread out the numbers are
from the middle value.
➤ Data is said to fall within a specific number of standard
deviations when it is not the middle value.
STANDARD DEVIATION
+1−1

16. ➤ The standard deviation is how spread out the numbers are
from the middle value.
➤ Data is said to fall within a specific number of standard
deviations when it is not the middle value.
STANDARD DEVIATION
+1−1
+2−2

17. ➤ The standard deviation is how spread out the numbers are
from the middle value.
➤ Data is said to fall within a specific number of standard
deviations when it is not the middle value.
STANDARD DEVIATION
+1−1
+2−2
+3−3

18. ➤ The standard deviation is how spread out the numbers are
from the middle value.
➤ Data is said to fall within a specific number of standard
deviations when it is not the middle value.
➤ A normal distribution follows the 68-95-99.7 rule.
STANDARD DEVIATION
+1−1
+2−2
+3−3

19. 68-95-99.7 RULE

20. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
68-95-99.7 RULE
+1−1

21. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
68-95-99.7 RULE
68% of the data
+1−1

22. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
➤ 95% of the data falls within 2 standard deviations of the
middle value.
68-95-99.7 RULE
+2−2

23. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
➤ 95% of the data falls within 2 standard deviations of the
middle value.
68-95-99.7 RULE
95% of the data
+2−2

24. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
➤ 95% of the data falls within 2 standard deviations of the
middle value.
➤ 99.7% of the data falls within 3 standard deviations of the
middle value.
68-95-99.7 RULE
+3−3

25. ➤ 68% of the data falls within 1 standard deviation of the middle
value.
➤ 95% of the data falls within 2 standard deviations of the
middle value.
➤ 99.7% of the data falls within 3 standard deviations of the
middle value.
68-95-99.7 RULE
99.7% of the data
+3−3

26. ➤ The middle value represents 50%.
PERCENTS AT EACH STANDARD DEVIATION
+1−1
+2−2
+3−3
50%

27. ➤ The middle value represents 50%.
➤ Recall that 68% of the data falls within 1 standard deviation of the
mean.
PERCENTS AT EACH STANDARD DEVIATION
68% of the data
+1−1
+2−2
+3−3
50%

28. ➤ The middle value represents 50%.
➤ Recall that 68% of the data falls within 1 standard deviation of the
mean.
➤ Half the 68% falls above and half below the 50%.
PERCENTS AT EACH STANDARD DEVIATION
+1−1
+2−2
+3−3
50%
34% of
the data
34% of
the data

29. ➤ The middle value represents 50%.
➤ Recall that 68% of the data falls within 1 standard deviation of the
mean.
➤ Half the 68% falls above and half below the 50%.
➤ 1 standard deviation below the mean is 50% - 34% = 16%.
PERCENTS AT EACH STANDARD DEVIATION
+1−1
+2−2
+3−3
50%
34% of
the data
16%

30. ➤ The middle value represents 50%.
➤ Recall that 68% of the data falls within 1 standard deviation of the
mean.
➤ Half the 68% falls above and half below the 50%.
➤ 1 standard deviation below the mean is 50% - 34% = 16%.
➤ 1 standard deviation above the mean is 50% + 34% = 84%
PERCENTS AT EACH STANDARD DEVIATION
+1−1
+2−2
+3−3
50%16% 84%
34% of
the data

31. ➤ Recall that 95% of the data falls within 2 standard deviations of
the mean.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%16% 84%
95% of the data

32. ➤ Recall that 95% of the data falls within 2 standard deviations of
the mean.
➤ Half the 95% falls above and half below the 50%.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%
47.5% of the data 47.5% of the data
16% 84%

33. ➤ Recall that 95% of the data falls within 2 standard deviations of
the mean.
➤ Half the 95% falls above and half below the 50%.
➤ 2 standard deviations below the mean is 50% - 47.5% = 2.5%.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%
47.5% of the data
16% 84%2.5%

34. ➤ Recall that 95% of the data falls within 2 standard deviations of
the mean.
➤ Half the 95% falls above and half below the 50%.
➤ 2 standard deviations below the mean is 50% - 47.5% = 2.5%.
➤ 2 standard deviation2 above the mean is 50% + 47.5% = 97.5%
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%16% 84%
47.5% of the data
2.5% 97.5%

35. ➤ Recall that 99.7% of the data falls within 3 standard deviations of
the mean.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%16% 84%2.5% 97.5%
99.7% of the data

36. ➤ Recall that 99.7% of the data falls within 3 standard deviations of
the mean.
➤ Half the 99.7% falls above and half below the 50%.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%
49.85% of the data 49.85% of the data
16% 84%2.5% 97.5%

37. ➤ Recall that 99.7% of the data falls within 3 standard deviations of
the mean.
➤ Half the 99.7% falls above and half below the 50%.
➤ 3 standard deviations below the mean is 50% - 49.85% = 0.15%.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%
49.85% of the data
16% 84%2.5% 97.5%0.15%

38. ➤ Recall that 99.7% of the data falls within 3 standard deviations of
the mean.
➤ Half the 99.7% falls above and half below the 50%.
➤ 3 standard deviations below the mean is 50% - 49.85% = 0.15%.
➤ 3 standard deviations above the mean is 50% + 49.85% = 99.85%.
PERCENTS AT EACH STANDARD DEVIATION (CON’T)
+1−1
+2−2
+3−3
50%16% 84%
49.85% of the data
2.5% 97.5%0.15% 99.85%