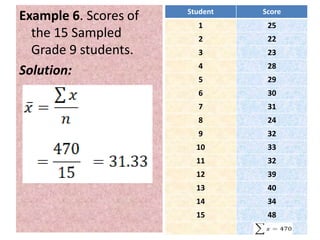
The document explains the concepts of parameters and statistics, highlighting their definitions and differences. It provides examples related to calculating population means, variances, standard deviations, sample means, sample variances, and standard deviations using both raw data and frequency distribution tables. Additionally, it includes numerous examples to illustrate these statistical methods and their application.

1. Parameter
and
Statistic

2. Learning Competency
The learner will be able to
1. Distinguish between parameter and statistic.

3. A parameter is a measure that describes a
population. It is usually denoted by Greek
letters.
A statistic is a measure that describes a
sample. It is usually denoted by Roman
letters.

4. Examples
Parameter Statistic

5. The population mean is the mean of the entire
population. It is computed using the formula:

6. Example 1. The numbers of workers in six
outlets of a fast food restaurant are 12, 10, 11,
15, 12, and 14. Treating these data as a
population, find the population mean .

7. Solution:
The population mean is computed by summing
up all the data and dividing the sum by the
number of data N. All the data are used to find
the population mean.
Number x
1 12
2 10
3 11
4 15
5 12
6 14

8. The mean is affected by each datum. If the value
of one datum is too small in comparison with
the other data, it will lower the value of the
mean. If a datum is too big compared with the
other data, it will increase the value of the
mean.

9. Example 2. Assume that the last datum in
Example 1 is 2 instead of 14.
Number x
1 12
2 10
3 11
4 15
5 12
6 2
Solution:

10. Example 3. Assume that the last datum in
Example 1 is 30 instead of 14.
Number x
1 12
2 10
3 11
4 15
5 12
6 30
Solution:

11. Population Variance and
Population Standard
Deviation

12. Variance and standard deviation are widely used
measures of dispersion of data in research.
The population variance is the sum of the
squared deviations of each datum from the
population mean divided by the population
size N. The population standard deviation is
the square root of the population variance .

13. Formula for the Population variance
Formula for Population Standard Deviation

14. Example 4. The following are the ages of 16
Teachers at USEP-Mintal.
Compute the following:
a. Population variance
b. Population standard deviation
30 34 32 38 28 36 40 31
35 34 33 30 37 40 30 40

15. Solution:
Step1. Compute the
Step2. Compute
Step3. Squared step 2
Then compute what is asked in a and b.
30 34 32 38 28 36 40 31
35 34 33 30 37 40 30 40

16. Teacher Age (x)
1 30 30-34.25= -4.25 18.0625
2 34 34-34.25= -0.25 0.0625
3 32 32-34.25= -2.25 5.0625
4 38 38-34.25= 3.75 14.0625
5 28 28-34.25= -6.25 39.0625
6 36 36-34.25= 1.75 3.0625
7 40 40-34.25=5.75 33.0625
8 31 31-34.25= -3.25 10.5625
9 35 35-34.25=0.75 0.5625
10 34 34-34.25= -0.25 0.0625
11 33 33-3425= -1.25 1.5625
12 30 30-34.25= -4.25 18.0625
13 37 37-34.25=2.75 7.5625
14 40 40-34.25=5.75 33.0625
15 30 30-34.25= -4.25 18.0625
16 40 40-34.25= 5.75 33.0625

17. a.
b.

18. Sample Mean

19. The sample mean is the average of all the
values randomly selected from the
population. That is,

20. Example 5. The following are the ages of 16
Teachers at USEP-Mintal.
Assume that a researcher randomly selected 12
out of the 16 teachers. Assume that the
encircled data below are those that were
randomly selected. Compute the sample
mean.
30 34 32 38 28 36 40 31
35 34 33 30 37 40 30 40
30 34 32 38 28 36 40 31
35 34 33 30 37 40 30 40

21. Teacher Population Age Sampled Age (x)
1 30
2 34 34
3 32
4 38 38
5 28 28
6 36 36
7 40 40
8 31 31
9 35 35
10 34 34
11 33 33
12 30 30
13 37
14 40 40
15 30
16 40 40
Solution:

22. Example 6. Scores of
the 15 Sampled
Grade 9 students.
Solution:
Student Score
1 25
2 22
3 23
4 28
5 29
6 30
7 31
8 24
9 32
10 33
11 32
12 39
13 40
14 34
15 48

23. Sample Variance and
Sample Standard
Deviation

24. Sample Variance and
Sample Standard
Method 1 Method 2

25. Method 1
The sample variance is the sum of the squared
deviation of each data from the sample mean
divided by n-1. It uses the formula below.
The sample standard deviation s is the square root
of the sample variance given by the equation
below.

26. Example 7. Calculate the sample variance and
sample standard deviation of the 12
randomly selected data in Example 5.
Solution:
Step1. Solve for the
Step2. Solve for
Step3. Solve for the square of step 2

27. Teacher Population Age Sampled Age (x)
1 30
2 34 34 -0.92 0.8464
3 32
4 38 38 3.08 9.4864
5 28 28 -6.92 47.8864
6 36 36 1.08 1.1664
7 40 40 5.08 25.8064
8 31 31 -3.92 15.3664
9 35 35 0.08 0.0064
10 34 34 -0.92 0.8464
11 33 33 -1.92 3.6864
12 30 30 -4.92 24.2064
13 37
14 40 40 5.08 25.8064
15 30
16 40 40 5.08 25.8064

28. Sample
Variance
Sample standard
deviation

29. Example 8. The following are the scores of 8
randomly selected students in Grade 10:
Compute the following:
a. Sample mean
b. Sample variance
c. Sample standard deviation
7 8 12 15 10 11 9 and 14

30. Solution:
Step1. Solve for the
Step2. Solve for
Step3. Solve for the square of step 2

31. Number x
1 7
-3.75 14.0625
2 8
-2.75 7.5625
3 12
1.25 1.5625
4 15
4.25 18.0625
5 10
-0.75 0.5625
6 11
0.25 0.0625
7 9
-1.75 3.0625
8 14
3.25 10.5625

32. Method 2
Sample Variance
Sample Standard Deviation

33. Example 9. Calculate the sample variance and
the sample standard deviation of the data
in Example 8 Method 2.
Number x x2
1 7
49
2 8
64
3 12
144
4 15
225
5 10
100
6 11
121
7 9
81
8 14
196
Sample Variance
Sample standard
deviation
Method 2

34. Finding the Sample
Mean from a Frequency
Distribution

35. Sometimes, researchers organize and present
their data using a frequency distribution table
(FDT).
Sample mean has two methods but still produce
the same results.

36. Sample Mean
Method 1 Method 2

37. Method 1 (Sample mean)
Example 10. Find the sample mean from the
frequency distribution table below.
Scores Frequency (f)
40-42 2
43-45 5
46-48 8
49-51 12
52-54 6
55-57 4
58-60 3

38. Solution:
Scores f Class Mark (x) fx
40-42 2 41 82
43-45 5 44 220
46-48 8 47 376
49-51 12 50 600
52-54 6 53 318
55-57 4 56 224
58-60 3 59 177

39. Method 2 (sample Mean)
Example 11. Find the sample mean using
Method 2 of example 10.
Scores Frequency (f)
40-42 2
43-45 5
46-48 8
49-51 12
52-54 6
55-57 4
58-60 3

40. Solution:
Scores Class Mark (x) d f fd
40-42 41 -3 2 -6
43-45 44 -2 5 -10
46-48 47 -1 8 -8
49-51 50 0 12 0
52-54 53 1 6 6
55-57 56 2 4 8
58-60 59 3 3 9

41. Method 2 (sample mean)
Example 12. Find the sample mean of the FDT
using method 2.
Ages of Teacher at USEP-Mintal
Ages Frequency
21-25 4
26-30 7
31-35 6
36-40 10
41-45 14
46-50 9
51-55 8
56-60 2

42. Solution:
Scores Class Mark (x) d f fd
21-25 23 -3 4 -12
26-30 28 -2 7 -14
31-35 33 -1 6 -6
36-40 38 0 10 0
41-45 43 1 14 14
46-50 48 2 9 18
51-55 53 3 8 24
56-60 58 4 2 8

43. Finding the Sample
Variance & Sample
Standard Deviation
from a Frequency
Distribution

44. Sample Variance & Sample
Standard Deviation
Method 1 Method 2

45. Method 1
Example 13. The scores in Chemistry of
randomly selected Grade 10 students are
shown below. Solve for
a. Sample variance
b. Standard deviation
Scores Frequency
60-64 1
65-69 2
70-74 2
75-79 4
80-84 6
85-89 8
90-94 5
95-99 7

46. Solution:
Scores f Class
Mark (x)
fx
60-64 1 62 62 -23 529 529
65-69 2 67 134 -18 324 648
70-74 2 72 144 -13 169 338
75-79 4 77 308 -8 64 256
80-84 6 82 492 -3 9 54
85-89 8 87 696 2 4 32
90-94 5 92 460 7 49 245
95-99 7 97 679 12 144 1008

48. Method 2
Example 14. Solve for the Sample variance and
Sample standard deviation of example 13 using
Method 2.
Scores f Class Mark (x) fx fx2
60-64 1 62 62 3844
65-69 2 67 134 8978
70-74 2 72 144 10368
75-79 4 77 308 23716
80-84 6 82 492 40344
85-89 8 87 696 60552
90-94 5 92 460 42320
95-99 7 97 679 65863

50. Trivia
The 12th letter of the Greek alphabet was
derived from the Egyptian hieroglyphic symbol
for water (H2O). In the system of Greek
numerals, it has a value of 40. In statistics, it
represents the population mean.