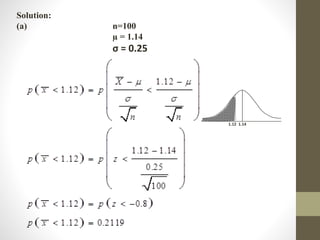
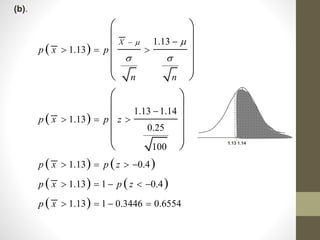
The central limit theorem states that the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, even if the population is not normally distributed. It provides the mean and standard deviation of the sampling distribution of the sample mean. The document gives the definition of the central limit theorem and provides an example of how to use it to calculate probabilities related to the sample mean of a large normally distributed population.

1. Central Limit
Theorem:
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Definition of Central Limit Theorem:
If random samples of size n are drawn
from a large or infinite population with
mean µ and variance 𝜎2
, then the
sampling distribution of the sample mean
𝑋 is approximately normally distributed
with mean µ 𝑋 = µ and standard deviation
𝜎 𝑋 =
𝜎
𝑛
.
Hence

3. Z
X
n




is a value of a standard normal variable Z.
NOTE:
Central limit theorem describes the shape of
sampling distribution of mean

4. Example-1:
A large normally distributed population has a
mean of 1.14 and standard deviation of 0.25.
A sample of size 100 is selected what is the
probability that sample mean is ;
(a) less then 1.12
(b) Greater than 1.13
(c) Between 1.15 and 1.16

6. Solution:
(a) n=100
µ = 1.14
σ = 0.25
1.12 1.14

7.  
 
   
   
 
1.13
1.13
1.13 1.14
1.13
0.25
100
1.13 0.4
1.13 1 0.4
1.13 1 0.3446 0.6554
X
p x p
n n
p x p z
p x p z
p x p z
p x
 
 
 
  

  
   
    
   
 
 
 
 
 
 
 
 
 
  1.13 1.14
(b).

8.  
 
   
     
 
1.15 1.16
1.15 1.16
1.15 1.14 1.16 1.14
1.15 1.16
0.25 0.25
100 100
1.15 1.16 0.4 0.8
1.15 1.16 0.8 0.4
1.15 1.16 0.7881 0.6554 0.1327
X
p x p
n n n
p x p z
p x p z
p x p z p z
p x
 
  
 
    
 
    
    
     
    
 
 
 
 
 
 
 
 
 
 
1.14 1.15 1.16
(c).

9. DO YOUR SELF
Q1.
If the hourly wages of workers have a mean of $
5 per hours and a standard deviation of $ 0.60,
what is the probability that the mean wage of a
random sample of 50 workers will be
(a)Less than $ 5.20 (Ans:0.9906)
(b)More than $ 4.90 (Ans:0.879)
(c)Between $ 5.10 and $ 5.20 (Ans:0.1160)

10. Q2.
The average purchase in a store has been $236
with a standard deviation of $ 48.If a random
sample of 36 sales made during period were
selected, what is the probability that the sample
mean would be
(a) Less than $ 220 (Ans:0.0228)
(b) More than $ 220 (Ans:0.9772)
(c) Between $ 215 and $ 225 (Ans:0.0809)

11. Q3.
The mean SAT scores of all students attending a
large university is 980 points with a variance 2500
points. What is the probability that the mean SAT
score of a random sample of 100 students is
(a) At most 990 points (Ans:0.9772)
(b) At least 990 points (Ans:0..0228)
(c) More than 980 and less than 995 points
(Ans0.4987)