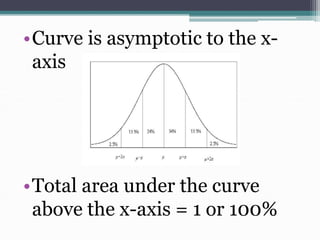
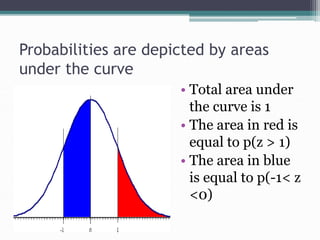
The normal distribution is a continuous probability distribution that is symmetric and bell-shaped. It is defined by its mean and standard deviation. Many real-world variables are approximately normally distributed. The standard normal distribution refers to a normal distribution with a mean of 0 and standard deviation of 1. The normal distribution is commonly used to model variables and calculate probabilities related to areas under the normal curve.

1. Normal Distribution

2. Definition
•It is defined as a continuous
frequency distribution of
infinite range.
•The normal distribution is a
descriptive model that
describes real world situations.

3. Importance
• Many dependent variables are
commonly assumed to be normally
distributed in the population
• If a variable is approximately normally
distributed we can make inferences
about values of that variable

4. Characteristics
•Bell-Shaped

5. •Mean=Median=Mode

6. •Curve is asymptotic to the x-
axis
•Total area under the curve
above the x-axis = 1 or 100%

7. Empirical Rule:
68% of
the data
95% of the data
99.7% of the data

8. •Mathematical Formula
Note constants:
=3.14159
e=2.71828
The Normal Distribution:
as mathematical function (pdf)
2
)(
2
1
2
1
)( 





x
exf
This is a bell shaped
curve with different
centers and spreads
depending on  and 

9. The Standard Normal
Distribution (Z)
•The mean (μ ) = 0
•Standard deviation (σ) =1
)1,0(~),(~ N
x
ZNX






10. 11 33

11. Probabilities are depicted by areas
under the curve
• Total area under
the curve is 1
• The area in red is
equal to p(z > 1)
• The area in blue
is equal to p(-1< z
<0)

12. Finding Areas under the Normal
Curve
•Example:
▫Find the area to the right of:
1. z= 1.25
2. z=-.34

13. •Example:
▫Find the area to the left of:
1. z=0.33
2. z=-0.21

14. •Example:
▫Find the area between:
1. z = -0.24 and z = 1.23
2. z = 0.15 and z = 2.04
3. z = -0.15 and z = -2.02

15. Applications of the Normal
Distribution
• Example:
▫ DGP University conducts placement
examination to all incoming freshmen. The
examination scores of the 1000 examinees
last semester were approximately normally
distributed with mean score of 80 and
standard deviation of 5. What is the probability
that randomly chosen student got a score
below 70?above 82? Between 75 and 90?

16. Solution: a.below 70
•Given:
▫μ= 80
▫σ =5
▫x<70



x
Z
5
8070 
Z
Z= -2

17. • P [x<70] = P[z<-2] = 0.5 – P[0<z<2]
=0.5 – 0.4772
=0.0228 or 2.28%
-2

18. Solution: above 82
5
8082 
Z = 0.4

19. • P [x>82] = P[z>0.4] = 0.5 – P[0>z>0.4]
=0.5 – 0.1554
=0.3446 or 34.46%
0.4

20. Exercise: (Using the same
problem) Sketch of the curve and
find:
•Between 75 and 90 (Ronald and Jyx,)
•How many got scores below
87? (Nikki,Dioniel ) above 77?
(Frea,Gretchel) between 75 and 90
(Vhea and Sheryl)

21. Evaluation: (1/2)
• X is a normally normally distributed
variable with mean μ = 30 and standard
deviation σ = 4. Find
a) P(x < 40)
b) P(x > 21)
c) P(30 < x < 35)

22. • Molly earned a score of 940 on a national
achievement test. The mean test score was 850
with a standard deviation of 100. What
proportion of students had a higher score than
Molly? (Assume that test scores are normally
distributed.)

23. Agreement:
•A firms marketing manager
believes that total sales for the
firm next year can be modeled
using a normal distribution, with a
mean of P 2.5 million and a
standard deviation of P300,000

24. a. What is the probability that the
firm’s sales will exceed the P3
million?
b. In order to cover fixed cost, the
firm’s sales must exceed the
break-even level of P 1.8 million.
What is the probability that sales
will exceed the break-even level?