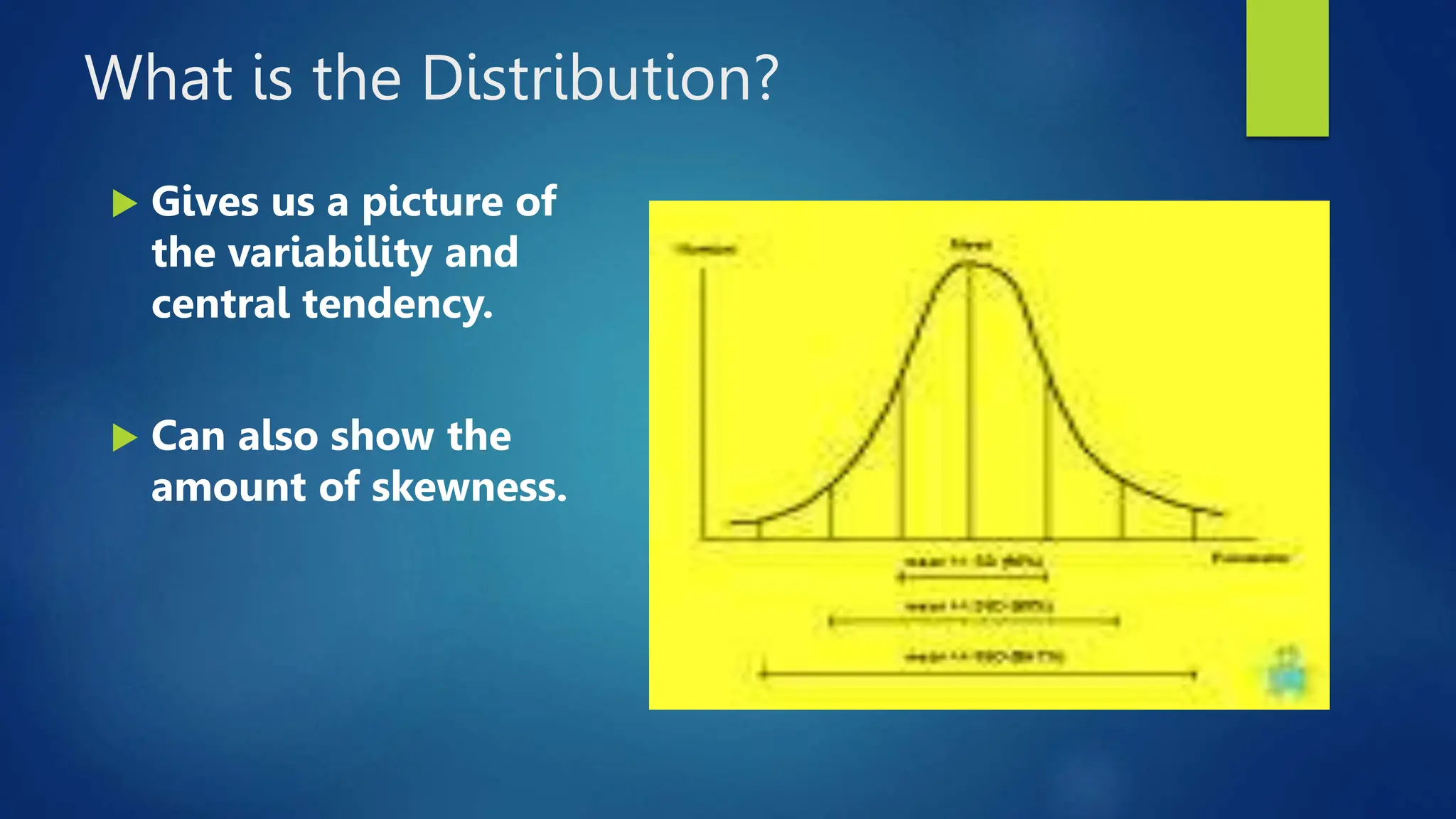
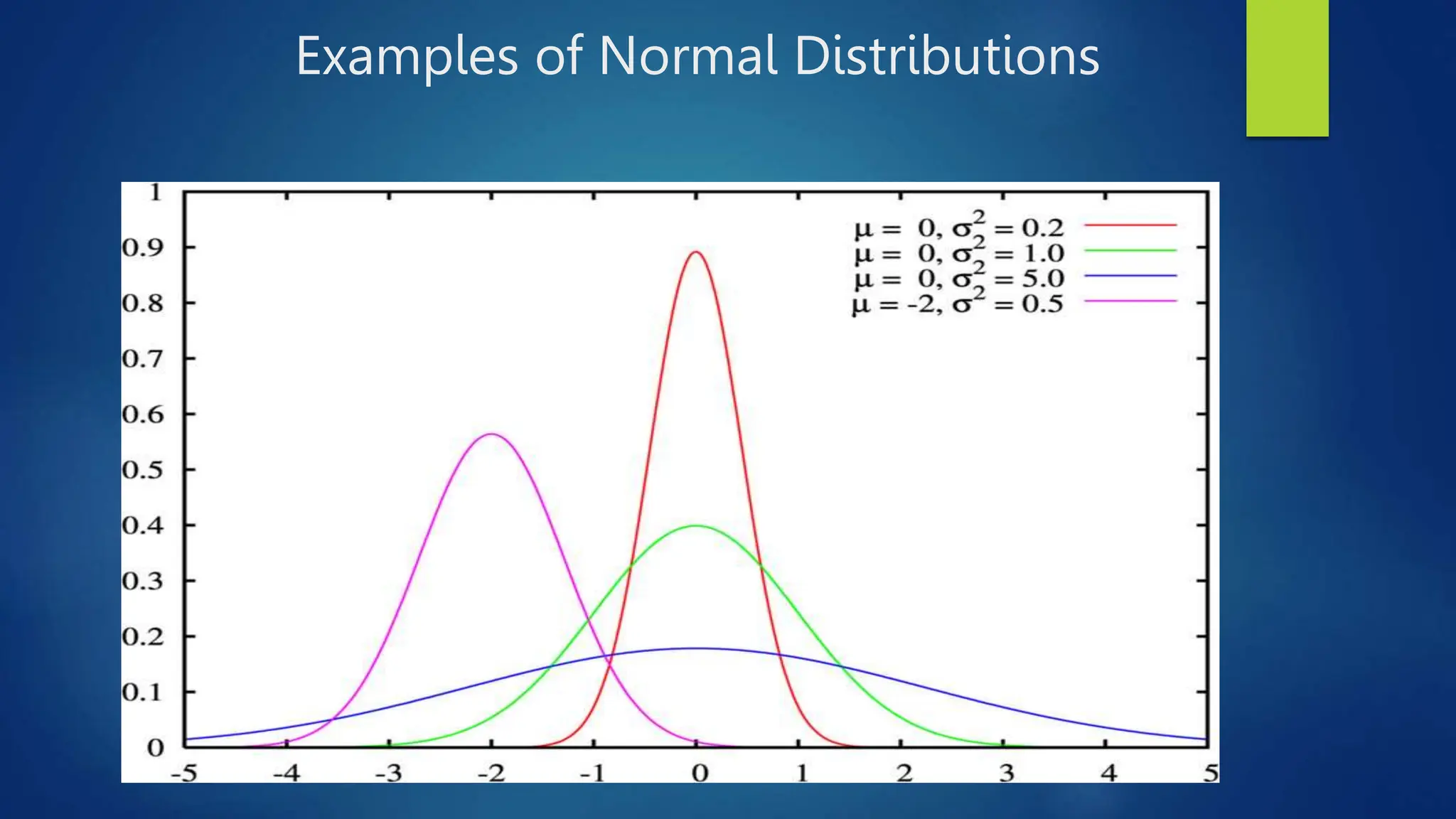
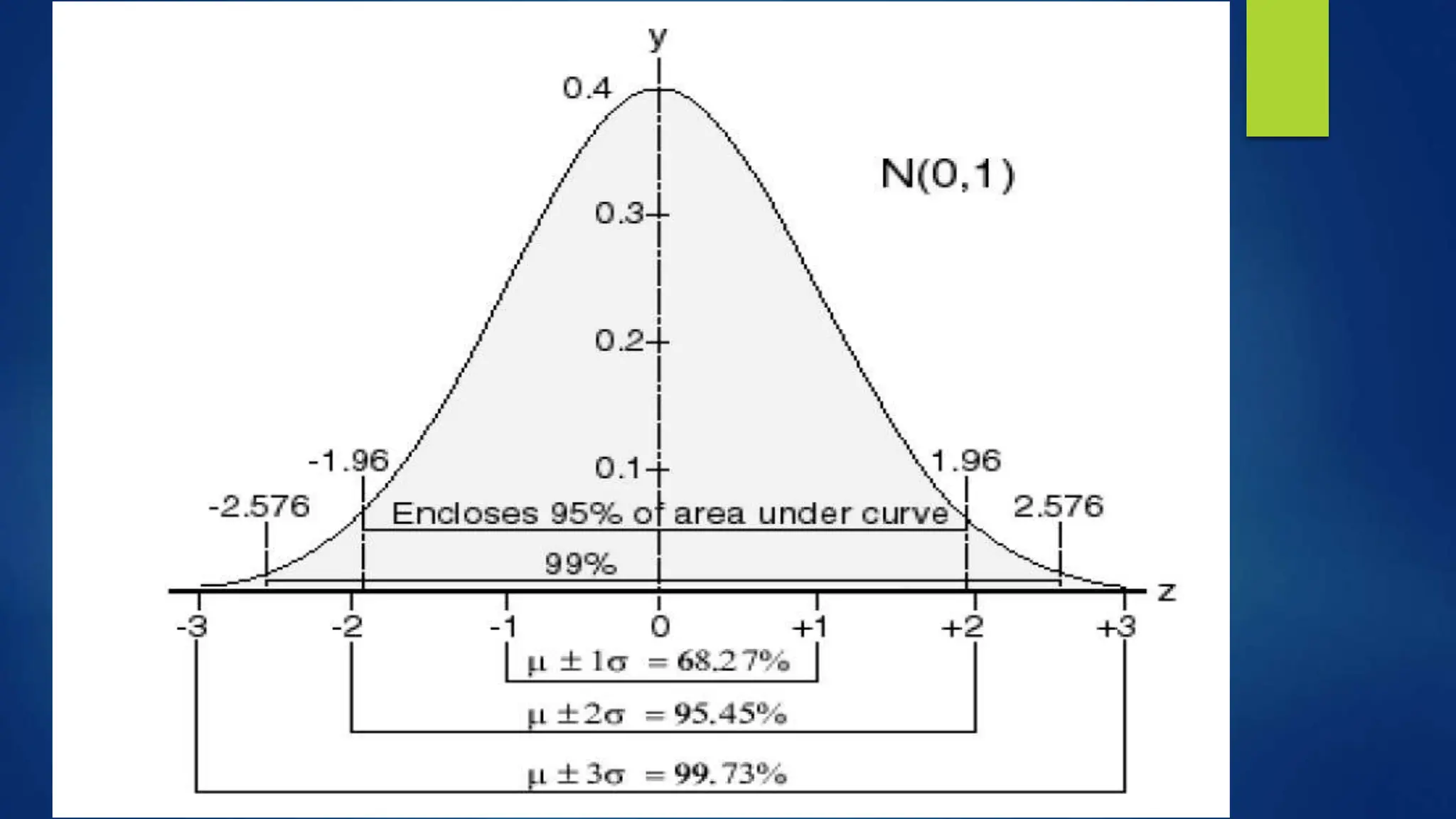
The document discusses the concepts of populations and samples in statistical analysis, emphasizing the importance of understanding sampling variation, mean estimation, and standard deviation. It highlights the role of the normal distribution, describing key characteristics and its relevance in statistical interpretation. Additionally, it explains the relationship between standard deviation, standard error, and the distribution of sample means in relation to the overall population mean.