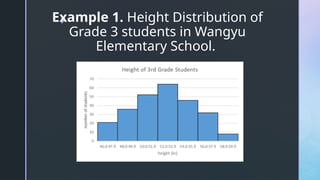
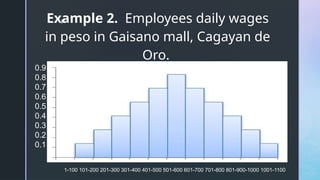
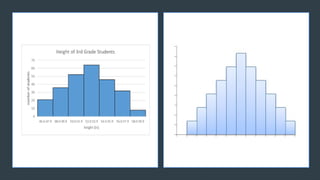
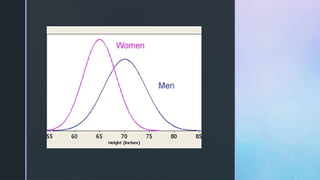
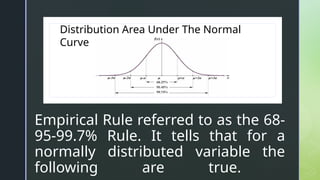
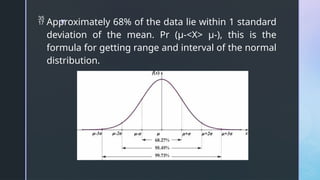
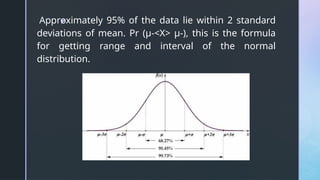
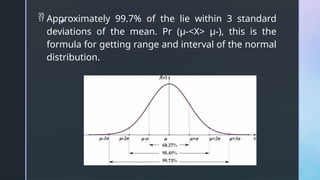
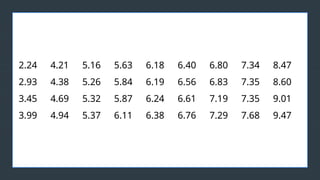
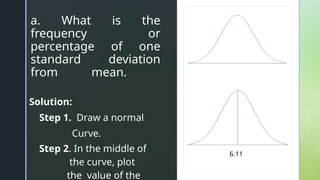
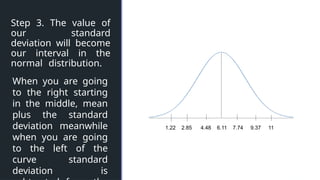
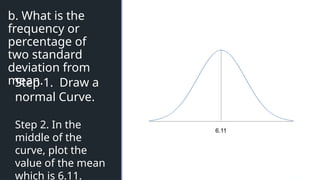
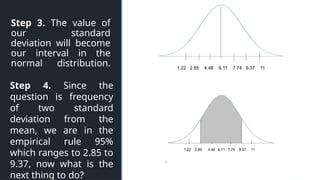
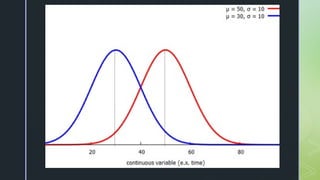
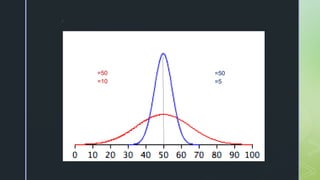
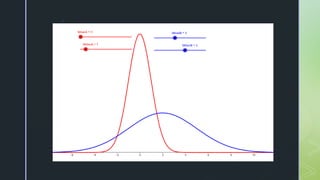
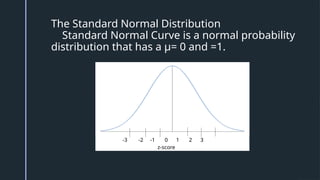
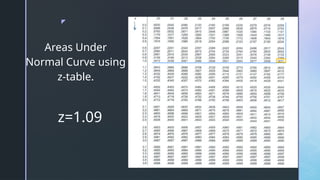
The document discusses normal distribution, including its properties and applications in statistics. It explains the empirical rule and provides examples involving the calculation of frequencies and areas under the normal curve using standard deviation and z-scores. Additionally, it includes exercises and quizzes to practice understanding and applying normal distribution concepts.

1. z
Is this
normal?

2. z
Is this
normal?
Why do you
think its not
normal?

3. z
Is this normal?
Why should we
normalize this
kind of
practice?

4. z
Is this normal?
Why should we
NOT normalize
this kind of
behavior?
NILAIT VS NANLAIT

5. z
Example 1. Height Distribution of
Grade 3 students in Wangyu
Elementary School.

6. z
Example 2. Employees daily wages
in peso in Gaisano mall, Cagayan de
Oro.
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
1-100 101-200 201-300 301-400 401-500 501-600 601-700 701-800 801-900-1000 1001-1100

7. z

8. z
N R
O
M
A
L C
U
R V
E

9. z
N
R
O M A L
C U
R
V E

10. z
Normal Distribution
is also called as
Gaussian
Distribution. It is the
probability of
continuous random
variable and
consider as the most
important curve in
statistics.

11. z
z
The
equation of
the
theoretical
normal
distribution
is given by
the formula.

12. z

13. Properties of Normal
Curve.
1.The distribution curve is
bell shaped.
2.The curve is symmetrical
to its center, the mean.
3.The mean, median and
mode coincide at the
center.

14. Properties of Normal
Curve.
3. The width of the curve is
determined by the standard
deviation of the distribution.
4. The curve is asymptotic to the
horizontal axis.
5. The area under the curve is 1, thus
it represents the probability or
proportion, or percentage associated
with specific sets of measurements
values.

15. Normal distribution is determined by
two parameters: the mean and the
standard deviation.
1. Mean Value
2. Standard Deviation Value

16. z
z
Empirical Rule referred to as the 68-
95-99.7% Rule. It tells that for a
normally distributed variable the
following are true.
Distribution Area Under The Normal
Curve

17. z
 Approximately 68% of the data lie within 1 standard
deviation of the mean. Pr (μ-<X> μ-), this is the
formula for getting range and interval of the normal
distribution.

18. z
Approximately 95% of the data lie within 2 standard
deviations of mean. Pr (μ-<X> μ-), this is the formula
for getting range and interval of the normal
distribution.

19. z
 Approximately 99.7% of the lie within 3 standard
deviations of the mean. Pr (μ-<X> μ-), this is the
formula for getting range and interval of the normal
distribution.

20. z
z
Example 1. What is the frequency
and relative frequency of babies’
weight that are within;
a. What is the frequency
or percentage of one
standard deviation from
mean.
b. What is the frequency
or percentage of two
standard deviation from
mean.
4.94 4.69 5.26 7.29 7.19 9.47 6.61 5.84 6.83
3.45 2.93 6.38 4.38 6.76 9.02 8.47 6.80 6.40
8.60 3.99 7.68 2.24 5.32 6.24 6.29 5.63 5.37
5.26 7.35 6.11 7.34 5.87 6.56 6.18 7.35 4.21

21. z

22. z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47

23. z
z
a. What is the
frequency or
percentage of one
standard deviation
from mean.
Solution:
Step 1. Draw a normal
Curve.
Step 2. In the middle of
the curve, plot
the value of the
6.11

24. z
z
Step 3. The value of
our standard
deviation will become
our interval in the
normal distribution.
1.22 2.85 4.48 6.11 7.74 9.37 11
When you are going
to the right starting
in the middle, mean
plus the standard
deviation meanwhile
when you are going
to the left of the
curve standard
deviation is

25. z Step 4. Since the question is
frequency of one standard deviation
from the mean, we are in the
empirical rule 68% which ranges to
4.48 to 7.74, now we are going to
count.

26. z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47
26 ÷ 36=72 %
÷÷

27. z
z
b. What is the
frequency or
percentage of
two standard
deviation from
mean.
6.11
Step 1. Draw a
normal Curve.
Step 2. In the
middle of the
curve, plot the
value of the mean
which is 6.11.

28. z
z
Step 3. The value of
our standard
deviation will become
our interval in the
normal distribution. 1.22 2.85 4.48 6.11 7.74 9.37 11
Step 4. Since the
question is frequency
of two standard
deviation from the
mean, we are in the
empirical rule 95%
which ranges to 2.85 to
9.37, now what is the
next thing to do?

29. z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47
3 4 ÷ 36=95 %
÷÷

30. z
How about if we
compare two data
sets with normal
curve?

31. z

32. z
=50
=10
=50
=5

33. z

34. z
z
The Standard Normal Distribution
Standard Normal Curve is a normal probability
distribution that has a μ= 0 and =1.
-3 -2 -1 0 1 2 3
z-score

35. z The letter Z is used to denote
the standard normal random
variable. The specific value of
the random variable z is
called the z-score. The Table
of Area Under the Normal
Standard Curve is also known
as the Z-table. It is where you
are going to look for the
value of random variable z or

36. z
Areas Under
Normal Curve using
z-table.
z=1.09

37. z
z=0.62
z=-1.65
z=3

38. z
z
Example. Find the area between
z=0 and z=1.54.
0.4382

39. z
z
Areas Under
Standard
Normal Curve
Find the area
between z=1.52
and z=2.5

40. z
Find the area
between z= -1.5
and z=-2.5

41. z
Let’s try
this !
1. Anna is planning to enroll in MSU
taking up Bachelor of Science in Civil
Engineering. The average academic
performance of all the students 80 and
a standard deviation of 5, it follows a
normal distribution.
a. Sketch a Normal Curve using
Empirical Rule and describe the
curves.
2. Find the area between z=1.7 and z=2

42. z
Let's have a short quiz.
Instruction: Answer the following questions and
make sure your writings clear and readable.
I. Find the area under the normal curve in each
of the following cases.
1. Find the Area between z= -1.36
and z=2.25.
2. To the right of z=1.85
3. To the left z=-0.45

43. z
II. Sketch a normal curve.
1. Mean of 15 and a standard deviation of 4.
On same axis, sketch another curve that has a
mean of 25 and a standard deviation of 4.
Describe the two random curves.
III. Essay
1. State a real-life situation that a normal
curve distribution can be used.