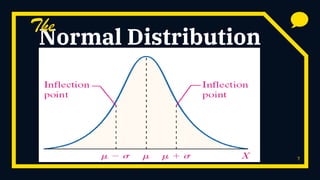
This document provides information about the normal distribution and related statistical concepts. It begins with learning objectives and definitions of key terms like the normal distribution formula and how the mean and standard deviation affect the shape of the distribution. It then discusses properties of the normal distribution like symmetry and how it extends infinitely in both directions. The next sections cover areas under the normal curve and how to calculate probabilities using the standard normal distribution table. Later sections explain how to convert variables to standard scores using z-scores and the concepts of skewness and sampling distributions. Examples and exercises are provided throughout to illustrate calculating probabilities and percentiles for the normal distribution.

1. NORMAL
DISTRIBUTION
The
Prepared by:
Maam Camille Joy G. Ramos
Mathematics Teacher

2. Learning Objectives:
The learner will be able to:
Illustrate a normal random variable and its properties;
Construct a normal curve; and
Identify regions under the normal curve corresponding
to different standard normal variables.
2

3. Normal
The normal distribution, also known as
Gaussian Distribution, has the following
formula:
3
Distribution
The
𝑷 𝒙 =
𝟏
𝝈 𝟐𝝅
𝒆
−
𝒙−𝝁 𝟐
𝟐𝝈 𝟐

4. Normal Distribution
𝒙
𝒇(𝒙)
𝝁
𝝈
Changing 𝝁 shifts the
distribution left or right.
Changing 𝝈 increases
or decreases the
spread.
The

5. 𝟔𝟖%
𝟗𝟓%
𝟗𝟗. 𝟕%
𝟔𝟖 − 𝟗𝟓 − 𝟗𝟗. 𝟕 Rule
The

6. Normal Distribution
The

7. 7
Normal Distribution
The

8. Characteristics
All normal distributions have the same shape.
Perfectly symmetric, mound-shaped distribution.
Also known as normal curve, or bell-curve.
Describes continuous random variable.
Distribution continues infinitely in both directions: both
sides of the curve are approaching zero, but they never
reach zero 0 .
8
The

9. Characteristics
Center
Located at the highest point over the mean 𝜇.
Mean, median, and mode are all equal.
Splits the data into two (2) equal parts.
Spread
Measured with standard deviation 𝜎.
Larger standard deviations mean that the data is spread
farther from the center.
9
The

10. Characteristics
Inflection Point
Curve changes shape at the inflection points: in other words,
the curve changes concavity.
A curve that is concave up looks like a u-shape.
A curve that is concave down looks like a n-shape.
The two inflection points occur ±1 standard deviation away
from the mean 𝜇 − 𝜎 𝑎𝑛𝑑 𝜇 + 𝜎 .
10
The

11. Standard
If the mean 𝝁 is zero and the standard
deviation 𝝈 is 𝟏, then the normal
distribution is a standard normal
distribution.
11
Distribution
The
Normal

12. Areas Under
Areas under the standard normal curve
can be found using the Areas under the
Standard Normal Curve table. These
areas are regions under the normal
curve.
12
the Normal
Curve

13. Areas Under
Example 1:
Find the area between 𝑧 = 0 and
𝑧 = 1.54.
13
the Normal
Curve
STEP 1: Sketch the normal curve.
STEP 2: Locate the area.

14. Areas Under
Example 2:
Find the area between 𝑧 = 1.52 and 𝑧 = 2.5.
14
the Normal
Curve
Example 3:
Find the area to the right of 𝑧 = 1.56
Example 4:
Find the area between 𝑧 = 0 and 𝑧 = −1.65.

15. Areas Under
Example 5:
Find the area between 𝑧 = −1.5 and 𝑧 = −2.5.
15
the Normal
Curve
Example 6:
Find the between 𝑧 = −1.35 and 𝑧 = 2.95.
Example 7:
Find the area to the left of 𝑧 = 2.32.

16. Areas Under
Example 8:
Find the area to the right of 𝑧 = −1.8.
16
the Normal
Curve
Example 9:
Find the area to the left of 𝑧 = −1.52.

17. Areas Under the
Exercise 1:
What percent of the area under the normal curve is between 𝑧 =
0.85 and 𝑧 = 2.5?
17
Normal Curve
Exercises:
Exercise 2:
What percent of the area under the normal curve is between 𝑧 =
− 1.00 and 𝑧 = 1.00?

18. Areas Under the
Exercise 3:
What percent of the area under the normal curve is between 𝑧 =
− 2.10 and 𝑧 = 2.10?
18
Normal Curve
Exercises:
Exercise 4:
What percent of the area under the normal curve is between 𝑧 =
− 1.10 and 𝑧 = −2.43?

19. STANDARD
SCORES

20. Learning Objectives:
The learner will be able to:
Convert a normal random variable to a standard
normal variable and vice versa; and
Compute probabilities and percentiles using the
standard normal table.
20

21. The standard score or z-score measures how many
standard deviation a given value (𝑥) is above or below the
mean.
The z-scores are useful in comparing observed values.
21
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
A positive z-score indicates that the score or observed value
is above the mean, whereas a negative z-score indicates that
the score or observed value is below the mean.

22. The standard score or z-score (For Sample)
22
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
𝑧 =
𝑥− 𝑥
𝑠
where:
𝑧: standard score
x: raw score or observed value
𝑥: sample mean
𝑠: sample standard deviation

23. The standard score or z-score (For Population)
23
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
𝑧 =
𝑥−𝜇
𝜎
where:
𝑧: standard score
x: raw score or observed value
𝜇: population mean
𝜎: population standard deviation

24. Example 1:
On a final examination in Biology, the mean was 75 and
the standard deviation was 12. Determine the standard
score of a student who received a score of 60 assuming
that the scores are normally distributed.
24
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

25. Example 2:
On the first periodic exam in Statistics, the population
mean was 70 and the population standard deviation was
9. Determine the standard score of a student who got a
score of 88 assuming that the scores are normally
distributed.
25
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

26. Example 3:
Luz scored 90 in an English test and 70 in a Physics test.
Scores in the English test have a mean of 80 and a
standard deviation of 10. Scores in the Physics test have
a mean of 60 and a standard deviation of 8. In which
subject was her standing better assuming that the scores
in her English and Physics class are normally distributed?
26
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

27. Example 4:
In a Science test, the mean score is 42 and the standard
deviation is 5. Assuming that the scores are normally
distributed, what percent of the score is
greater than 48?
less than 50?
between 30 and 48? 27
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

28. Example 5:
The mean height of grade nine students at a certain high
school is 164 centimeters and the standard deviation is
10 centimeters. Assuming that the heights are normally
distributed, what percent of the heights is greater than
168 centimeters?
28
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

29. Example 6:
In a Math test, the mean score is 45 and the standard
deviation is 4. Assuming normality, what is the probability
that a score picked at random will lie
above score 50?
below score 38?
29
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The

30. Exercise 1:
In a given normal distribution, the sample mean is 75 and
the sample standard deviation is 4. Find the
corresponding score of the following values:
1. 69 3. 70
2. 85 4. 65 30
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
Exercises:

31. Exercise 2:
In a given normal distribution, the population mean is 80
and the population standard deviation is 2.5. Find the
corresponding score of the following values:
1. 69 3. 70
2. 85 4. 65 31
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
Exercises:

32. Exercise 3:
On a test in Statistics, the mean is 65 and the standard
deviation is 3. Assuming normality, what is the standard
score of a student who receives a score of 60?
32
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
Exercises:

33. Exercise 4:
On a final examination in Mathematics, the mean was 76
and the standard deviation was 5. Determine the
standard score of a student who received a score of 88
assuming the scores are normally distributed.
33
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
Exercises:

34. Exercise 5:
In an English test, the mean is 60 and the standard
deviation is 6. Assuming the scores are normally
distributed, what percent of the scores is:
greater than 65? between 50 and 65?
less than 70? 34
Standard Score (𝑧 − 𝑠𝑐𝑜𝑟𝑒)
The
Exercises:

35. SKEWNESS

36. Skewness
A distribution is said to be symmetric
if the mean, median, and mode occur at
the same point. The curve is bell-
shaped.
36

37. Skewness
Skewness is the degree of departure
from the symmetry of a distribution.
37

38. Skewness
If the mean, median, and mode are
not at the same point, then the
frequency distribution is asymmetrical.
A distribution of this sort graphed has a
longer tail on one side than the other
side.
38

39. SkewnessA distribution with longer tail on the
left is said to be skewed to the left or
negatively skewed.
A distribution with longer tail on the
right than the left is said to be skewed to
the right or positively skewed.
39

40. 40
That’s all, folks!
Any questions?
Ask now or you’ll regret this for the rest of your life!

41. SAMPLINGand
SAMPLING
DISTRIBUTIONS

42. Learning Objectives:
The learner will be able to:
Illustrate a random sampling.
42

43. Random
A researcher always wishes to achieve
unbiased results in his or her study. One
of the best ways to fulfill this through the
use of random sampling.
43
Sampling
There are four (𝟒) types of random
sampling techniques.

44. Random
44
Sampling
1. Simple Random Sampling (SRS)
2. Systematic Sampling
3. Stratified Sampling
4.Cluster or Area Sampling
Types of

45. Random Sampling
45
This is the most basic sampling technique.
In this sampling technique, every member of the population
has an equal chance of being chosen to be part of the sample.
Ways to do simple random sampling:
1. Table of Random Numbers
2. Lottery Method
Also known as Simple Random Sampling without Replacement
(SRSWOR) and Simple Random Sampling with Replacement
(SRSWR)
Simple
Table of
Random
Numbers

46. Random
46
Sampling
Simple
DEFINITION OF SIMPLE RANDOM SAMPLING
A simple random sampling is a sampling
technique in which every element of the
population has the same probability of being
selected for inclusion in the sample.

47. 47
Random Sampling
This is a random sampling technique in which every 𝑘 𝑡ℎ
element of
the population is selected until the desired number of elements in
the sample is obtained. The value of 𝑘 is calculated by dividing the
number of elements in the population by the number of elements in
the desired sample. The value of 𝑘 is the sampling interval.
𝒌 =
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝒕𝒉𝒆 𝒑𝒐𝒑𝒖𝒍𝒂𝒕𝒊𝒐𝒏
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝒕𝒉𝒆 𝒔𝒂𝒎𝒑𝒍𝒆
𝒌 =
𝑵
𝒏
Systematic
𝑤ℎ𝑒𝑟𝑒: 𝑘 = 𝑠𝑎𝑚𝑝𝑙𝑒 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙
𝑁 = 𝑝𝑜𝑝𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑖𝑧𝑒
𝑛 = 𝑠𝑎𝑚𝑝𝑙𝑒 𝑠𝑖𝑧𝑒

48. 48
Random Sampling
A systematic sampling is a random sampling
technique in which a list of elements of the
population is used as sampling frame and the
elements to be included in the desired sample
are selected by skipping through the list at
regular intervals.
Systematic
DEFINITION OF SYSTEMATIC RANDOM SAMPLING

49. 49
In stratified sampling, the population is partitioned
into several subgroups called strata, based on some
characteristics like year level, gender, age, ethnicity,
etc.
Random Sampling
Stratified

50. 50
Stratified Sampling is a random sampling technique in
which the population is first divided into strata and
then samples are randomly selected separately from
each stratum.
Random Sampling
Stratified
DEFINITION OF STRATIFIED RANDOM SAMPLING

51. 51
Cluster or area sampling is a random sampling technique in
which the entire population is broken into small groups or
clusters, and then, some of the clusters are randomly
selected. The data from the randomly selected clusters are
the ones that are analyzed.
Random Sampling
Cluster or Area
DEFINITION OF CLUSTER OR AREA RANDOM SAMPLING

52. 52
The difference of cluster sampling from a stratified sampling
is that the sample consists of elements from the selected
clusters only while in stratified sampling, the sample consist
of elements from all the strata.
Random Sampling
Cluster or Area
DEFINITION OF CLUSTER OR AREA RANDOM SAMPLING

53. 53
The difference of cluster sampling from a stratified sampling
is that the sample consists of elements from the selected
clusters only while in stratified sampling, the sample consist
of elements from all the strata.
Random Sampling
Cluster or Area
DEFINITION OF CLUSTER OR AREA RANDOM SAMPLING

54. 54
1. The office clerk gave the researcher a list of 500 Grade 10
students. The researcher selected every 20 𝑡ℎ
name on the
list.
2. In a recent research that was conducted in a private
school, the subjects of the study were selected by using the
Table of Random Numbers.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
SYSTEMATIC RANDOM SAMPLING
SIMPLE RANDOM SAMPLING

55. 55
3. A researcher interviewed people from each town in the
province of Albay for his research on population.
4. A researcher is doing a research work on the students’
reaction to the newly implemented curriculum in
Mathematics and interviewed every 10 𝑡ℎ student entering
gate of the school.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
CLUSTER OR AREA RANDOM SAMPLING
SYSTEMATIC RANDOM SAMPLING

56. 56
5. A researcher who is studying the effects of educational
attainment on promotion conducted a survey of 50 randomly
selected workers from each of these categories: high school
graduate, with undergraduate degrees, with master’s
degree, and with doctoral degree.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
STRATIFIED RANDOM SAMPLING

57. 57
6. A researcher selected a sample of 𝑛 = 120 from a
population of 850 by using the Table of Random Numbers.
7. A researcher interviewed all top 10 Grade 11 students in
each of 15 randomly selected private schools in Metro
Manila.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
SIMPLE RANDOM SAMPLING
CLUSTER OR AREA RANDOM SAMPLING

58. 58
8. A teacher asked her students to fall in line. He instructed
one of them to select every 5 𝑡ℎ
student on the line.
9. A researcher surveyed all diabetic patients in each of the
25 randomly selected hospitals in Metro Manila.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
SYSTEMATIC RANDOM SAMPLING
CLUSTER OR AREA RANDOM SAMPLING

59. 59
10. A teacher who is conducting a research on the effects of
using calculators in teaching Mathematics decided to divide
her students into male and female and then she selected
students from each gender group.
Random Sampling
Identify what type of
Instruction: Identify the type of sampling technique used by the
researcher in each of the following situations.
STRATIFIED RANDOM SAMPLING