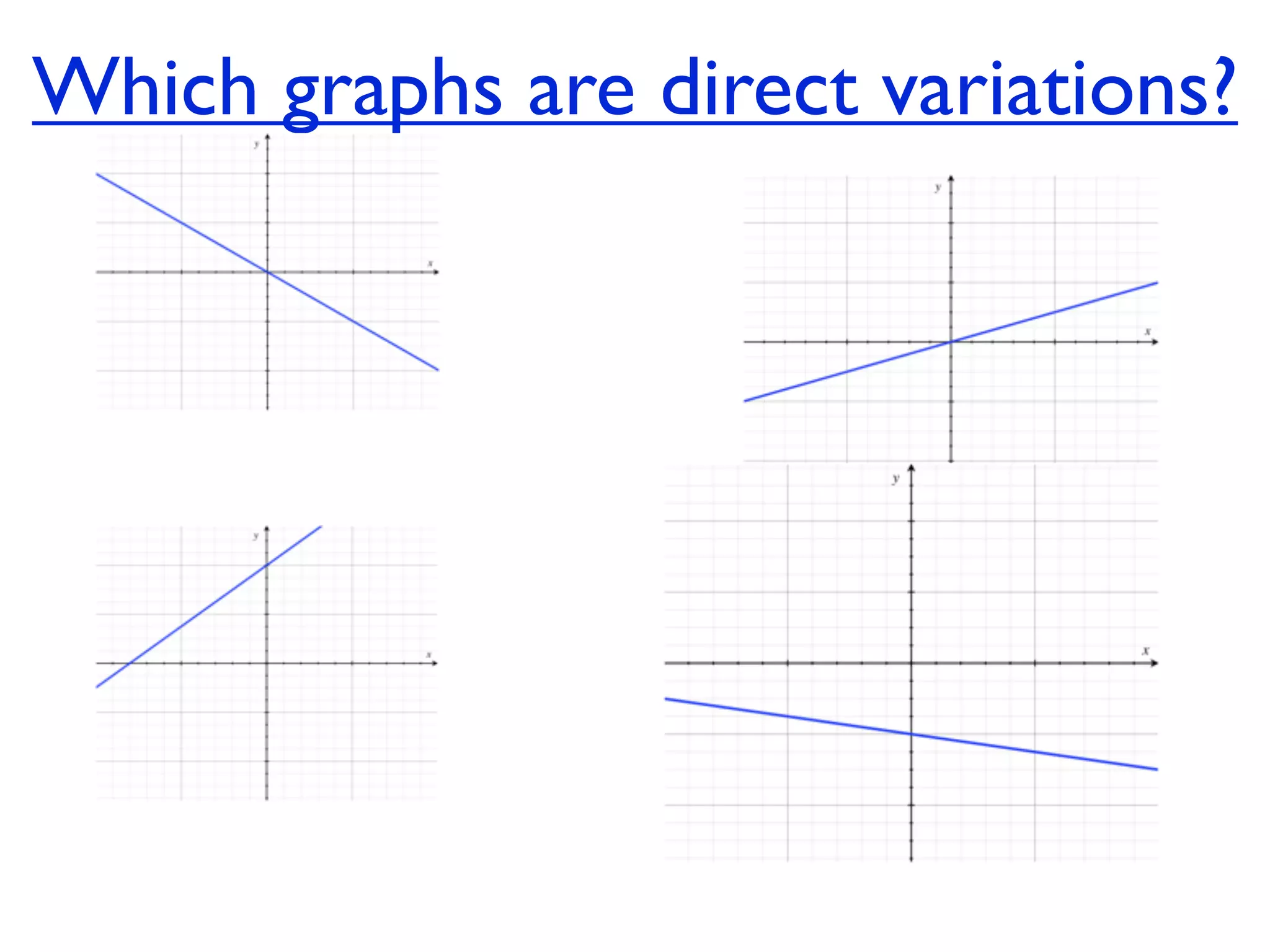
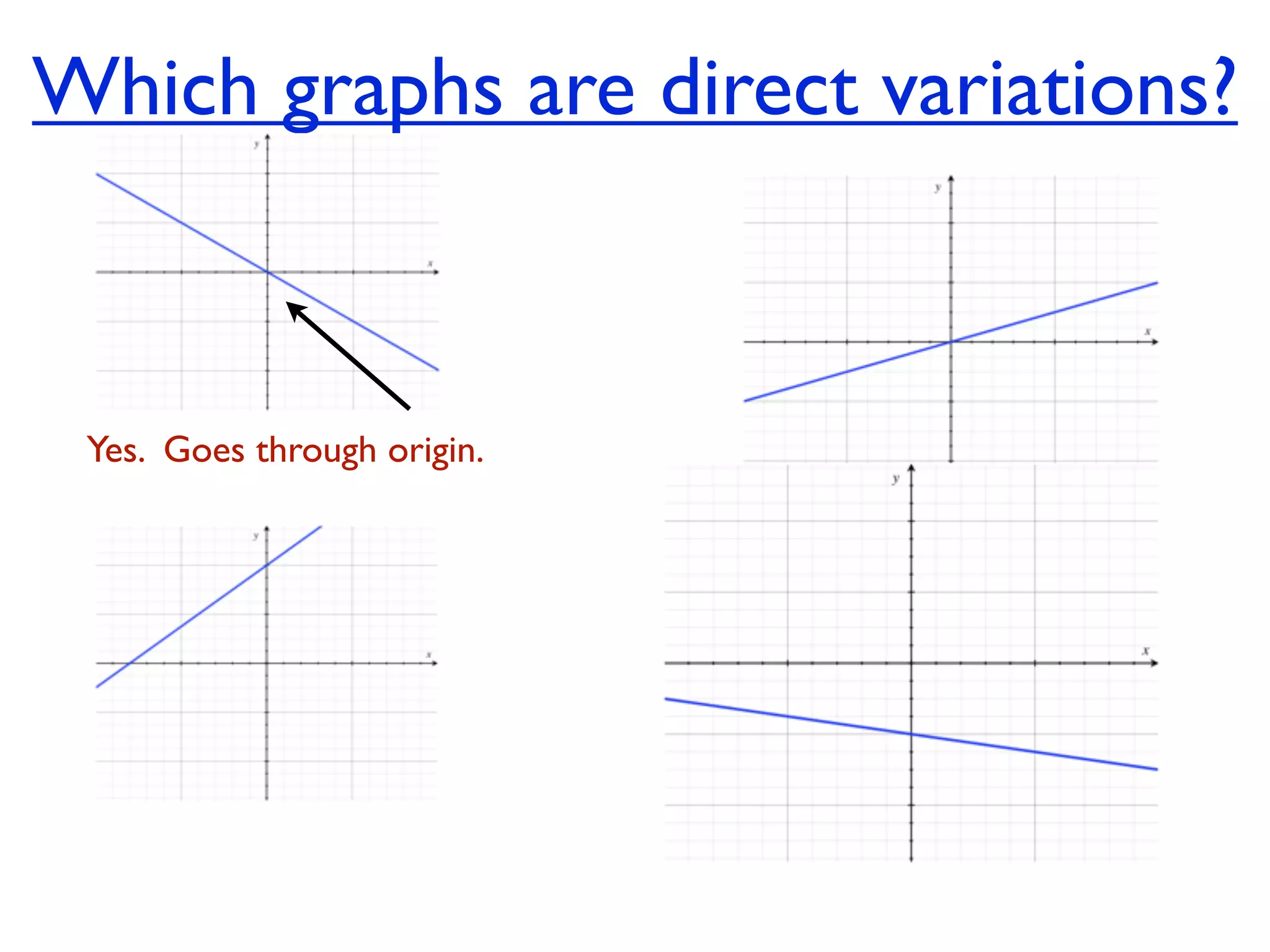
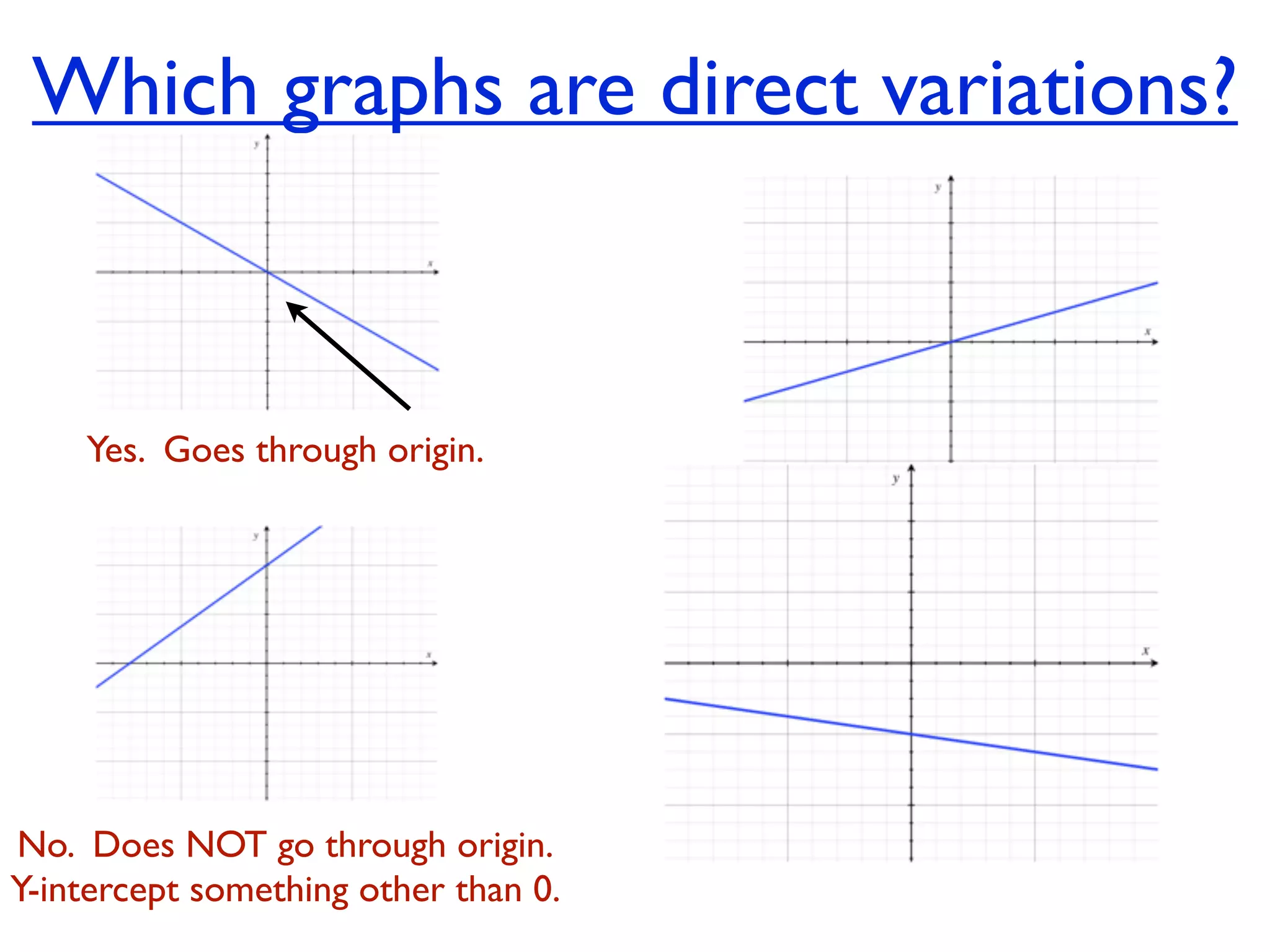
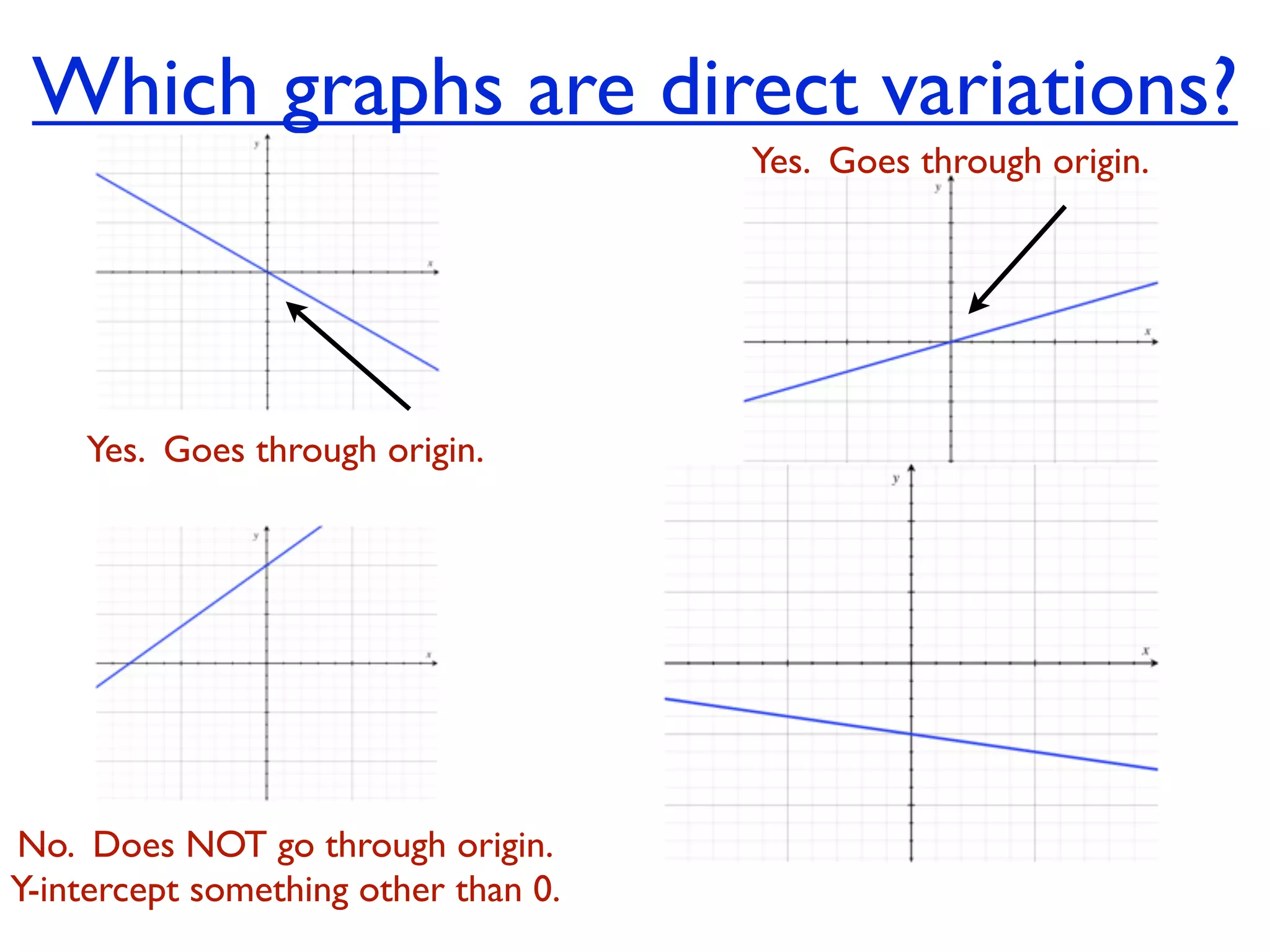
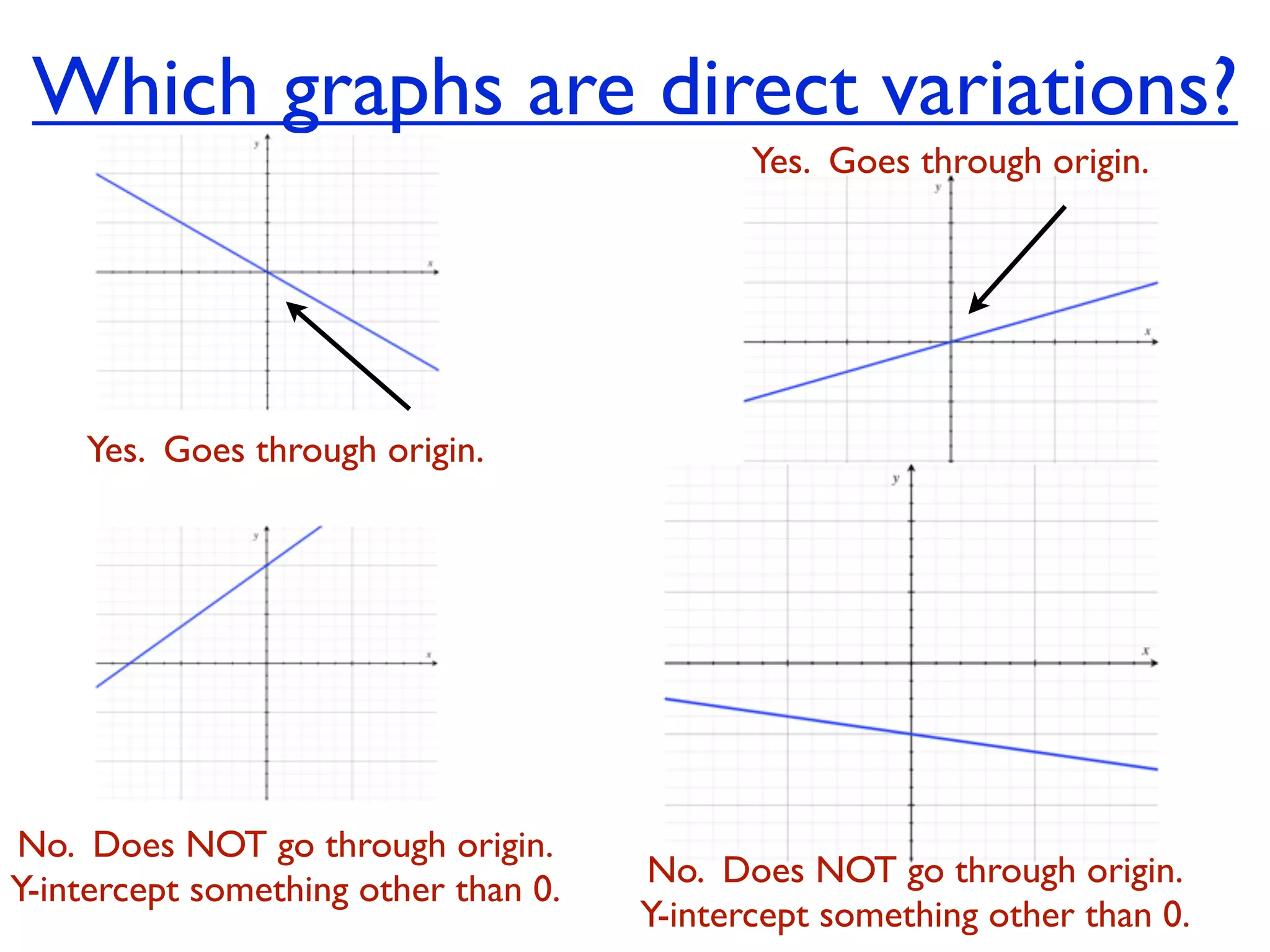
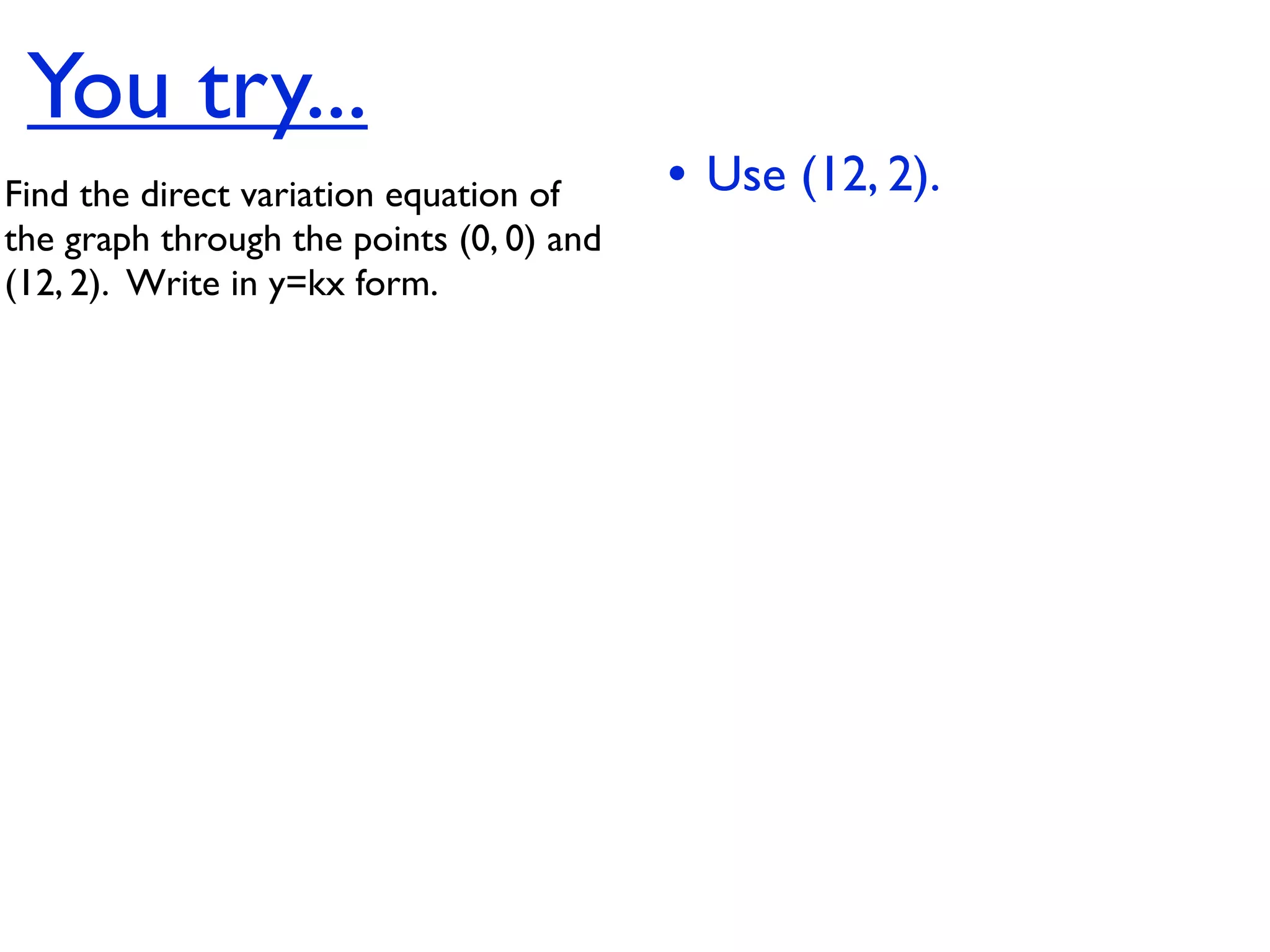
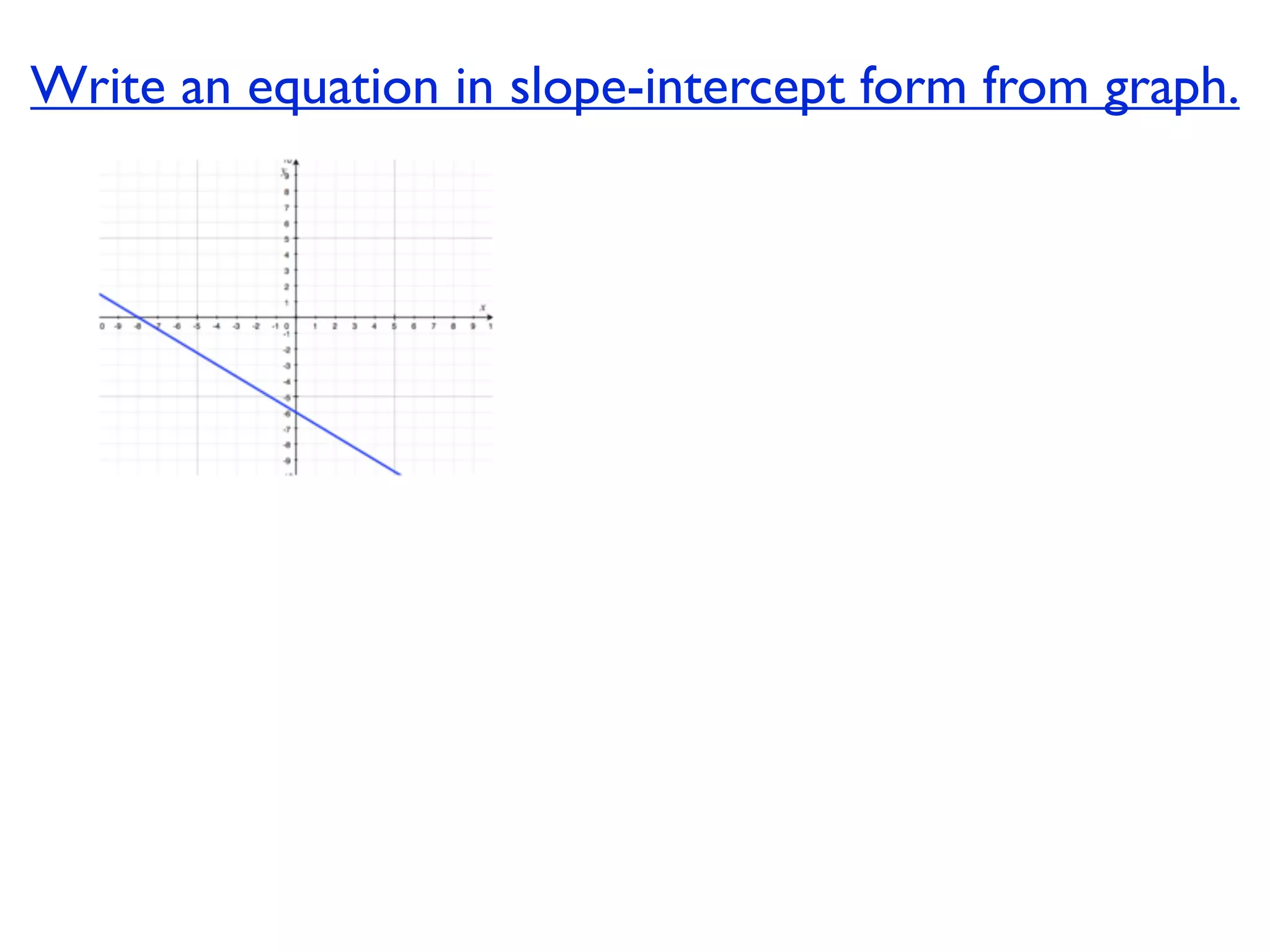
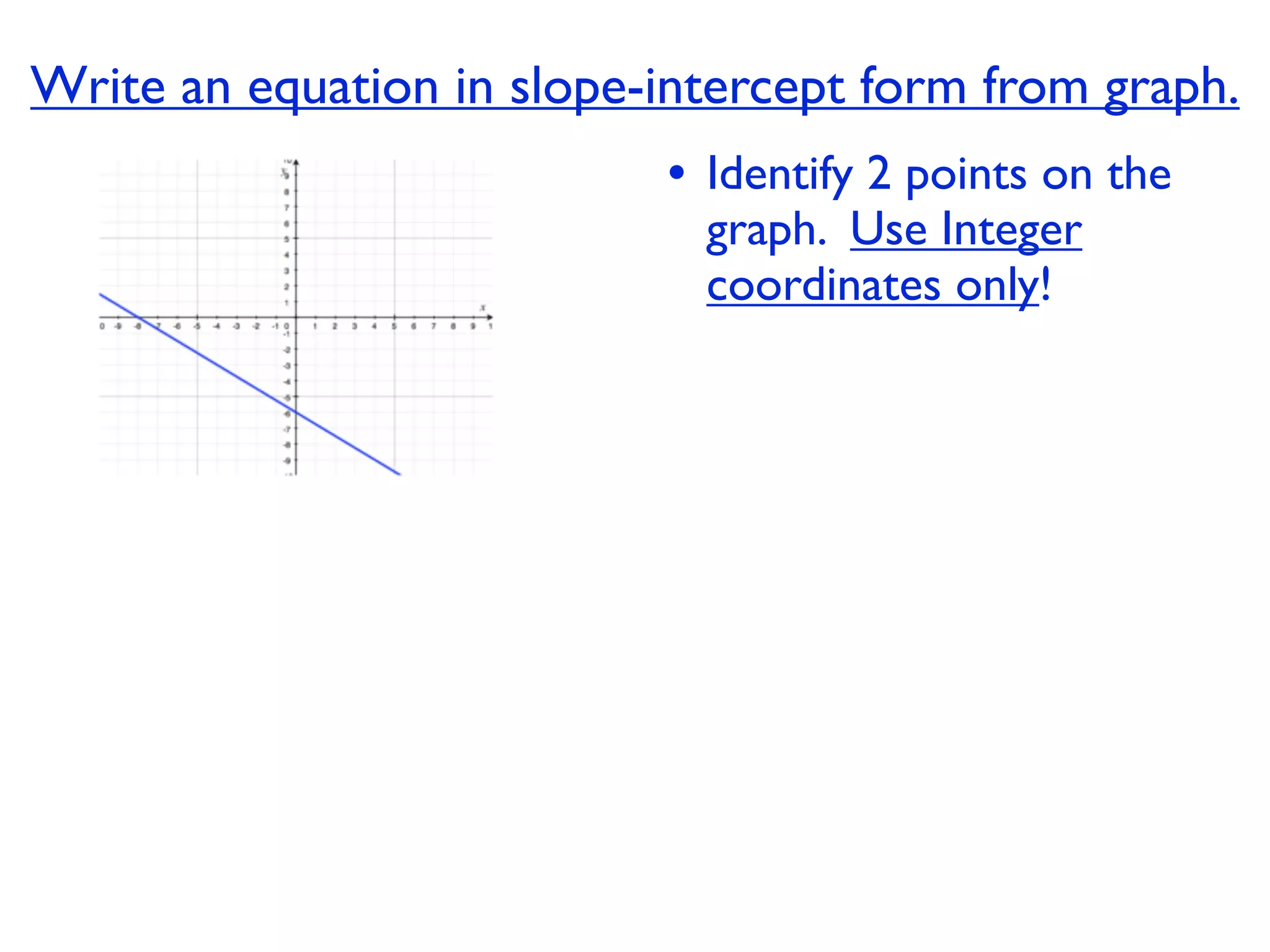
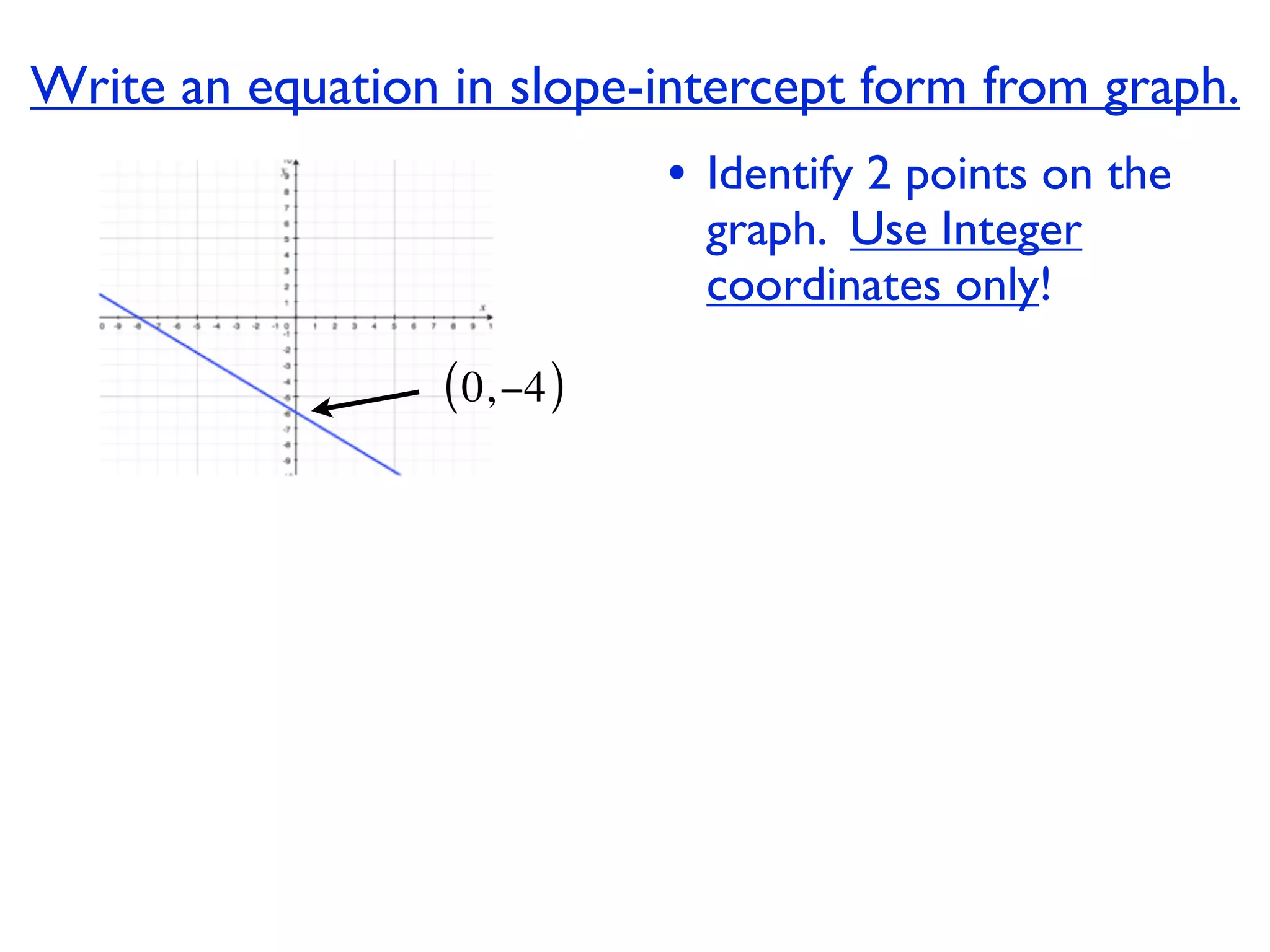
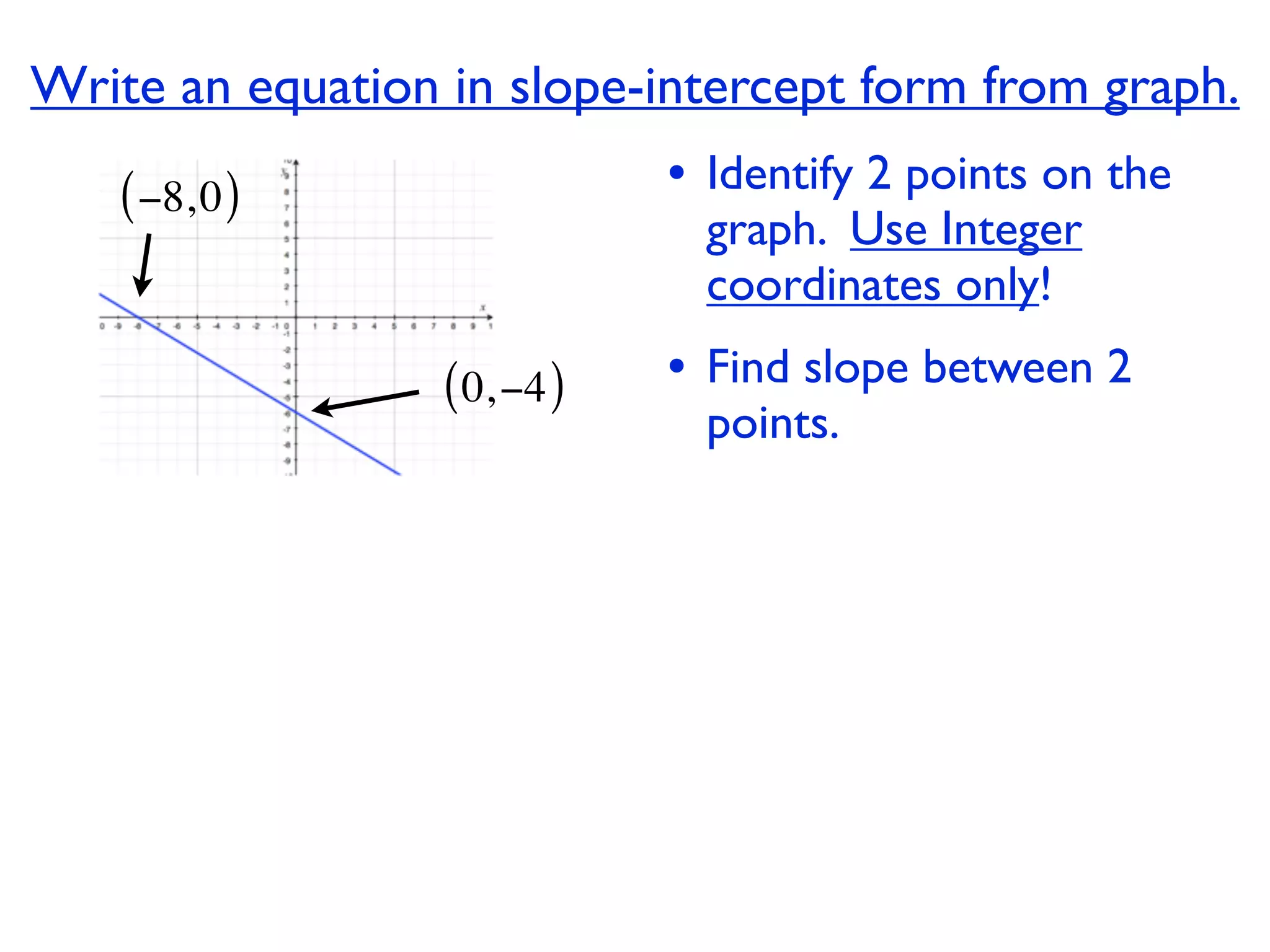
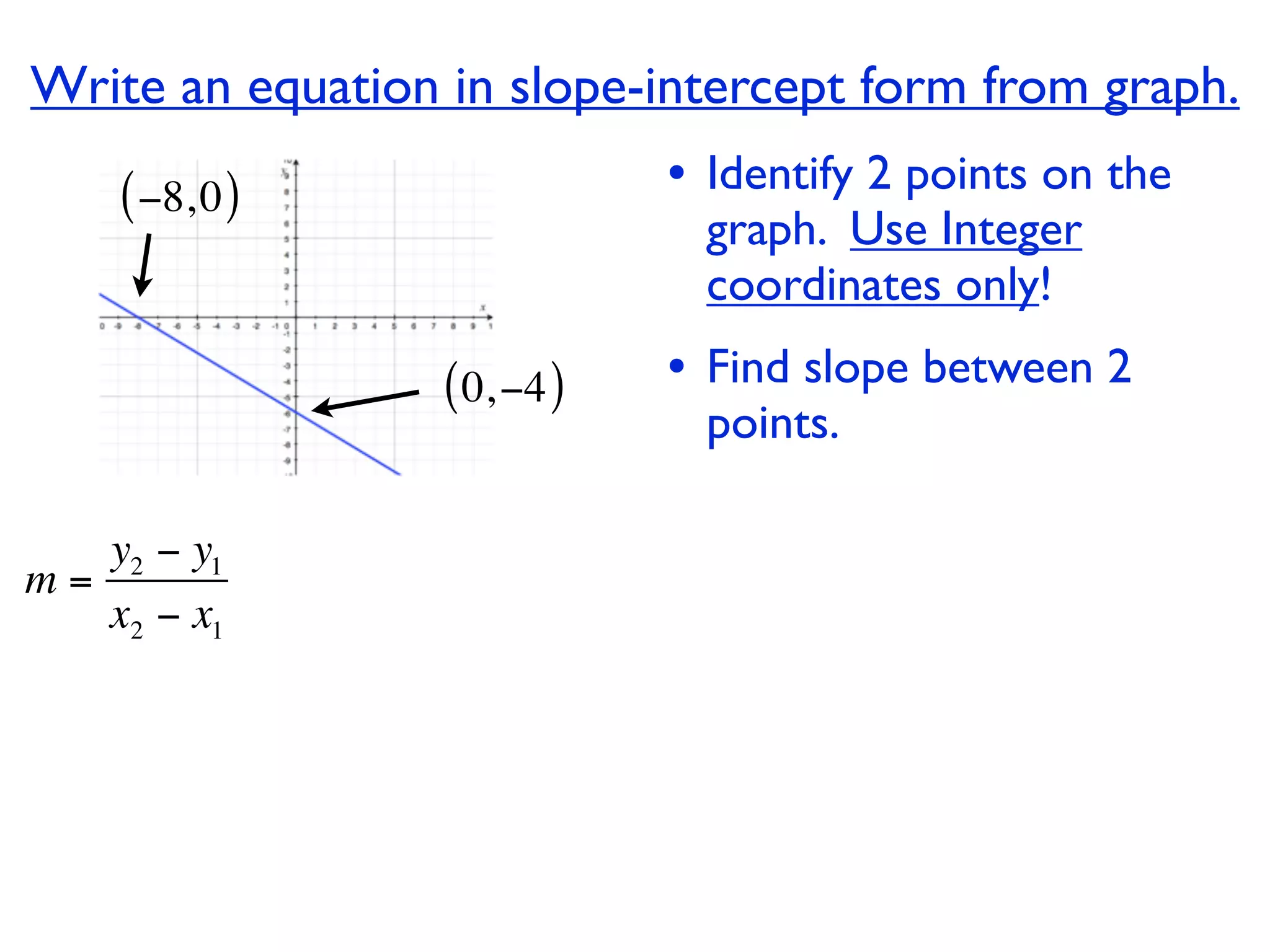
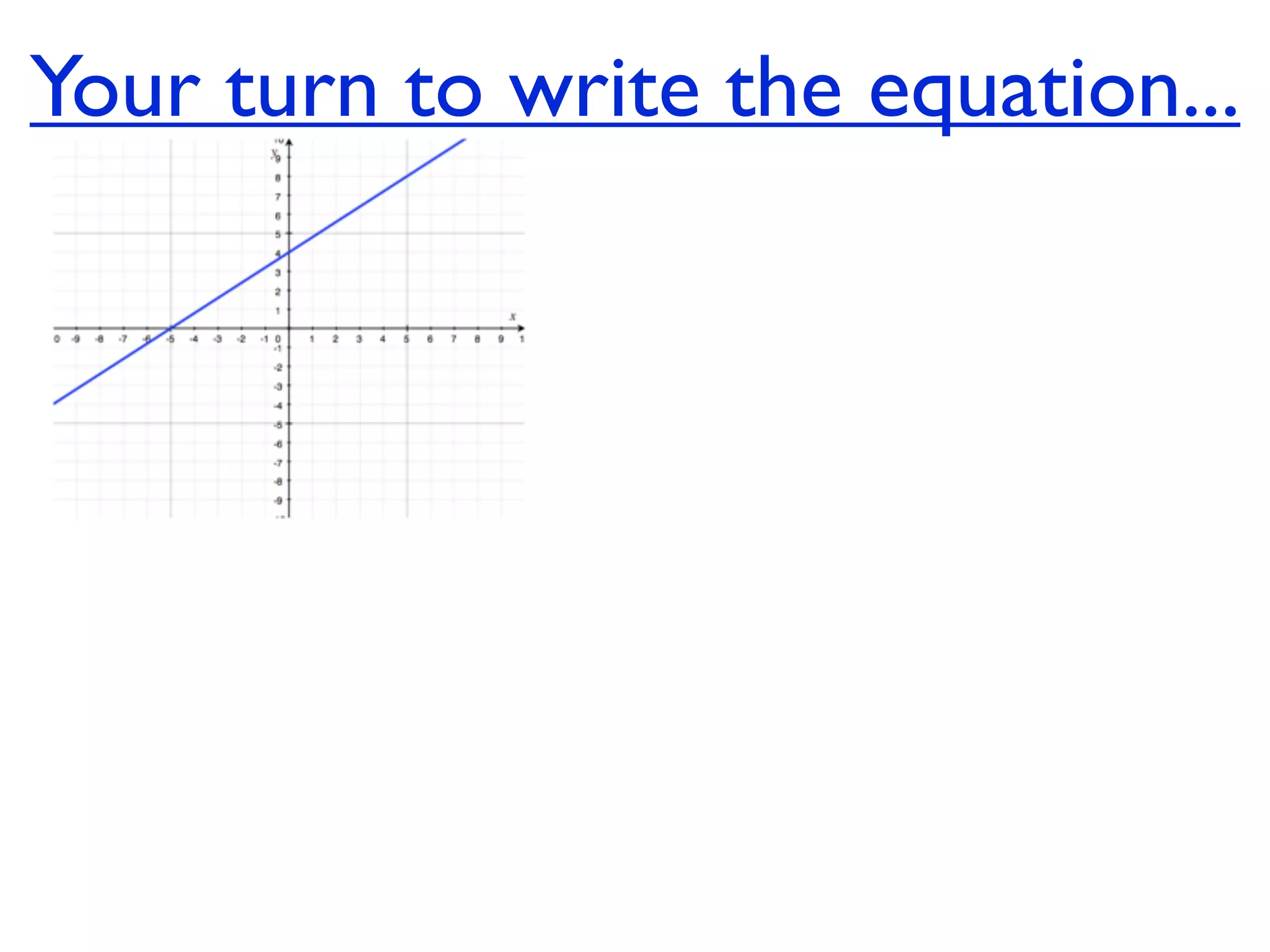
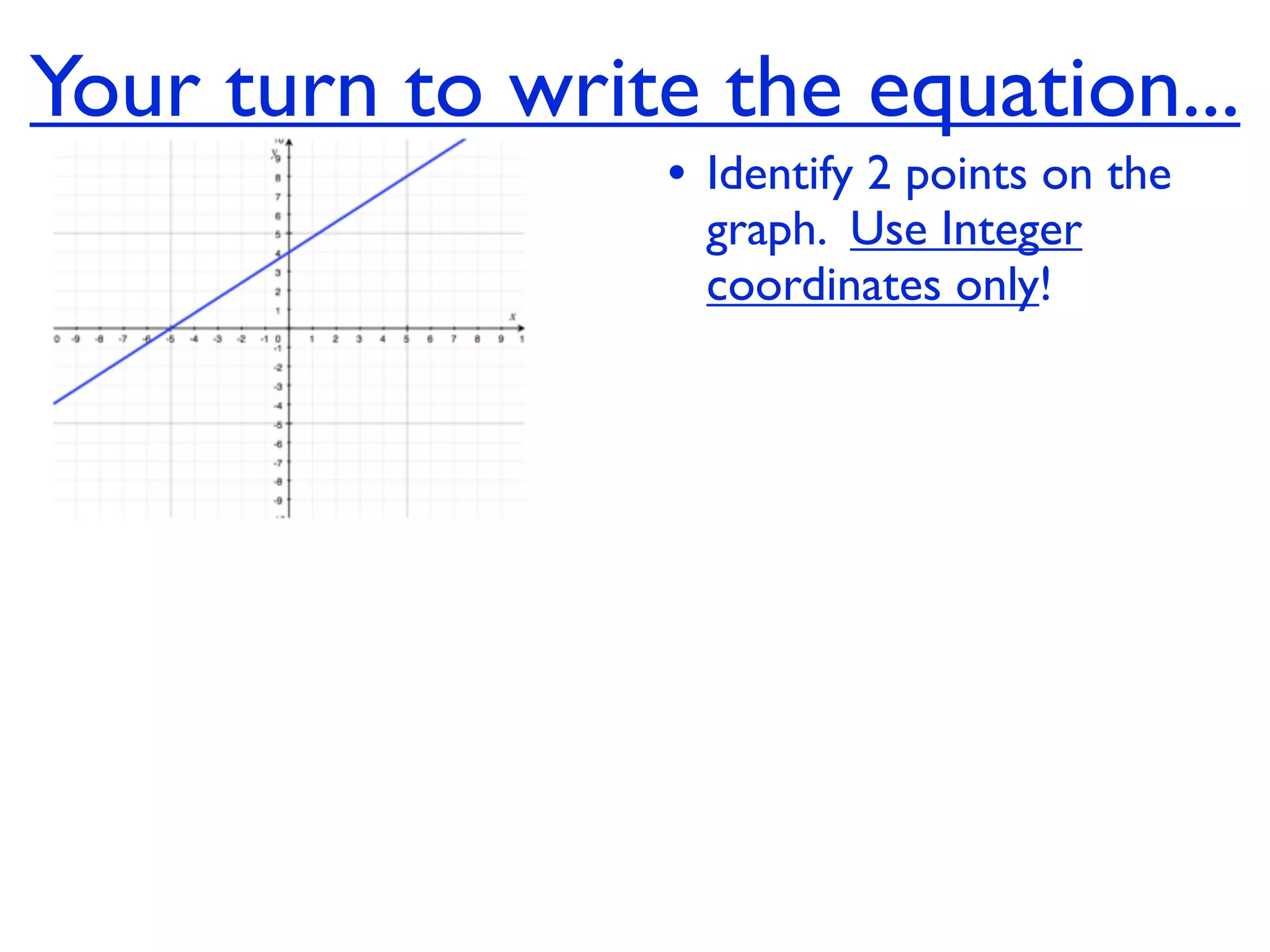
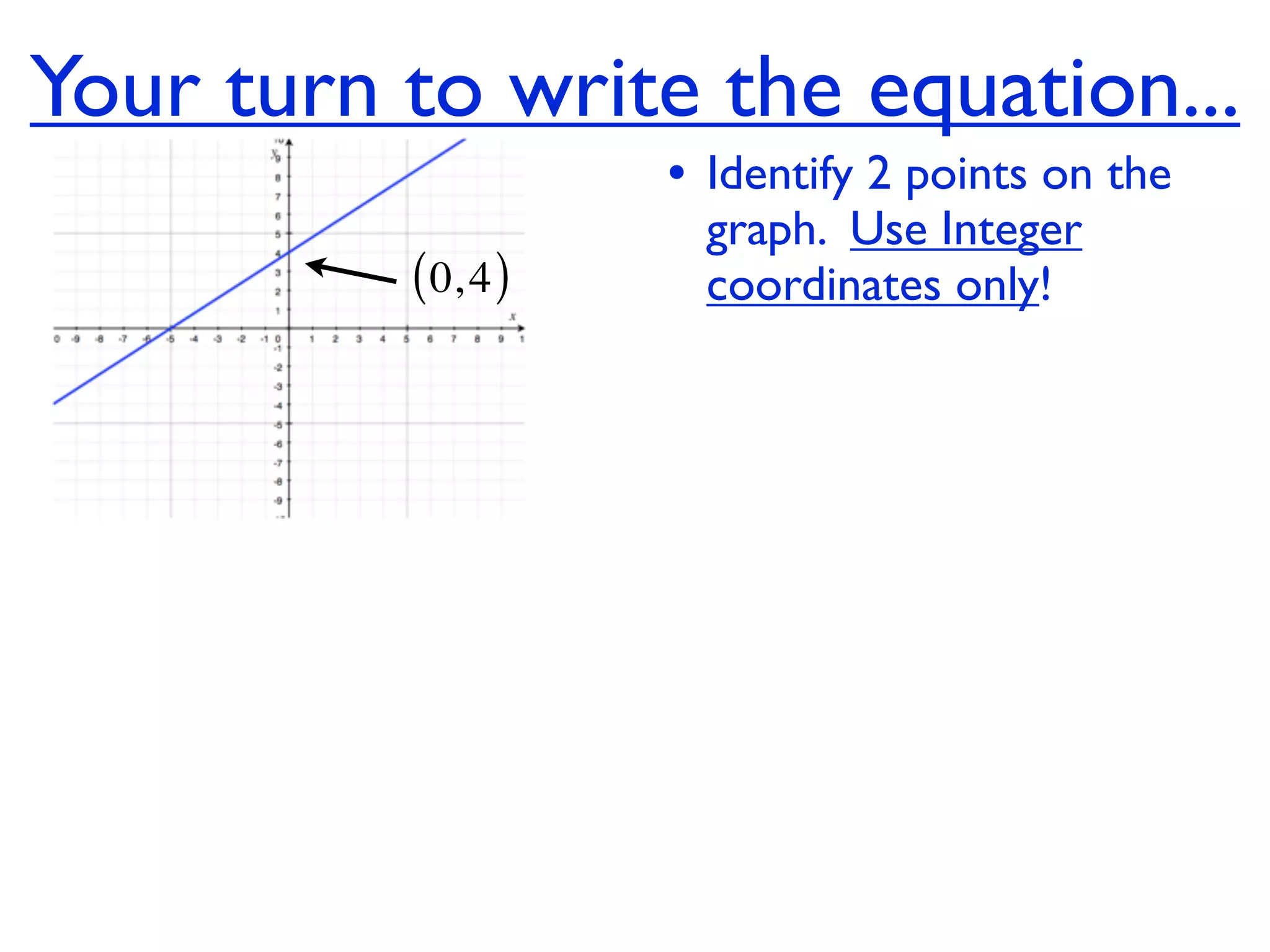
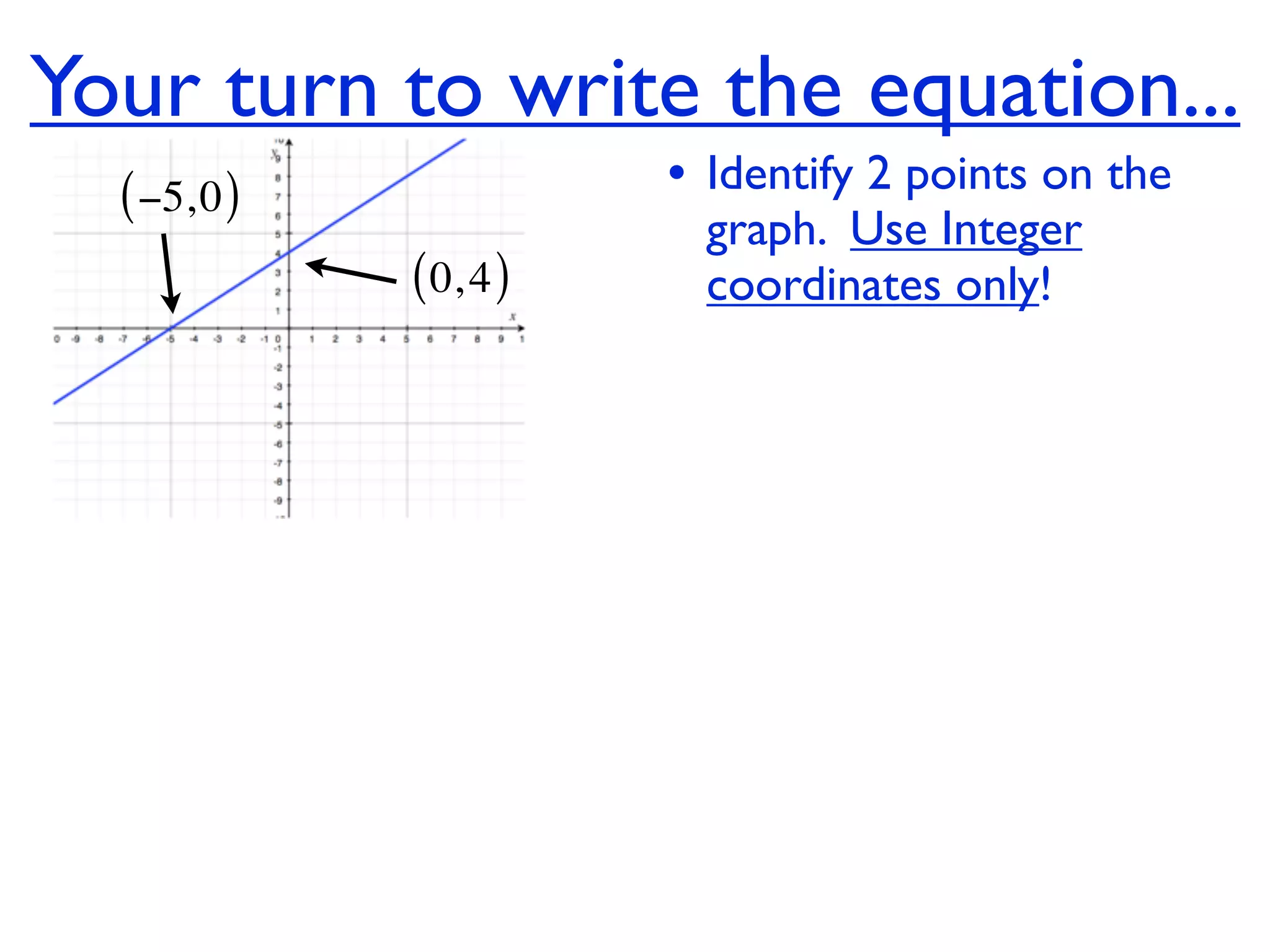
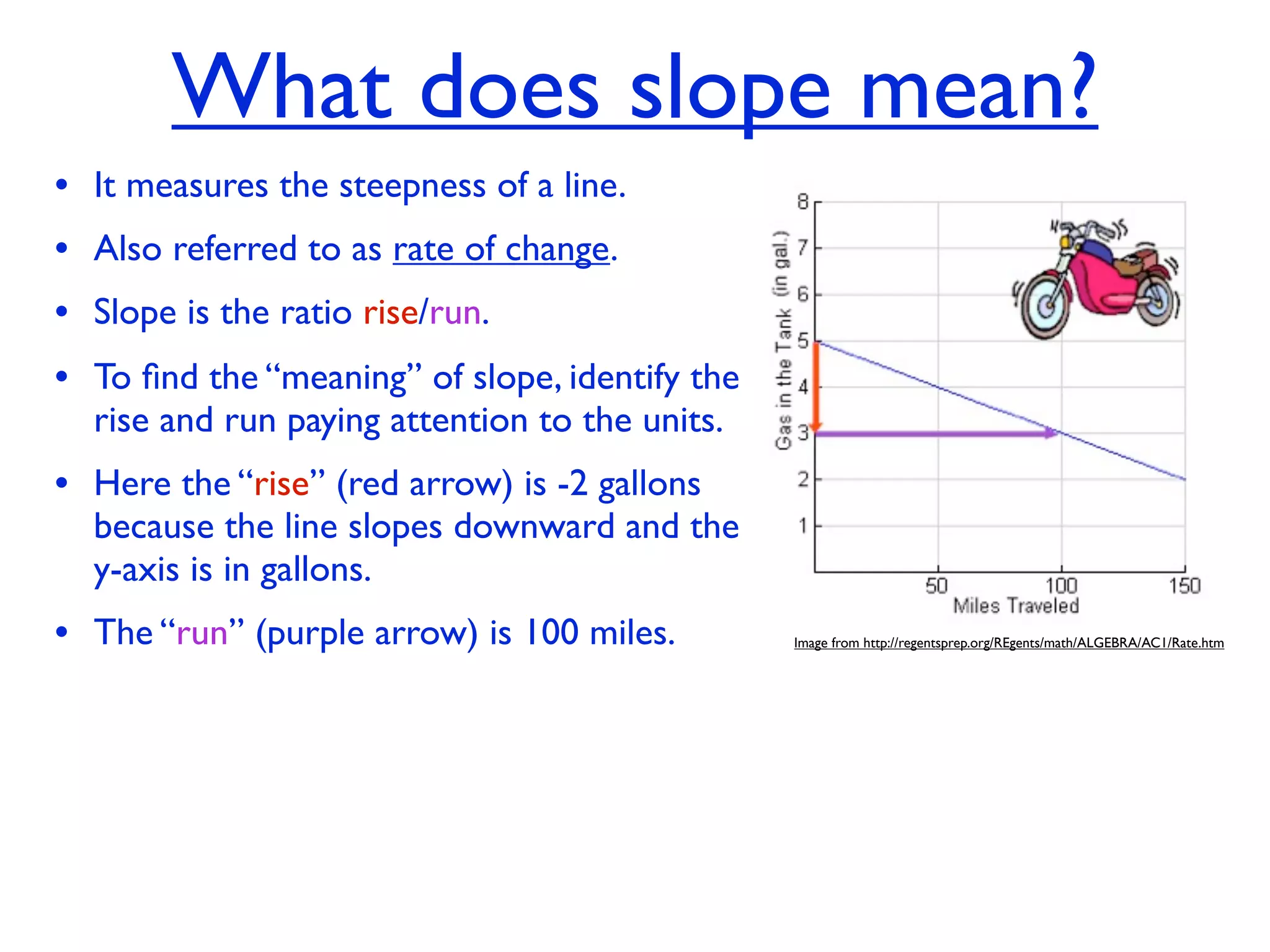
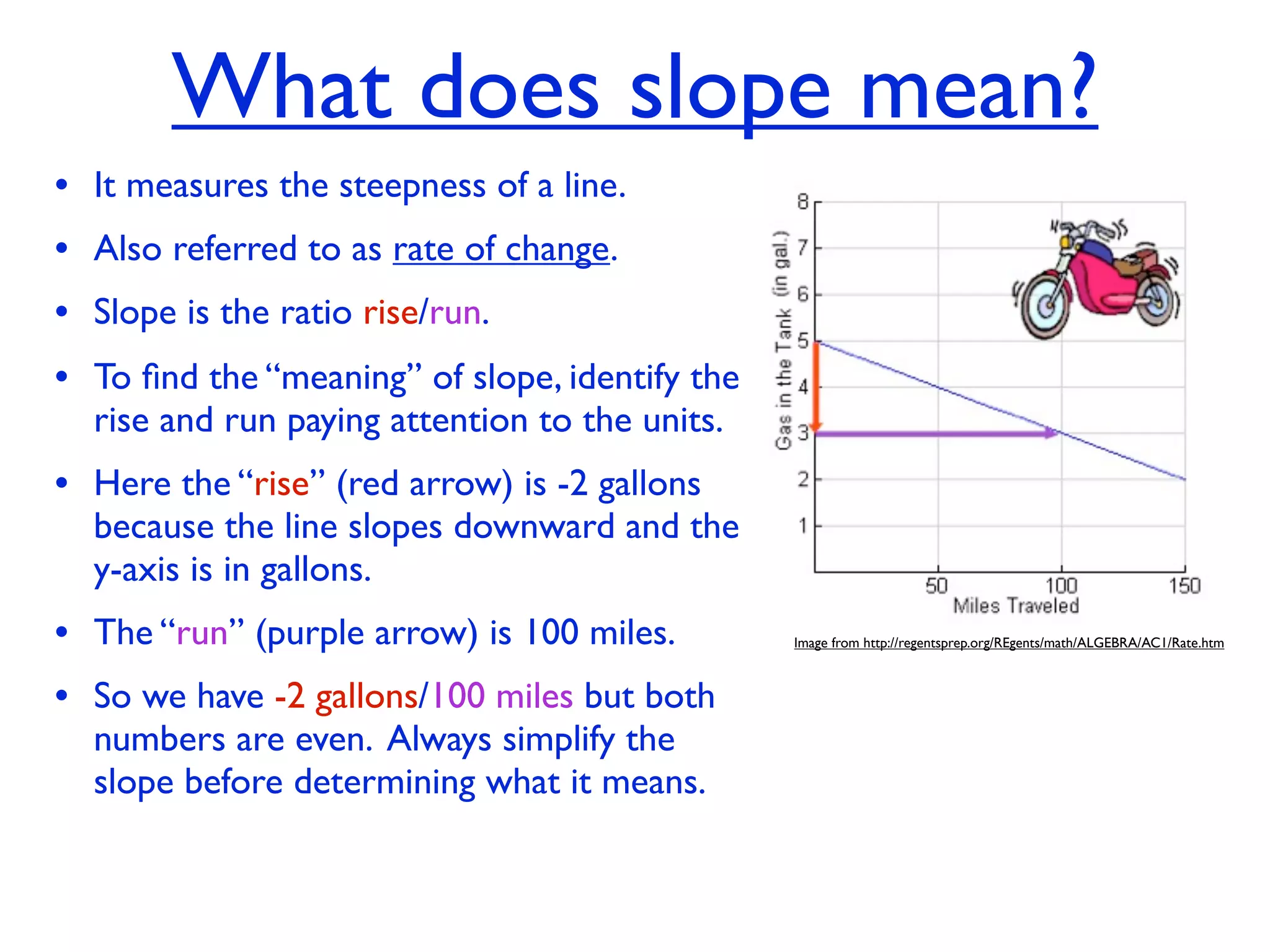
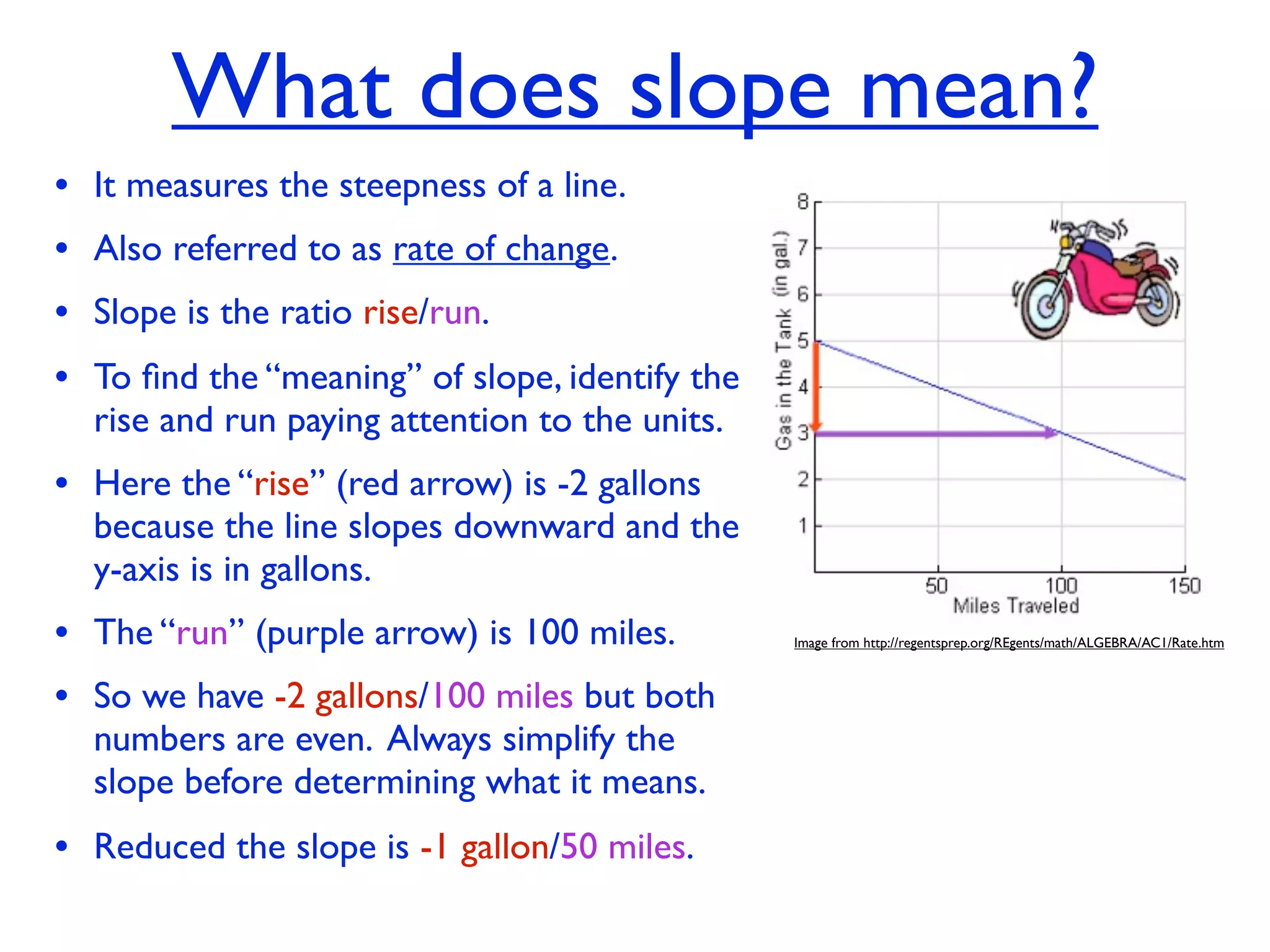
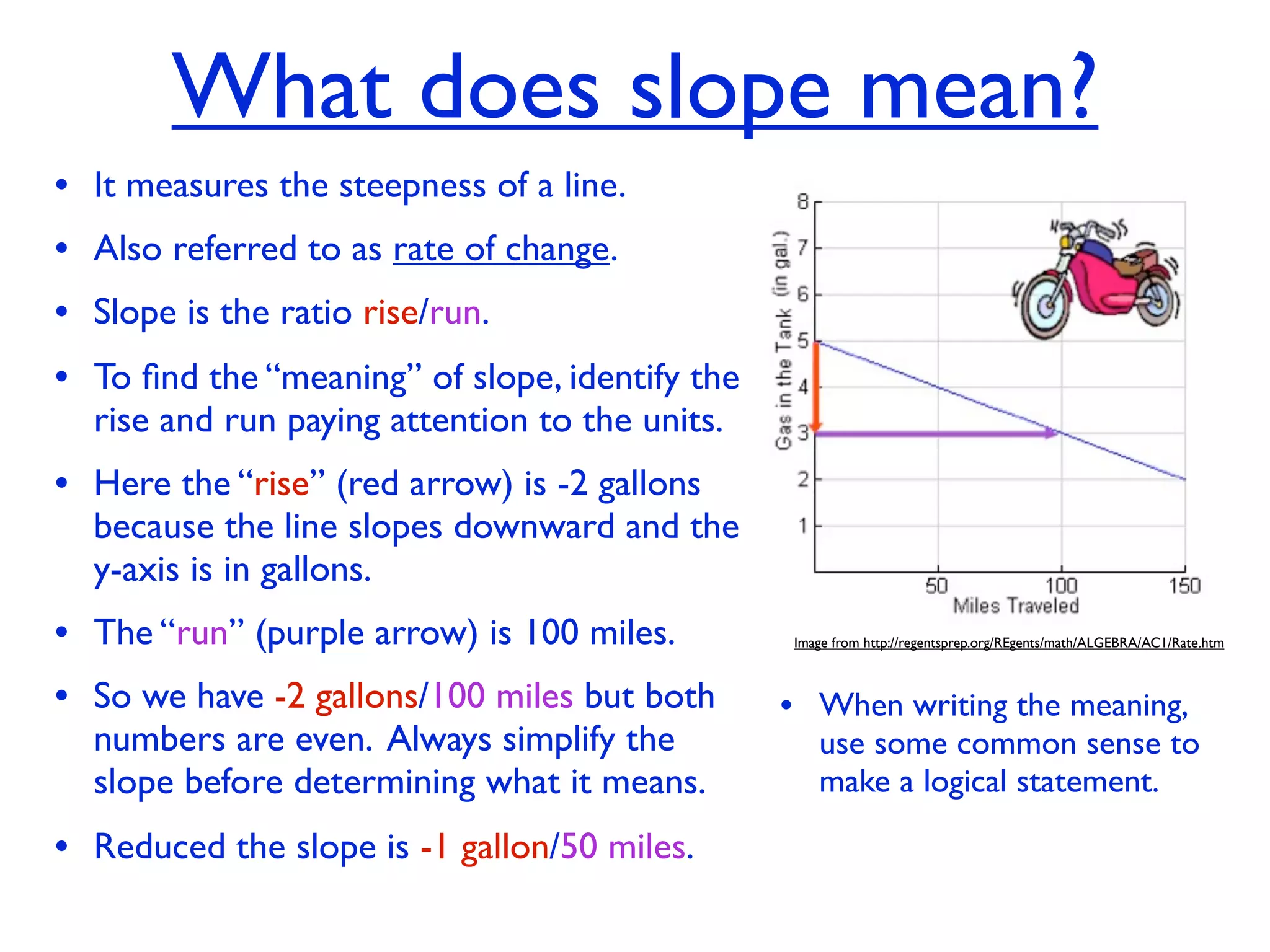
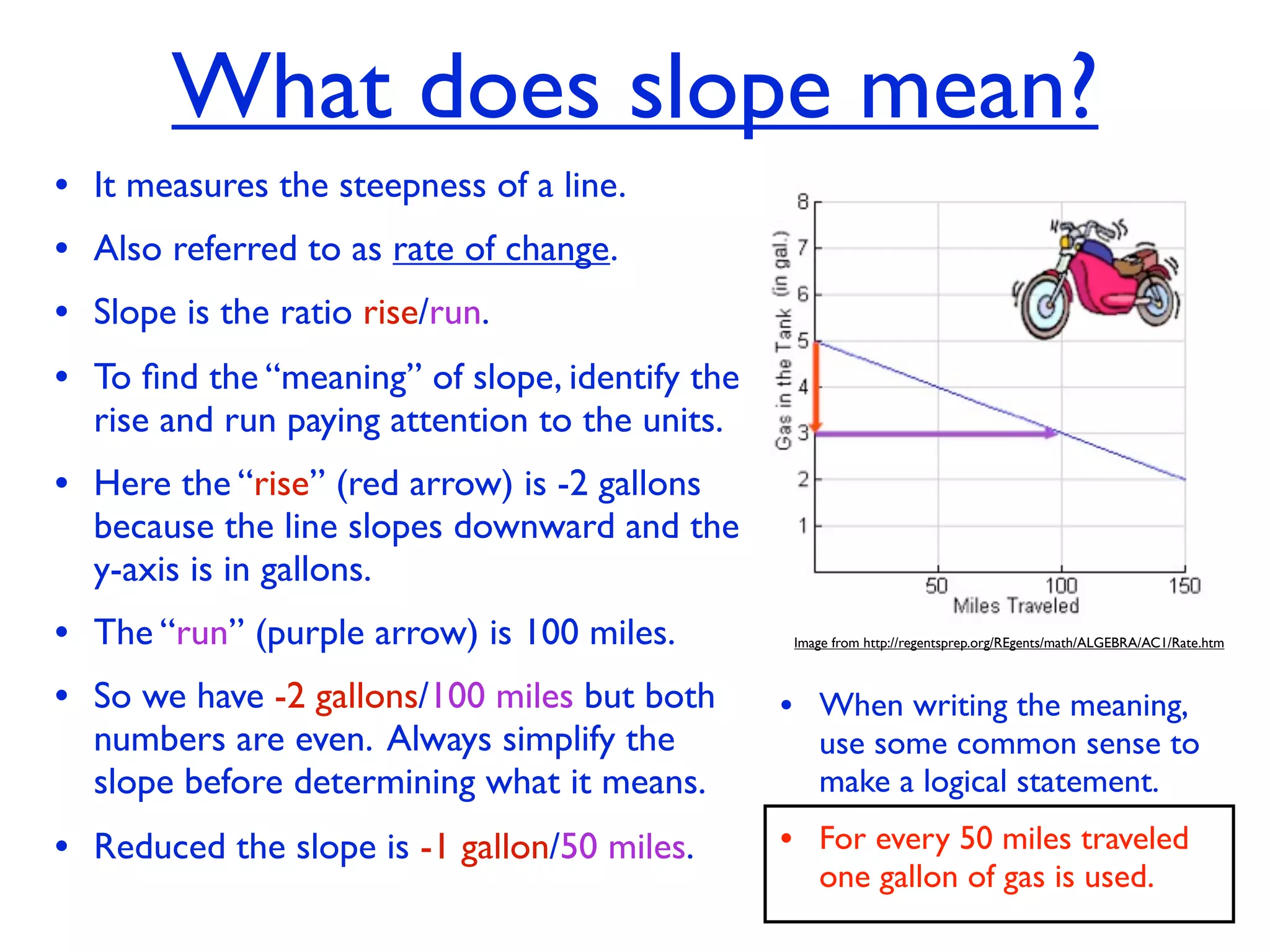
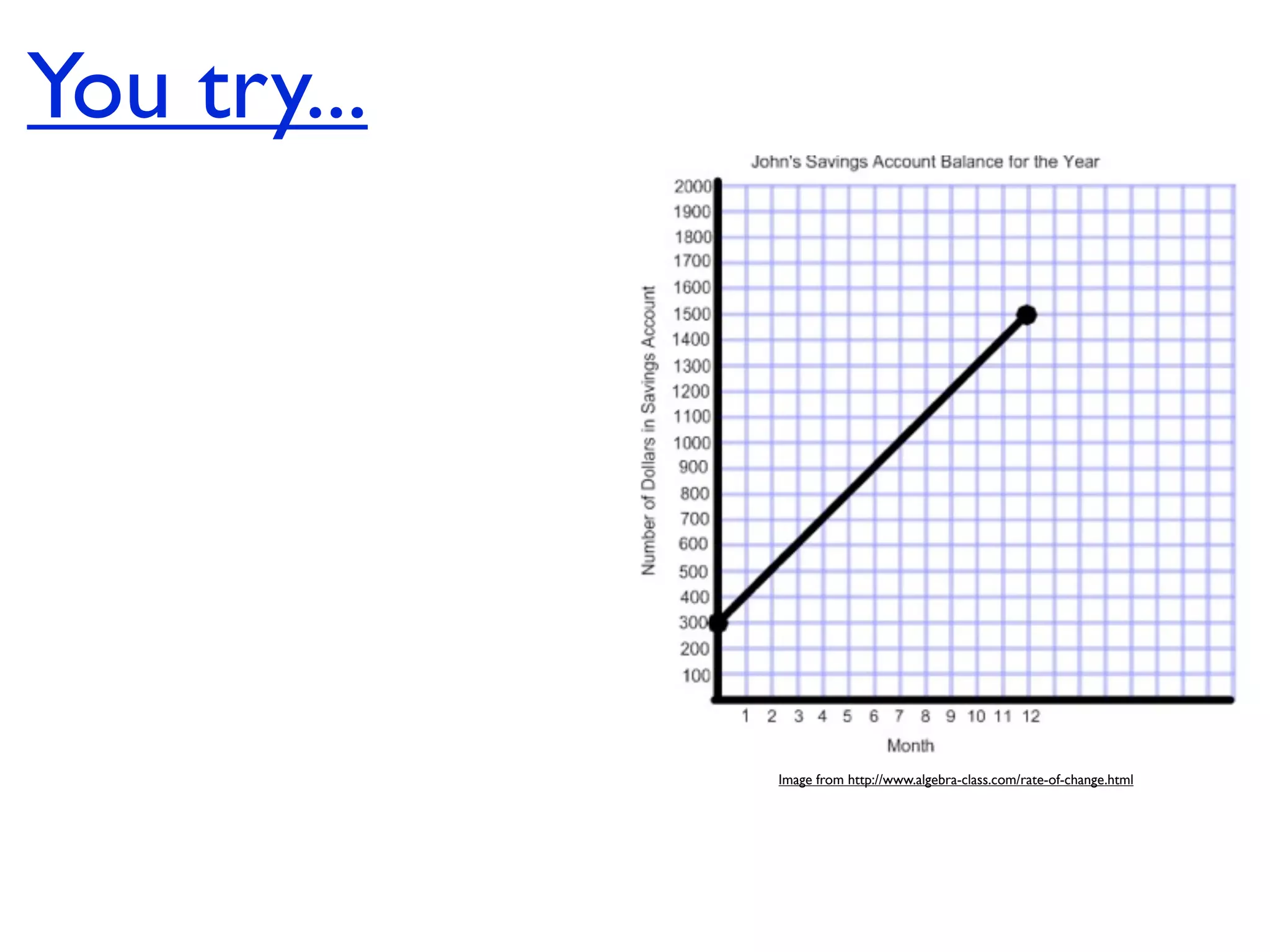
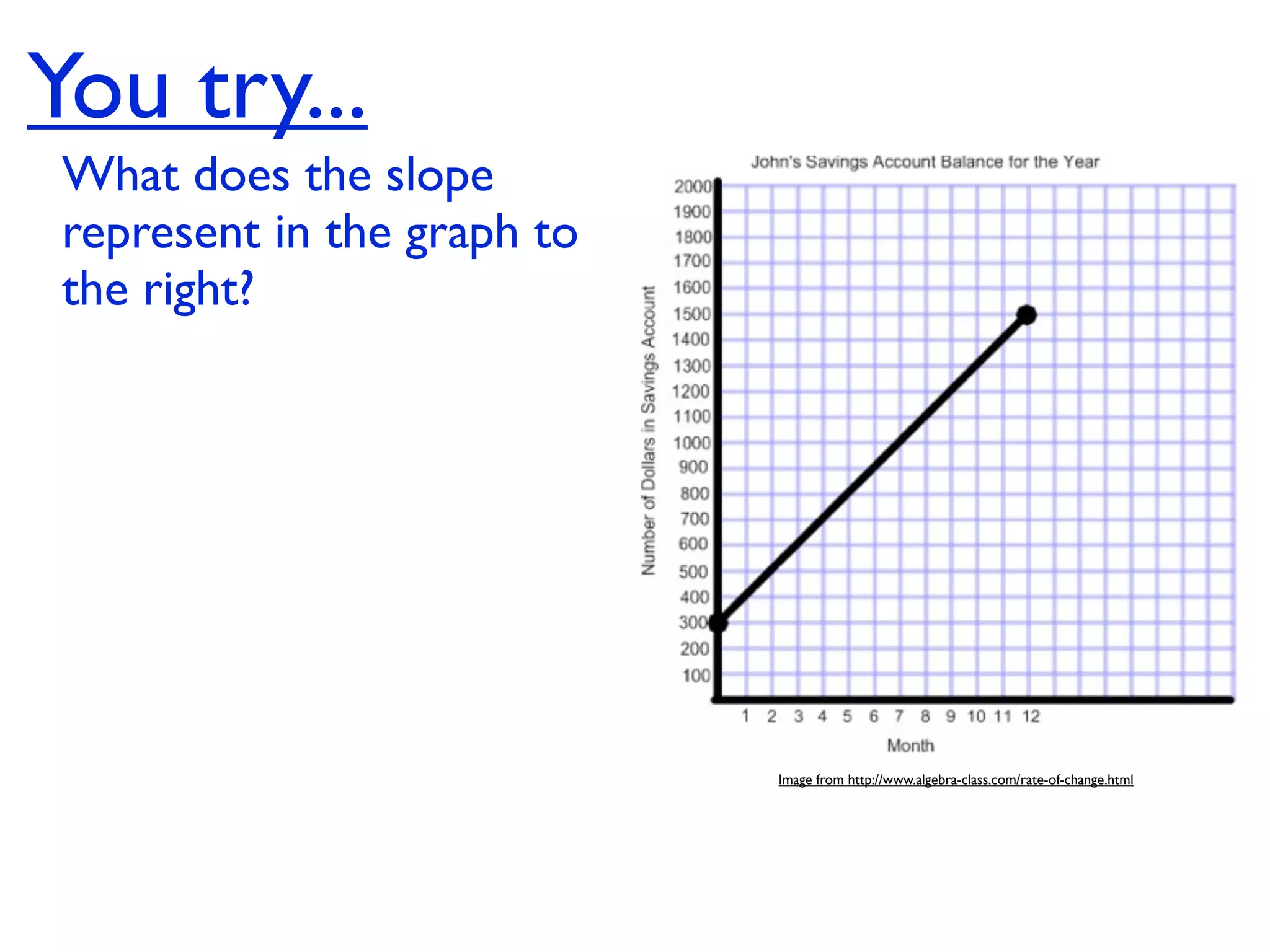
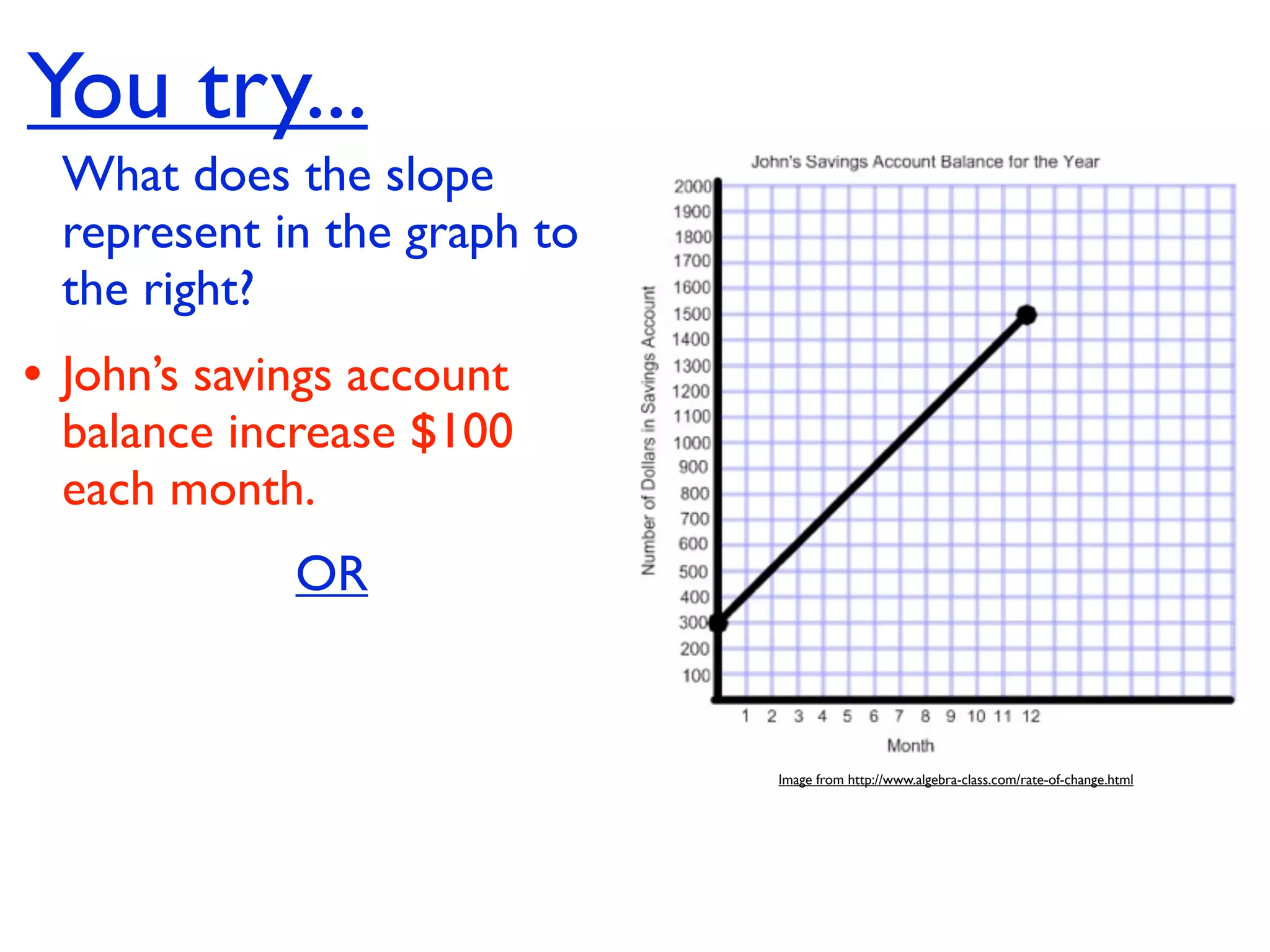
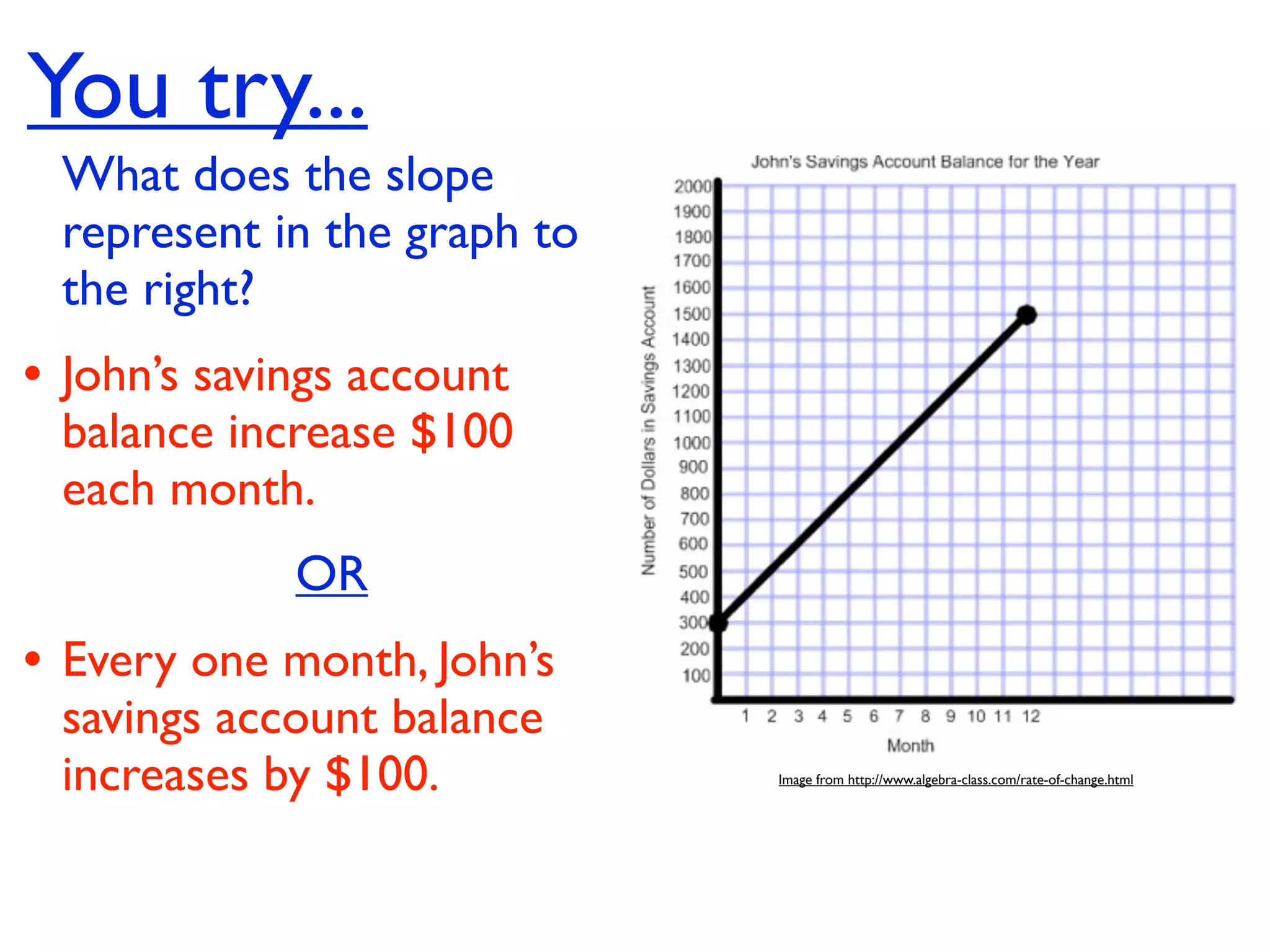
This document discusses direct variation, which is a linear equation that passes through the origin. It defines direct variation as y=kx, where k is the constant of variation. It provides examples of graphs that do and do not represent direct variations. It also shows step-by-step processes for finding the direct variation equation from two points, and for solving a direct variation problem when given a point and asked to find the corresponding y-value for a different x-value.

1. Functions
Unit 4 - Homework 7
Homework Help

2. What is direct variation?

3. What is direct variation?
• A linear equation that goes through the origin.

4. What is direct variation?
• A linear equation that goes through the origin.
• Remember a linear equation is in the form y = mx + b.

5. What is direct variation?
• A linear equation that goes through the origin.
• Remember a linear equation is in the form y = mx + b.
• A direct variation would be y = mx + 0 or just y = mx.

6. What is direct variation?
• A linear equation that goes through the origin.
• Remember a linear equation is in the form y = mx + b.
• A direct variation would be y = mx + 0 or just y = mx.
• Typically the ‘m’ is replaced with ‘k’, which stands for
constant of variation.

7. What is direct variation?
• A linear equation that goes through the origin.
• Remember a linear equation is in the form y = mx + b.
• A direct variation would be y = mx + 0 or just y = mx.
• Typically the ‘m’ is replaced with ‘k’, which stands for
constant of variation.
• General equation for direct variation is y = kx.

8. Which graphs are direct variations?

9. Which graphs are direct variations?
Yes. Goes through origin.

10. Which graphs are direct variations?
Yes. Goes through origin.
No. Does NOT go through origin.
Y-intercept something other than 0.

11. Which graphs are direct variations?
Yes. Goes through origin.
Yes. Goes through origin.
No. Does NOT go through origin.
Y-intercept something other than 0.

12. Which graphs are direct variations?
Yes. Goes through origin.
Yes. Goes through origin.
No. Does NOT go through origin.
No. Does NOT go through origin.
Y-intercept something other than 0.
Y-intercept something other than 0.

13. Steps to find Direct Variation
Find the direct variation equation of
the graph through the points (0, 0) and
(3, -5). Write in y=kx form.

14. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).

15. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
• Substitute the point into
y = kx.

16. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3

17. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3
• Solve for k.

18. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3
• Solve for k.
3 3

19. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3
• Solve for k.
3 3
5
− =k
3

20. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3
• Solve for k.
3 3
5 • Write direct variation
− =k substituting value found
3 for k in y = kx.

21. Steps to find Direct Variation
Find the direct variation equation of • Need one point other
the graph through the points (0, 0) and than (0, 0). Here we will
(3, -5). Write in y=kx form. use (3, -5).
y = kx • Substitute the point into
y = kx.
−5 = k ⋅ 3
• Solve for k.
3 3
5 • Write direct variation
− =k substituting value found
3 for k in y = kx.
5
y=− x
3

22. You try...
Find the direct variation equation of
the graph through the points (0, 0) and
(12, 2). Write in y=kx form.

23. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form.

24. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.

25. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx
2 = k ⋅12

26. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx • Solve for k.
2 = k ⋅12

27. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx • Solve for k.
2 = k ⋅12
12 12

28. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx • Solve for k.
2 = k ⋅12
12 12
1
=k
6

29. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx • Solve for k.
2 = k ⋅12 • Write direct variation
12 12 substituting value found
for k into y = kx.
1
=k
6

30. You try...
Find the direct variation equation of • Use (12, 2).
the graph through the points (0, 0) and
(12, 2). Write in y=kx form. • Substitute the point into
y = kx.
y = kx • Solve for k.
2 = k ⋅12 • Write direct variation
12 12 substituting value found
for k into y = kx.
1
=k
6 1
y= x
6

31. Find Direct Variation w/o point
Write a direct variation equation that
relates x to y. Then solve. Show both
the equation and the solution. If
y = 15 when x = 3, find y when x = 4.

32. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.

33. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.

34. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
• Substitute the “if...when”
values into y = kx.

35. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3

36. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.

37. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3

38. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3
5=k

39. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.

40. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x

41. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x • Now use the “find...when” by
substituting the given value.

42. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x • Now use the “find...when” by
substituting the given value.
• In this case we are given x=4.

43. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x • Now use the “find...when” by
substituting the given value.
y = 5⋅4 • In this case we are given x=4.

44. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x • Now use the “find...when” by
substituting the given value.
y = 5⋅4 • In this case we are given x=4.
• Simplify to find y.

45. Find Direct Variation w/o point
Write a direct variation equation that • The “if..when” has the pieces
relates x to y. Then solve. Show both found in an ordered pair. Use
the equation and the solution. If these values to find k.
y = 15 when x = 3, find y when x = 4.
y = kx • Substitute the “if...when”
values into y = kx.
15 = k ⋅ 3 • Solve for k.
3 3 • Write direct variation
5=k substituting value found for k.
y = 5x • Now use the “find...when” by
substituting the given value.
y = 5⋅4 • In this case we are given x=4.
y = 20 • Simplify to find y.

46. Your turn...
Write a direct variation equation that
relates x to y. Then solve. Show both
the equation and the solution. If
y = 21 when x = 7, find y when x = 6.

47. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6.

48. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6.

49. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
values into y = kx.

50. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
21 = k ⋅ 7

51. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7

52. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
7 7

53. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
7 7
3= k

54. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k

55. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
y = 3x

56. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
• Now use the “find...when” by
y = 3x substituting the given value.

57. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
• Now use the “find...when” by
y = 3x substituting the given value.
• In this case we are given x=6.

58. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
• Now use the “find...when” by
y = 3x substituting the given value.
y = 3⋅ 6 • In this case we are given x=6.

59. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
• Now use the “find...when” by
y = 3x substituting the given value.
y = 3⋅ 6 • In this case we are given x=6.
• Simplify to find y.

60. Your turn...
Write a direct variation equation that • Identify “if..when” values to
relates x to y. Then solve. Show both find k.
the equation and the solution. If
y = 21 when x = 7, find y when x = 6. • Substitute the “if...when”
y = kx values into y = kx.
• Solve for k.
21 = k ⋅ 7
• Write direct variation
7 7 substituting value found for k.
3= k
• Now use the “find...when” by
y = 3x substituting the given value.
y = 3⋅ 6 • In this case we are given x=6.
y = 18 • Simplify to find y.

61. Write an equation in slope-intercept form from graph.

62. Write an equation in slope-intercept form from graph.
• Identify 2 points on the
graph. Use Integer
coordinates only!

63. Write an equation in slope-intercept form from graph.
• Identify 2 points on the
graph. Use Integer
coordinates only!
( 0, −4 )

64. Write an equation in slope-intercept form from graph.
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( 0, −4 )

65. Write an equation in slope-intercept form from graph.
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( 0, −4 ) • Find slope between 2
points.

66. Write an equation in slope-intercept form from graph.
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( 0, −4 ) • Find slope between 2
points.
y2 − y1
m=
x2 − x1

67. Write an equation in slope-intercept form from graph.
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1

68. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1

69. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1 • Substitute.

70. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0
m= =
x2 − x1 0 − ( −8 ) • Substitute.

71. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0
m= =
x2 − x1 0 − ( −8 ) • Substitute.
• Simplify.

72. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0 −4 −1
m= = =
x2 − x1 0 − ( −8 ) 8
=
2 • Substitute.
• Simplify.

73. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0 −4 −1
m= = =
x2 − x1 0 − ( −8 ) 8
=
2 • Substitute.
• Simplify.
• Use the slope and y-
intercept to write
equation.

74. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0 −4 −1
m= = =
x2 − x1 0 − ( −8 ) 8
=
2 • Substitute.
• Simplify.
y = mx + b • Use the slope and y-
intercept to write
equation.

75. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0 −4 −1
m= = =
x2 − x1 0 − ( −8 ) 8
=
2 • Substitute.
• Simplify.
y = mx + b • Use the slope and y-
intercept to write
equation.

76. Write an equation in slope-intercept form from graph.
( x1, y1 )
( −8, 0 ) • Identify 2 points on the
graph. Use Integer
coordinates only!
( x2 , y2 )
( 0, −4 ) • Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 −4 − 0 −4 −1
m= = =
x2 − x1 0 − ( −8 ) 8
=
2 • Substitute.
• Simplify.
y = mx + b • Use the slope and y-
1 intercept to write
y=− x−4 equation.
2

77. Your turn to write the equation...

78. Your turn to write the equation...
• Identify 2 points on the
graph. Use Integer
coordinates only!

79. Your turn to write the equation...
• Identify 2 points on the
graph. Use Integer
( 0, 4 ) coordinates only!

80. Your turn to write the equation...
( −5, 0 ) • Identify 2 points on the
graph. Use Integer
( 0, 4 ) coordinates only!

81. Your turn to write the equation...
( −5, 0 ) • Identify 2 points on the
graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.

82. Your turn to write the equation...
( −5, 0 ) • Identify 2 points on the
graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
y2 − y1
m=
x2 − x1

83. Your turn to write the equation...
( −5, 0 ) • Identify 2 points on the
graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1

84. Youry )turn to write the equation...
(x ,1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1

85. Youry )turn to write the equation...
(x ,1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1
m=
x2 − x1 • Substitute.

86. Youry )turn to write the equation...
(x , 1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 4−0
m= =
x2 − x1 0 − ( −5 ) • Substitute.

87. Youry )turn to write the equation...
(x , 1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 4−0
m= =
x2 − x1 0 − ( −5 ) • Substitute.
• Simplify.

88. Youry )turn to write the equation...
(x ,1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 4−0 4
m= = =
x2 − x1 0 − ( −5 ) 5 • Substitute.
• Simplify.

89. Youry )turn to write the equation...
(x ,1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 4−0 4
m= = =
x2 − x1 0 − ( −5 ) 5 • Substitute.
• Simplify.
• Use the slope and y-
intercept to write
equation.

90. Youry )turn to write the equation...
(x ,1 1
( −5, 0 ) • Identify 2 points on the
( x2 , y2 ) graph. Use Integer
( 0, 4 ) coordinates only!
• Find slope between 2
points.
• Label points as 1’s and 2’s.
y2 − y1 4−0 4
m= = =
x2 − x1 0 − ( −5 ) 5 • Substitute.
• Simplify.
y = mx + b • Use the slope and y-
4 intercept to write
y= x+4 equation.
5

91. A couple comments about
picking points on a Graph...

92. A couple comments about
picking points on a Graph...
• Only use Integer coordinates. (No fractions or
decimals.)

93. A couple comments about
picking points on a Graph...
• Only use Integer coordinates. (No fractions or
decimals.)
• Never estimate coordinates. You may get lucky
but more often your equation is slightly off and
harder to find.

94. A couple comments about
picking points on a Graph...
• Only use Integer coordinates. (No fractions or
decimals.)
• Never estimate coordinates. You may get lucky
but more often your equation is slightly off and
harder to find.
• Try to use the x- and y-intercepts as your points.

95. Write the equation given 2 points
Write an equation in slope intercept
form of the line that passes through
(1, 2) and (4, -5).

96. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5).

97. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5).
y2 − y1
m=
x2 − x1

98. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

99. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

100. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

101. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1 • Substitute and simplify.

102. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 Will get the same slope.
m= =
x2 − x1 4 −1 • Substitute and simplify.

103. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.

104. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
• Use slope and one point to
find y-intercept. Choose the
“easier” point to work with.

105. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
• Use slope and one point to
find y-intercept. Choose the
“easier” point to work with.

106. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3

107. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
• Solve for b.

108. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3

109. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3
13
=b
3

110. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3 • Use the slope and y-intercept
13
=b
to write the equation in slope-
3 intercept form.

111. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3 • Use the slope and y-intercept
13
=b
to write the equation in slope-
3 intercept form.

112. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3 • Use the slope and y-intercept
13
=b
to write the equation in slope-
3 intercept form.

113. Write the equation given 2 points
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(1, 2) and (4, -5). • Label points as 1’s and 2’s.
( x1, y1 ) ( x2 , y2 ) Doesn’t matter which is which.
y2 − y1 −5 − 2 −7 Will get the same slope.
m= = =
x2 − x1 4 −1 3 • Substitute and simplify.
y = mx + b • Use slope and one point to
find y-intercept. Choose the
−7
2= ⋅1 + b “easier” point to work with.
3
7 −7 7 • Solve for b.
2+ = +b+
3 3 3 • Use the slope and y-intercept
13
=b 7 13 to write the equation in slope-
3 y=− x+ intercept form.
3 3

114. You try...
Write an equation in slope intercept
form of the line that passes through
(-3, 7) and (2, 4).

115. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4).

116. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4).
y2 − y1
m=
x2 − x1

117. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

118. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x1, y1 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

119. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1

120. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 Will get the same slope.
m=
x2 − x1 • Substitute and simplify.

121. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 Will get the same slope.
m= =
x2 − x1 −3 − 2 • Substitute and simplify.

122. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.

123. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
• Use slope and one point to
find y-intercept. Choose the
“easier” point to work with.

124. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
• Use slope and one point to
find y-intercept. Choose the
“easier” point to work with.

125. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5

126. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
• Solve for b.

127. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5

128. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5
6 6 6
4+ = − +b+
5 5 5

129. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5
6 6 6
4+ = − +b+
5 5 5
26
=b
5

130. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5
6 6 6 • Use the slope and y-intercept
4+ = − +b+
5 5 5 to write the equation in slope-
26 intercept form.
=b
5

131. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5
6 6 6 • Use the slope and y-intercept
4+ = − +b+
5 5 5 to write the equation in slope-
26 intercept form.
=b
5

132. You try...
Write an equation in slope intercept • Find the slope.
form of the line that passes through
(-3, 7) and (2, 4). • Label points as 1’s and 2’s.
( x2 , y2 ) ( x1, y1 ) Doesn’t matter which is which.
y2 − y1 7−4 3 Will get the same slope.
m= = =
x2 − x1 −3 − 2 −5 • Substitute and simplify.
y = mx + b • Use slope and one point to
3 find y-intercept. Choose the
4 = − ⋅2 + b “easier” point to work with.
5
6
4 = − +b • Solve for b.
5
6 6 6 • Use the slope and y-intercept
4+ = − +b+
5 5 5 to write the equation in slope-
3 26 intercept form.
26 y=− x+
=b 5 5
5

133. What does slope mean?

134. What does slope mean?
• It measures the steepness of a line.

135. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.

136. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.

137. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm

138. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm

139. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
• The “run” (purple arrow) is 100 miles. Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm

140. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
• The “run” (purple arrow) is 100 miles. Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm
• So we have -2 gallons/100 miles but both
numbers are even. Always simplify the
slope before determining what it means.

141. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
• The “run” (purple arrow) is 100 miles. Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm
• So we have -2 gallons/100 miles but both
numbers are even. Always simplify the
slope before determining what it means.
• Reduced the slope is -1 gallon/50 miles.

142. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
• The “run” (purple arrow) is 100 miles. Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm
• So we have -2 gallons/100 miles but both • When writing the meaning,
numbers are even. Always simplify the use some common sense to
slope before determining what it means. make a logical statement.
• Reduced the slope is -1 gallon/50 miles.

143. What does slope mean?
• It measures the steepness of a line.
• Also referred to as rate of change.
• Slope is the ratio rise/run.
• To find the “meaning” of slope, identify the
rise and run paying attention to the units.
• Here the “rise” (red arrow) is -2 gallons
because the line slopes downward and the
y-axis is in gallons.
• The “run” (purple arrow) is 100 miles. Image from http://regentsprep.org/REgents/math/ALGEBRA/AC1/Rate.htm
• So we have -2 gallons/100 miles but both • When writing the meaning,
numbers are even. Always simplify the use some common sense to
slope before determining what it means. make a logical statement.
• Reduced the slope is -1 gallon/50 miles. • For every 50 miles traveled
one gallon of gas is used.

144. You try...
Image from http://www.algebra-class.com/rate-of-change.html

145. You try...
What does the slope
represent in the graph to
the right?
Image from http://www.algebra-class.com/rate-of-change.html

146. You try...
What does the slope
represent in the graph to
the right?
• John’s savings account
balance increase $100
each month.
OR
Image from http://www.algebra-class.com/rate-of-change.html

147. You try...
What does the slope
represent in the graph to
the right?
• John’s savings account
balance increase $100
each month.
OR
• Every one month, John’s
savings account balance
increases by $100. Image from http://www.algebra-class.com/rate-of-change.html