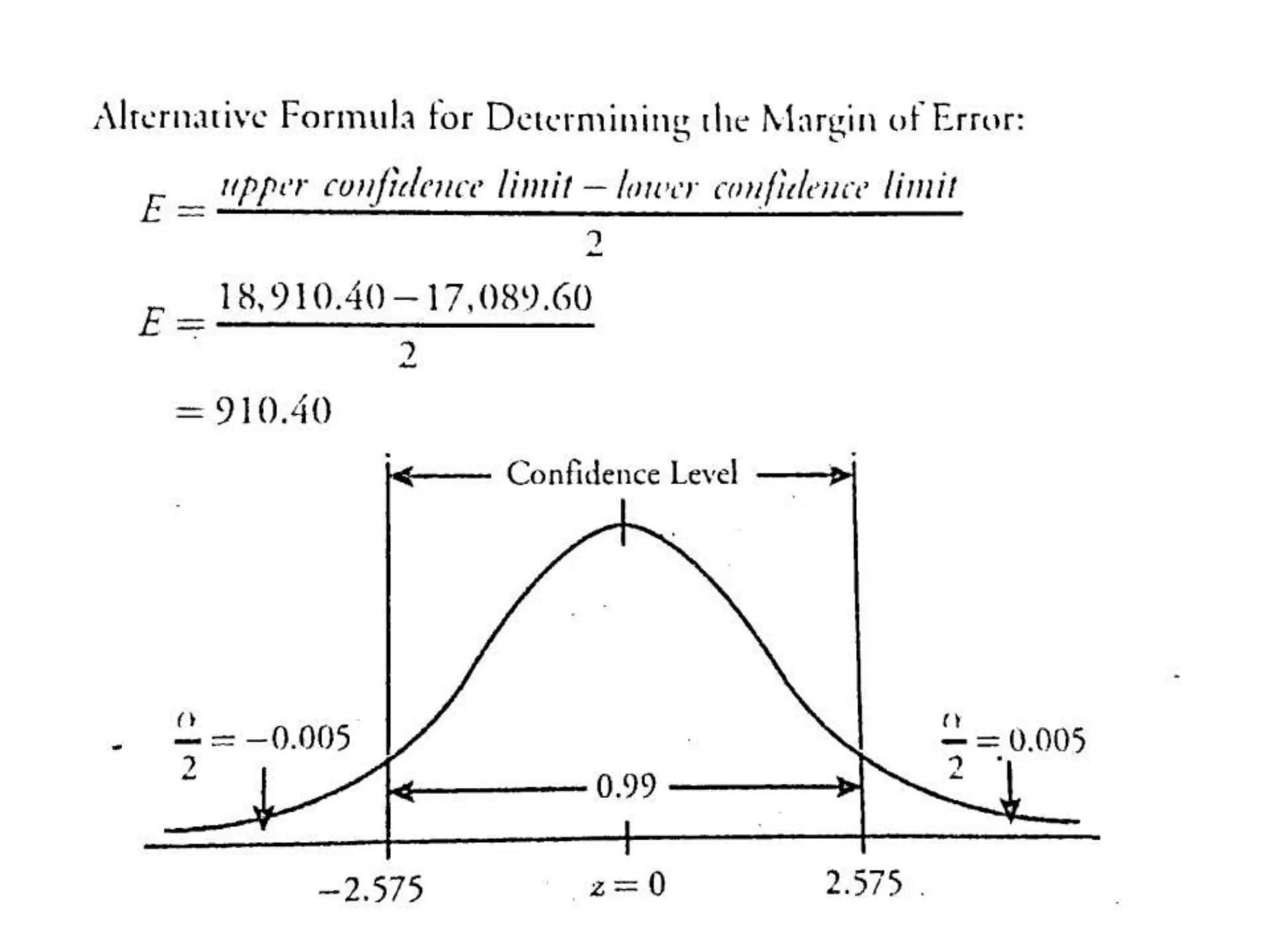
The document outlines the concepts of point and interval estimation in statistics, highlighting how to compute point estimates for population parameters, specifically the population mean. It explains the importance of random sampling and large sample sizes to improve the accuracy of estimations, as well as how to calculate confidence intervals to provide a range within which a population parameter is likely to lie. Several examples illustrate the application of these concepts, including the computation of confidence intervals for known population variances and sample means.