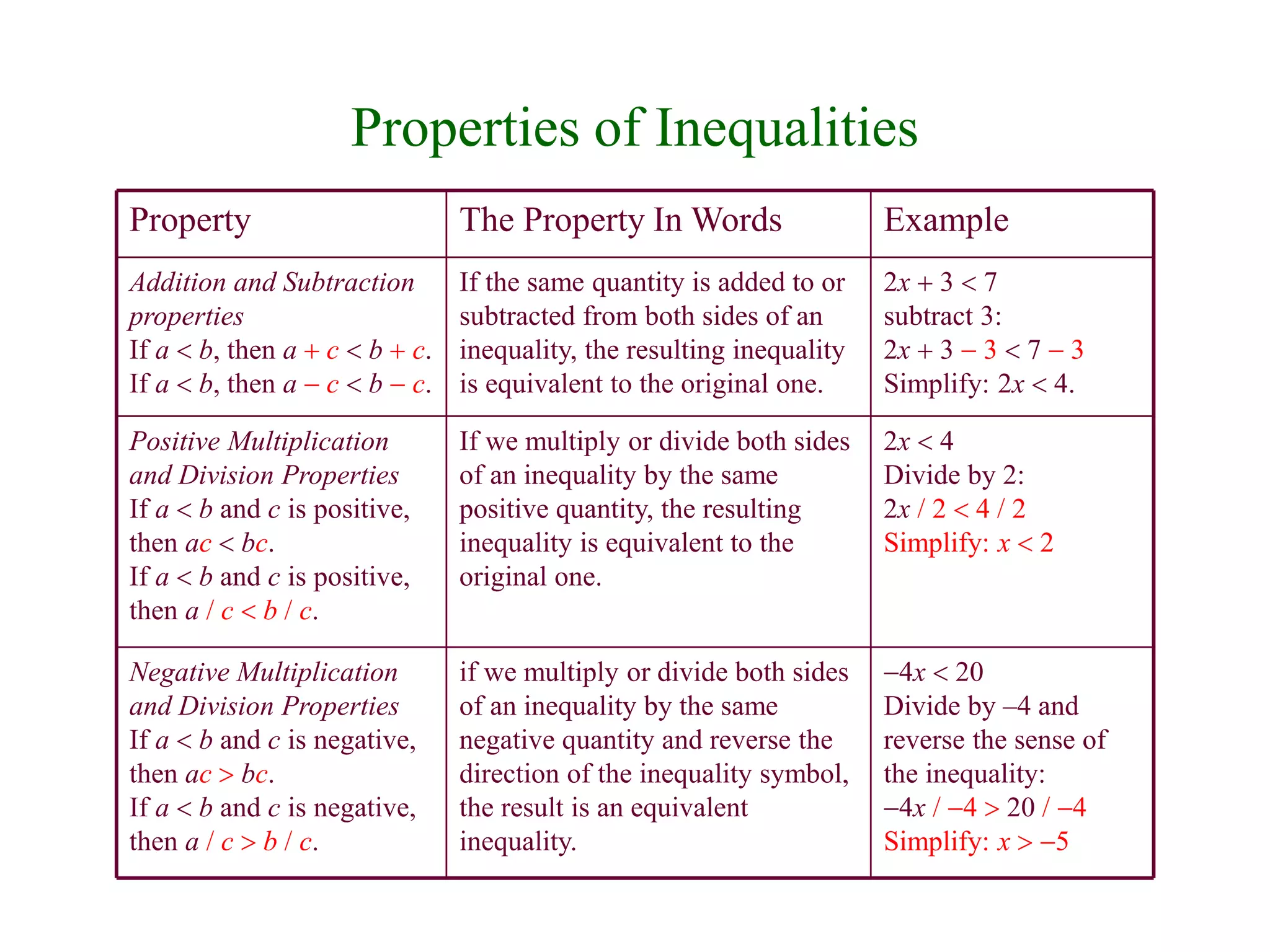
The document discusses graphs of linear inequalities on number lines. It explains that linear inequalities have solutions that can be represented by shading regions of the number line. It also summarizes properties of inequalities under multiplication, division, addition and subtraction. Examples are provided to demonstrate solving linear inequalities algebraically and graphing the solution sets on number lines with interval notation. Absolute value inequalities are also introduced, along with rules for determining the solutions from the absolute value expression.

1. Linear Inequalities

2. Graphs of Inequalities; Interval Notation
There are infinitely many solutions to the
inequality x > -4, namely all real numbers
that are greater than -4. Although we
cannot list all the solutions, we can make a
drawing on a number line that represents
these solutions. Such a drawing is called the
graph of the inequality.

3. Graphs of Inequalities; Interval Notation
• Graphs of solutions to linear inequalities
are shown on a number line by shading all
points representing numbers that are
solutions. Parentheses indicate endpoints
that are not solutions. Square brackets
indicate endpoints that are solutions.

4. Text Example
Graph the solutions of
a. x < 3 b. x  -1 c. -1< x  3.
Solution:
a. The solutions of x < 3 are all real numbers that are
less than 3. They are graphed on a number line by
shading all points to the left of 3. The parenthesis
at 3 indicates that 3 is not a solution, but numbers
such as 2.9999 and 2.6 are. The arrow shows that
the graph extends indefinitely to the left.
-5 -4 -3 -2 -1 0 1 2 3

5. Text Example cont.
Graph the solutions of
a. x < 3 b. x  -1 c. -1< x  3.
Solution:
b. The solutions of x  -1 are all real numbers that are
greater than or equal to -1. We shade all points to
the right of -1 and the point for -1 itself The
bracket at -1 shows that -1 is a solution for the
given inequality. The arrow shows that the graph
extends indefinitely to the right.
-5 -4 -3 -2 -1 0 1 2 3

6. Text Example cont.
Graph the solutions of
a. x < 3 b. x  -1 c. -1< x  3.
Solution:
c. The inequality -1< x  3 is read "-1 is less than x
and x is less than or equal to 3," or "x is greater
than -1 and less than or equal to 3." The solutions
of -1< x  3 are all real numbers between -1 and
3, not including -1 but including 3. The
parenthesis at -1 indicates that -1 is not a solution.
By contrast, the bracket at 3 shows that 3 is a
solution. Shading indicates the other solutions.
-5 -4 -3 -2 -1 0 1 2 3

7. Properties of Inequalities
Property The Property In Words Example
-4x < 20
Divide by –4 and
reverse the sense of
the inequality:
-4x  -4  20  -4
Simplify: x  -5
if we multiply or divide both sides
of an inequality by the same
negative quantity and reverse the
direction of the inequality symbol,
the result is an equivalent
inequality.
Negative Multiplication
and Division Properties
If a < b and c is negative,
then ac  bc.
If a < b and c is negative,
then a  c  b  c.
2x < 4
Divide by 2:
2x  2 < 4  2
Simplify: x < 2
If we multiply or divide both sides
of an inequality by the same
positive quantity, the resulting
inequality is equivalent to the
original one.
Positive Multiplication
and Division Properties
If a < b and c is positive,
then ac < bc.
If a < b and c is positive,
then a  c < b  c.
2x + 3 < 7
subtract 3:
2x + 3 - 3 < 7 - 3
Simplify: 2x < 4.
If the same quantity is added to or
subtracted from both sides of an
inequality, the resulting inequality
is equivalent to the original one.
Addition and Subtraction
properties
If a < b, then a + c < b + c.
If a < b, then a - c < b - c.

8. Example
Solve and graph the solution set on a number line:
4x + 5  9x - 10.
Solution We will collect variable terms on the left and constant terms on
the right.
4x + 5  9x - 10 This is the given inequality.
4x + 5 – 9x  9x - 10 - 9x Subtract 9x from both sides.
-5x + 5  -10 Simplify.
-5x + 5 - 5  -10 - 5 Subtract 5 from both sides.
-5x  -15 Simplify.
-5x/5 > -15/5 Divide both sides by -5 and reverse the sense
of the inequality.
x  3 Simplify.
The solution set consists of all real numbers that are greater than or equal to
3, expressed in interval notation as (-, 3]. The graph of the solution set is
shown as follows:

9. Solving an Absolute Value
Inequality
If X is an algebraic expression and c is a
positive number,
1. The solutions of |X| < c are the numbers that
satisfy -c < X < c.
2. The solutions of |X| > c are the numbers that
satisfy X < -c or X > c.
These rules are valid if < is replaced by  and
> is replaced by .

10. Text Example
Solve and graph: |x - 4| < 3.
Solution
|X| < c means -c < X < c
|x - 4| < 3 means -3< x - 4< 3
We solve the compound inequality by adding 4 to all
three parts.
-3 < x - 4 < 3
-3 + 4 < x - 4 + 4 < 3 + 4
1 < x < 7
The solution set is all real numbers greater than 1 and
less than 7, denoted by {x| 1 < x < 7} or (1, 7). The
graph of the solution set is shown as follows:

11. Linear Inequalities